Системы счисления

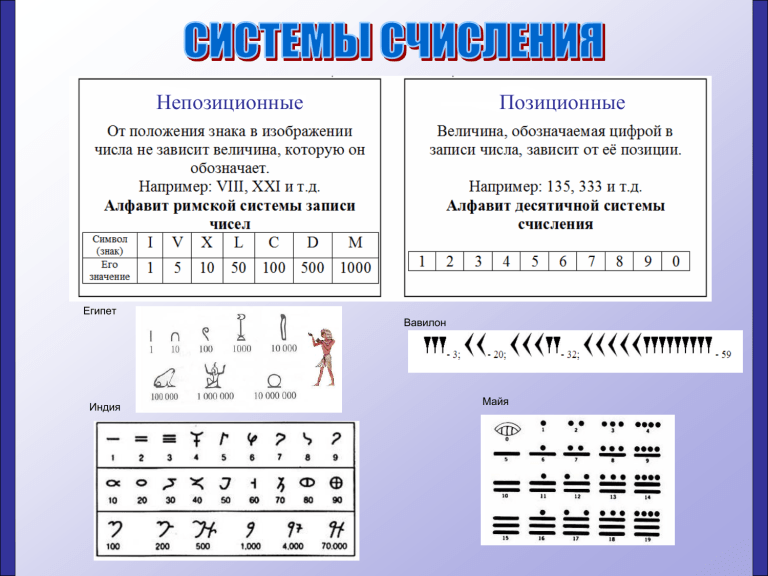
Непозиционные
Позиционные
Египет
Вавилон
Индия
Майя
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления — это количество различных знаков или символов,
используемых для изображения цифр в данной системе.
В настоящее время наиболее используемыми являются системы счисления:
Двоичная, восьмеричная и шестнадцатеричная системы удобны для компьютеров.
Недостаток двоичной системы – быстрый рост числа разрядов, необходимый для записи
чисел.
Примеры записи чисел в разных системах счисления:
Выбранное нами число в различных системах счисления может быть изображено с помощью
разных знаков, например, число 15 в десятичной системе соответствует 1111 в двоичной
системе, 17 в восьмеричной системе и F в шестнадцатеричной системе
Развернутая форма записи числа
В позиционной системе счисления любое вещественное число может быть представлено в виде:
где:
•
•
•
•
•
А
q
aI
n
m
– само число;
– основание системы счисления;
– цифры данной системы счисления
– число разрядов целой части числа;
– число разрядов дробной части числа.
Разряды
Число
2 10
-1
757,710= 7•102 + 5•101 + 7•100 + 7•10-1
2 10
3AF16= 3•162 + A•161 + F
Перевод чисел
из одной системы счисления
в другую
10 → 2 (целые числа)
Алгоритм перевода целых чисел
из десятичной системы счисления в
любую другую.
•
•
•
2510=110012
Последовательно выполнять деление данного
числа и получаемых целых частных на
основание новой системы до тех пор, пока не
получится частное, меньше делителя.
Получаемые остатки, являющиеся цифрами в
новой системе счисления, привести в
соответствие с алфавитом новой системы
счисления.
Составить число в новой системе, записывая
его, начиная с последнего остатка.
Перевести число из десятичной системы в двоичную:
124
2
-124 62
0 -62
246
2
2
-246 123 2
31 2
0 -122 61 2
0 -30 15 2
1 -60 30 2
1 -14 7 2
1 -30 15 2
1 -6 3 2
0 -14 7 2
1 -2 1
12410=11111002
1
1 -6 3 2
24610=111101102
1 -2 1
1
10 → 8 (целые числа)
Алгоритм перевода целых чисел
из десятичной системы счисления в
любую другую.
•
•
•
124
8
-120 15
8
4 -8
1
7
12410=1748
Последовательно выполнять деление данного
числа и получаемых целых частных на
основание новой системы до тех пор, пока не
получится частное, меньше делителя.
Получаемые остатки, являющиеся цифрами в
новой системе счисления, привести в
соответствие с алфавитом новой системы
счисления.
Составить число в новой системе, записывая
его, начиная с последнего остатка.
10 → 16 (целые числа)
Алгоритм перевода целых чисел
из десятичной системы счисления в
любую другую.
•
•
•
Последовательно выполнять деление данного
числа и получаемых целых частных на
основание новой системы до тех пор, пока не
получится частное, меньше делителя.
Получаемые остатки, являющиеся цифрами в
новой системе счисления, привести в
соответствие с алфавитом новой системы
счисления.
Составить число в новой системе, записывая
его, начиная с последнего остатка.
124
16
-112
7
12 = С
39310=18916
12410=7С16
10 → 2,8,16 (десятичная дробь)
Алгоритм перевода
Для того чтобы перевести правильную десятичную дробь из десятичной системы счисления в другую,
необходимо последовательно умножать эту дробь, а затем получаемые дробные части на основание той
системы, в которую она переводится.
Умножение производится до тех пор, пока дробная часть не станет равной нулю или не будет достигнута
требуемая точность. В новой системе дробь записывается в виде целых частей произведений, начиная с
первого.
Пример 2. Перевести число 0,6562510 в
Пример 1. Перевести число
Пример 3. Перевести число
восьмеричную систему счисления
0,532 из десятичной системы в
0,974 из десятичной системы в
двоичную с точностью до
шестнадцатеричную с точностью
тысячных.
до тысячных.
Решение: Последовательно
Решение: Последовательно
умножаем на 2 только дробную
умножаем на 16 только дробную
часть.
часть. 1510=F16
0|532
0|974
1|064
15|584
0|128
9|344
0|256
5|504
Ответ: 0,1002
Ответ: 0,F9516
Пример 1. Перевести число
344,532 из десятичной системы в
двоичную с точностью до
тысячных.
Решение: Переводим целую
часть числа. Получаем 34410
=1010110002. Переводим, с
указанной точностью, дробную
часть. Получаем 0,53210 = 0,1002
Дописываем после целой части
дробную: 344,53210
=101011000,1002.
Пример 2 Перевести число 153,2510 в
восьмеричную систему
Решение: Переводим целую
часть числа. Получаем
15310=2318
Для дробной части 0,2510=0,28
153,2510 =231,28
Пример 3. Перевести число
936,974 из десятичной системы в
шестнадцатеричную с точностью
до тысячных.
Решение: Переводим целую
часть числа. Получаем 93610 =
3A816. Переводим, с указанной
точностью, дробную часть.
Получаем 0,97410 = 0,F9516.
Дописываем после целой части
дробную: 936,97410 = 3A8,F9516.
Ответ: 3A8,F95 .
2,8,16 → 10
Алгоритм перевода чисел из любой системы счисления в
десятичную:
Представьте число в развернутой форме. При этом основание
системы счисления должно быть представлено в десятичной
системе счисления.
Найдите сумму ряда. Полученное число является значением
числа в десятичной системе счисления.
Перевести числа в десятичную систему:
10 -1
16,4 8=1*81+6*80+4*8-1=8+6+0.5=14.510
210
101 2=1*22+0*21 +1*20=4+0+1=510
210
110 2=1*22+1*21 +0*20=4+2+0=610
Перевести числа из восьмеричной в
двоичную систему:
8→2
2768
010 111 110
276 8=101111102
2 5, 024 8
010 101 000 010 100
25,024 8=10101,00001012
2 →8
Перевести числа из двоичной системы в
восьмеричную:
0,111 011 0112=0,7338
0
7
3
3
11 001 0102=3128
3
1
2
16 → 2
Перевести числа из шестнадцатеричной
в двоичную систему:
1 A C 7 16
0001 1010 1100 0111
1AC7 16=11010110001112
FA16
1111 1010
2 →16
FA16=111110102
Перевести числа из двоичной системы в
шестнадцатеричную:
0,1110 1101 10002=0,ED816
0
E
D
8
1100 1010 2=CA16
C
A
Арифметические операции
Основные арифметические операции в позиционных системах счисления
проводятся по тем же правилам, по которым они проводятся в десятичной
системе счисления.
Только таблицами сложения и умножения надо пользоваться особыми для
каждой системы.
Сложение ( Двоичная система )
Таблица сложения
0+0=0
0+1=1
1+0=1
1
1
=
1 + 1 = 10
Пример4
1102
+ 1012
1
10112
Пример5
Пример6
0102
10012
+ 0112
+ 00102
1
1012
10112
1
Вычитание ( Двоичная система )
Таблица вычитания
0<1, занимаем 1
0<1, нужно занять 1 в
предыдущих разрядах, но в
ближайших двух нули, поэтому
занимаем в старшем разряде,
где есть 1
в предыдущем разряде
10-1=1
в предыдущем разряде
10-1=1
так как занимали 1 в старшем
разряде, здесь осталась 1
10-1=1
1-1=0
1-1=0
от 1 остался 0
1-0=1
так как занимали 1 в старшем
разряде, здесь осталась 1
1-1=0
от 1 остался 0
1-0=1
1-1=0
0<1, занимаем 1
от 1 осталось 0,
занимаем 1 в старшем
разряде, где есть 1
10-1=1
занимали в старшем
разряде, поэтому
осталась 1
от 1 остался 0
Сложение ( Восьмеричная система )
Таблица сложения
=118
= 68
=128
= 78
305,408
+ 24,758
11
1
332,358
7+5=148
3+2+1=68
0+5=58
7+4=138
5+4+1=128
0+2+1=38
Вычитание ( Восьмеричная система )
Таблица сложения
4<5, занимаем 1 в предыдущем разряде
14-5=7
от 5 осталось 4, 4-0 =4
3<7, занимаем 1 в предыдущем разряде
13-7=4
от 6 осталось 5, 5-2=3
11
1
1
305,408
- 24,758
260,438
0<5, занимаем 1 в предыдущем разряде
6348
- 2758
3378
4<5, занимаем 1 в предыдущем разряде
8-5=3
8+4-5=7
от 4 осталось 3, 3< 7, занимаем 1 , 3+8-7 =4
от 3 осталось 2, 2< 7, занимаем 1 , 2+8-7 =3
от 5 осталось 4, 4-4=0
от 6 осталось 5, 5-2=3
0<2, занимаем 1 в предыдущем разряде
8-2=6
от 3 осталось 2
Сложение ( Шестнадцатеричная система )
Таблица сложения
293,8016
+ 3СС,9816
1 11
660,1816
0+8=8
8+9=11
3+С+1=10
9+С+1=16
2+3+1=6
Вычитание ( Шестнадцатеричная система)
Таблица сложения
C-8=4
9-7=2
1 1
1
3 A 4 E,516
- F C 4,F16
2 A 8 9,616
5<F, занимаем в
предыдущем разряде
15-F=6
E-1-4=9
4<C, занимаем в
предыдущем разряде
14-C=8
A<F, занимаем в
предыдущем разряде
19-F=A
от 3 осталось 2
Умножение ( Двоичная система)
Таблица умножения
0*0=0
0*1=0
=
1*0=0
1 *1 = 1
ПРИМЕРЫ:
010
* 011
------010
010
------110
Умножение (Восьмеричная система)
Таблица умножения
ПРИМЕРЫ:
163
* 63
-----531
1262
-------13351
Таблица сложения
1560,2
* 101,2
----------33404
15602
00000
15602
--------------160134,24
Умножение ( Шестнадцатеричная система )
Таблица умножения
Таблица сложения
ПРИМЕРЫ:
2F 16
* 15 16
----------E8
588
--------------332,А016
2С,416
* 12,816
----------1620
588
2С4
--------------332,А016
Кодирование информации
В большинстве современных компьютеров для хранения символа отводится 8-разрядная ячейка
(байт). В байт можно записать 256 различных двоичных чисел – это позволяет закодировать 256
разных символов.
Этого хватит, чтобы выразить различными комбинациями восьми битов все символы английского и
русского языков, как строчные, так и прописные, а также знаки препинания, символы основных
арифметических действий и некоторые общепринятые символы.
Для того, чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы
кодирования, а это пока невозможно из-за противоречий между символами национальных
алфавитов, а также противоречий корпоративного характера. Для английского языка эти
противоречия уже сняты.
Институт стандартизации США ввел в действие систему кодирования ASCII (American Standard Code
for Information Interchange – стандартный код информационного обмена США).
В ней закреплены две таблицы кодирования – базовая и расширенная. Базовая закрепляет значения
кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255.
Первые 32 кода базовой таблицы, начиная с нулевого, отданы производителям аппаратных средств
(в первую очередь производителям компьютеров и печатающих устройств).
В этой области размещаются так называемые управляющие коды, которым не соответствуют
никакие символы языков, и соответственно, эти коды не выводятся ни на экран, ни на устройство
печати.
В России широко используются две таблицы кодировки:
КОИ-8 (двоичный восьмибитовый Код Обмена Информацией)
Windows1251
Базовая таблица кодировки ASCII
Базовая таблица кодировки ASCII
Слово APPLE в кодировке ASCII будет выглядеть как : 65 80 80 76 69
Слово Irkutsk в кодировке ASCII будет выглядеть как : 73 114 107 117 116 115 107