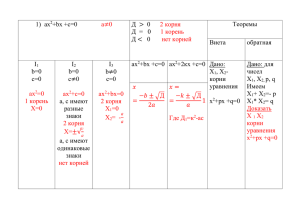
Формулы для справок. Арифметика и алгебра Пропорции 1. В пропорции пропорции а • d = b • с . а и d — крайние члены, b и c —средние. Основное свойство 2. Перестановка членов пропорции: 3. Производные пропорции: дана пропорция : Действия справедливы следующие пропорции со степенями Действия с корнями Корни предполагаются арифметическими. Квадратные уравнения 1. Уравнение вида x2 + px + q = 0 2. Уравнение вида ax2 + bx + c = 0 3. Уравнение вида ax2 + 2kx + c = 0 4. Если x1 и х2 — корни решается по решается решается уравнения x2 + px + q =(x—х1) (x—х2), где x1 6. ax2 + bx + c = а(x—х1) (x—х2), где x1 и и х2 — корни х2 — корни по формуле формуле x2 + px + q = 0 , x1 + х2 = —р и 5. по формуле тo x1 х2= q. уравнения x2 + px + q = 0 уравнения ax2 + bx + c = 0 Прогрессии (будет ссылка на раздел, когда доберемся до него) Логарифмы. Числа а (основание логарифма) и N предполагаются положительными, причем а отлично от 1. 1. Запись loga N = х равнозначна записи ах = N так что имеем тождество 8. O модуле перехода от системы логарифмов с основанием b к системе с основанием а ... разговор пойдет в соответствующем разделе, а здесь будет дана ссылка на него. Впрочем, если очень интересно, то можно посмотреть уже сейчас здесь Соединения Бином Ньютона 2. Общий член разложения: a⁴-b⁴ = (a²-b²)(a²+b²) = (a-b)(a+b)(a²+b²) a⁶-b⁶ = (a³-b³)(a³+b³) = (a-b)(a²+ab+b²)(a+b)(a²ab+b²) a⁸-b⁸ = (a⁴-b⁴)(a⁴+b⁴) = (a²b²)(a²+b²)(a⁴+b⁴)=(a-b)(a+b)(a²+b²)(a⁴+b