Тема
реклама

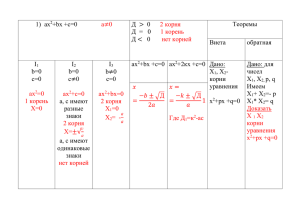
МБОУ Проволоченская основная общеобразовательная школа Организация активной самостоятельной деятельности обучающихся средствами проблемного обучения РМО учителей математики Подготовила: учитель физики математики Боброва Надежда Сергеевна категория: высшая р.п. Виля 2014 г. и Говорят уравнение вызывает сомнение, но итогом сомнения может быть озарение! Как же создавать проблемные ситуации? 28k + 30n + 31m = 365 Задание: Найти хотя бы одно решение уравнения. Качество образования определяется его функциональностью, способностью ученика применять свои знания при решении практических проблем. Если выпускник имеет знания, но не может их применить, не может решать проблемы практической деятельности, то его образование некачественное. В условиях введения новых стандартов смысловым ориентиром становится развитие личности ребенка, а не «получение знаний». Это в корне меняет целевые ориентиры деятельности. Приоритетным становятся: достижение и поддержание высокого уровня мотивации ребенка к образованию; достижение уровня знаний, необходимых и достаточных для следующей ступени образования, обеспечивающего компетентностное освоение и решение (на уровне самостоятельной деятельности) задач учебной и социальной направленности; достижение самостоятельности в учебной и социально направленной деятельности, рефлексивной оценке и самооценке результатов. Основная проблема, связанная с изучением и введением нового стандарта — научить учителя строить новые взаимоотношения между детьми, партнерские отношения между учителем и ребенком. Роль учителя — создать условия, чтобы дети добывали знания в процессе познавательной, исследовательской деятельности, в работе над заданиями, непосредственно связанными с проблемами реальной жизни. Наряду с традиционным вопросом «ЧЕМУ УЧИТЬ?», учитель должен понимать: как учить, чтобы у детей возникали собственные вопросы «ЧЕМУ МНЕ НАДО 2 НАУЧИТЬСЯ?» Ребенок должен стать «архитектором «образовательного процесса». Каким образом это происходит в процессе организации активной самостоятельной деятельности ? Немного теории: Активность (учения, освоения, содержания и т.п.) определяет степень (интенсивность, прочность) «соприкосновения» обучаемого с предметом его деятельности. В структуре активности выделяются следующие компоненты: - готовность выполнять учебные задания; - стремление к самостоятельной деятельности; - сознательность выполнения заданий; - систематичность обучения; - стремление повысить свой личный уровень и другие. С активностью непосредственно сопрягается еще одна важная сторона мотивации учения учащихся это самостоятельность, которая связана с определением объекта, средств деятельности, её осуществления самим учащимся без помощи взрослых и учителей. Познавательная активность и самостоятельность неотделимы друг от друга: более активные школьники, как правило, и более самостоятельные; недостаточная собственная активность учащегося ставит его в зависимость от других и лишает самостоятельности. Управление активностью учащихся традиционно называют активизацией. Активизацию можно определить как постоянно текущий процесс побуждения учащихся к энергичному, целенаправленному учению, преодоление пассивной и стерео типичной деятельности, спада и застоя в умственной работе. Главная цель активизации – формирование активности учащихся, повышение качества учебновоспитательного процесса. В педагогической практике используются различные пути активизации деятельности, основные среди них – разнообразие форм, методов, средств 3 обучения, выбор таких их сочетаний, которые в возникших ситуациях стимулируют активность и самостоятельность учащихся. Наибольший активизирующий эффект на занятиях дают ситуации, в которых учащиеся сами должны: отстаивать свое мнение; принимать участие в дискуссиях и обсуждениях; самостоятельно ставить вопросы; рецензировать ответы отвечающих; оценивать ответы и письменные работы товарищей; самостоятельно выбирать посильное задание; находить несколько вариантов возможного решения познавательной задачи (проблемы); создавать ситуации самопроверки, анализа личных познавательных и практических действий; решать познавательные задачи путем комплексного применения известных им способов решения. Можно утверждать, что новые технологии самостоятельного обучения имеют в виду, прежде всего повышение активности учащихся: истина добытая путем собственного напряжения усилий, имеет огромную познавательную ценность. Считаю, что для активизации самостоятельной деятельности учащихся целесообразно использовать проблемные ситуации. Анализируя проблемную ситуацию, поставленную учителем, учащийся как правило, должен не только найти способ решения заключённой в ней проблемы, но и провести определённое обобщение этой ситуации или сравнить с какой-либо другой ситуацией, т.е. видеть за данной проблемой новую проблему, которую можно и целесообразно было бы изучить. Для того, чтобы проблемное обучение способствовало формированию и развитию способности к творческой деятельности и потребности в ней, я 4 включаю в процесс обучения совокупность и систему проблемных задач и учебных проблем на различных этапах урока. Проблемная организация этапа ознакомление с новым учебным материалом предполагает, что он должен состоять из следующих элементов: создание проблемной ситуации; включение учащихся в проблемную ситуацию и постановка (формулирование) учебной цели; решение проблемы; анализ, обобщение и оценка работы по решению проблемы и осуществлению учебной цели. Проблемные ситуации в данном случае могут быть двух типов: познавательные и исследовательские. Познавательные проблемные ситуации для первичного ознакомления с новым учебным материалом могут быть созданы разными приемами: рассказом учителя о практической или теоретической роли изучаемого явления, процесса, события или понятия, закономерности; рассказом об истории научного открытия того понятия или закономерности, которое будет изучаться; постановкой перед учащимися практической или теоретической задачи, для решения которой необходимо изучение предстоящей темы и т. д. Приведу примеры задач, которые способствуют созданию проблемной ситуации: Пример 1. Проблемное введение в тему «Наименьшее общее кратное» «Таня купила в магазине яйца и положила их в небольшую корзиночку. По дороге домой она сообразила, что число купленных яиц делится без остатка и на 2, и на 3, и на 5, и на 10, и на 15. Сколько же яиц несла Таня домой?» Обязательно найдется ученик, который предложит следующее решение : «Чтобы найти число яиц, надо перемножить числа 2,3,5,10,15. Получится 4500 яиц. Разве может поместиться столько яиц в одной корзиночке?» После обсуждения этого решения ребята приходят к выводу: ошибка заключается в том, что ученик перемножил все данные числа. А ведь можно 5 найти значительно меньшее Возникает вопрос: какое? число, обладающее указанным свойством. «Наименьшее общее кратное» Пример 2. Тема: «Формулы сокращённого умножения» 7 кл. Преступники украли в банке большую сумму денег. Их поймали, но похищенную сумму установить не удалось. Преступники категорически отказываются назвать её, утверждая, что записали это число в виде степени и зашифровали не только основание, но и её показатель. Экспертам удалось узнать основание степени. Это число 597. Но каким был показатель не говорят. После очередного допроса преступники сказали, что показатель степени является корнем уравнения ( 2y +1)2 – 4y2 =9 y=2 5972 = (600 – 3)2 =6002 -2 х 600 х 3 + 32 = 360000 – 3600 + 9 =356409 Пример3. Тема: «Формула корней квадратного уравнения» Вы знаете, что математика одна из древнейших наук. В Древней Индии были распространены публичные соревнования по решению трудных задач. Задачи часто представлялись в стихотворной форме. Вот одна из таких задач: Обезьянок резвых стая Всласть, поевши, развлекалась. Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам Стали прыгать, повисая… Сколько ж было обезьянок, Ты скажи мне, в этой стае? Далее по тексту задачи составляется уравнение. При этом учащиеся могут допустить сами или учитель может спровоцировать следующую ошибку: . После проверки окончательно получаем уравнение . 6 Это уравнение вида ax2 + bx + c = 0. Далее выясняется. Почему оно называется квадратным, являются ли квадратными уравнения вида ax2 + bx = 0, ax2 + c = 0, bx + c = 0. Возникает проблема, как решать такие уравнения? Затем рассматриваются предлагаемые учащимся пути решения неполных квадратных уравнений, предпринимаются безуспешные попытки решения полного уравнения , записанного в общем виде ax2 + bx + c = 0. Вынесение общего множителя x (ax + b) + c = 0 по аналогии с решением уравнения ax2 + bx = 0, или перенос свободного члена ax2 + bx = – c по аналогии с уравнением ax2 + c = 0 не приносят желаемых результатов. Все попытки решения обсуждаются. Если ученики высказывают сомнение можно ли решить эту задачу вообще, учитель предъявляет им уравнение , которое ребята способны решить и в котором после проведённых преобразований «узнают» исходное уравнение. Пример 4. Тема: «Теорема Виета» Уравнение Корни Произведение корней Сумма корней 5 и-3 -15 2 4 и-7 -28 -3 6и8 48 14 -12 и-3 36 -15 х1 и х2 ? ? Пример 5. Например, перед изучением темы «Формула суммы n первых членов арифметической прогрессии» предполагаю решить задачу: Вагонная рессора состоит из 10 металлических листов, наложенных друг на друга и сшитых. Верхний лист рессоры имеет длину 105 см, а каждый из остальных на 9 7 см короче предыдущего. Найти общую длину десяти металлических листов, необходимых для изготовления рессоры. Учащиеся пытаются составить арифметическую прогрессию и найти ее сумму. Но видят, что это громоздкая работа. Обнаруживается недостаточность ранее усвоенных знаний, т.е. происходит рефлексия, возникает необходимость в получении, в выводе новой формулы. Пример 6. Перед выводом формулы суммы n членов геометрической прогрессии ученикам предлагается, например, такая жизненная ситуация. Однажды незнакомец постучал в окно к богатому купцу и предложил такую сделку: « Я буду ежедневно в течение 30 дней приносить тебе по 100 000 руб. А ты мне в первый день за 100 000 руб. дашь 1коп., во второй день за 100 000 руб. – 2 коп. и так каждый день будешь увеличивать предыдущее число денег в 2 раза. Если тебе выгодна сделка, то с завтрашнего дня начнем». Купец обрадовался такой удаче. Он подсчитал, что за 30 дней получит от незнакомца 3 000 000 руб. На следующий день пошли к нотариусу и узаконили сделку. Создается проблемная ситуация. Кто в этой сделке проиграл: купец или незнакомец? Учащиеся составляют последовательность чисел: 1; 2; 4; 8; 16; 32; 64; 128; 256; … Убеждаются, что эти числа составляют геометрическую прогрессию со знаменателем q = 2, первым членом a1 = 1 и количеством членов n = 30. Большинство школьников стремятся составить всю последовательность, чтобы потом найти ее сумму. Но видят, что это громоздкая работа, которая требует времени. Обращаются с вопросом : «Возможно ли вывести формулу n членов геометрической прогрессии в общем виде?» можно усилить проблемность, рассказывая историю о награде изобретателя шахматной игры: «По преданию, индийский принц Сирам, восхищенный остроумием игры и разнообразием возможных положений шахматных фигур, призвал к себе ее изобретателя, ученого Сету, и сказал ему: «Я желаю достойно вознаградить тебя за прекрасную игру, которую ты придумал. Я достаточно богат, чтобы исполнить любое твое желание». Сета попросил принца положить на первую 8 клетку шахматной доски 1 пшеничное зерно, на вторую два зерна, на третью – 4 зерна и т.д. Возникает необходимость найти S64 , где a1 = 1, q = 2, n = 64. Под руководством учителя учащиеся выводят формулу .Убеждаются, что купец проиграл. Пример7. Тема «Длина окружности» 5кл. Ещё древние греки находили длину окружности по формуле C = П*d. d – диаметр окружности. Вопрос : что же такое П? 1.Опоясать стакан ниткой, распрямить нитку, длина нитки примерно равна длине окружности стакана. Чтобы получить более точный результат, нужно это проделать несколько раз. Занесите данные в следующую таблицу: 2. Измерьте диаметр стакана линейкой. Данные занесите в табл. 3. Найдите значение П, как неизвестного множителя. Исследование проведено. Проблема решена. А для запоминания большего числа знаков существуют забавные поговорки и стихи. Например, такие: Нужно только постараться И запомнить всё как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. С.Бобров. ”Волшебный двурог” Тот, кто выучит это четверостишие, всегда сможет назвать 8 знаков числа : 3,1415926… Пример 8. Тема: «Теорема Пифагора» Учитель предлагает решить задачу: На охоте с двух отвесных скал два охотника заметили козла и одновременно в него выстрелили, причём стрелы достигли цели одновременно. Охотники одновременно начали спуск к добыче с одинаковой скоростью (см. рис. 3). Рисунок 3 9 Проблемная ситуация возникает при построении математической модели практической задачи. Она рассматривается с помощью вопросов. Как на чертеже изображаются: 1) скалы? 2) расстояние между ними? 3) путь каждой стрелы? 4) путь каждого охотника? 5) что означает факт, что стрелы достигли цели одновременно? Анализ задачи позволяет заключить, что на данном этапе задачу решить нельзя, так как невозможно использовать равенство отрезков ДС и СЕ, которые являются гипотенузами прямоугольных треугольников. Если бы зависимость между катетами и гипотенузой в прямоугольном треугольнике была известной, то можно было бы в каждом треугольнике выразить гипотенузу через катеты и приравнять полученные выражения. ВОЗНИКАЕТ ПРОБЛЕМА: Существует ли зависимость между гипотенузой и катетами в прямоугольном треугольнике, и, если она существует, то как она формулируется? Для решения этой проблемы учитель организует поиск формулировки, предложив учащимся задание по группам: Построить прямоугольные треугольники с катетами 3 и 4, 12 и 5, 6 и 8, 8 и 15 и измерить гипотенузу. Результаты заносятся в таблицу. Далее выдвигаются и обсуждаются различные гипотезы. Верно ли, что a + , если это справедливо для первого и третьего случая? Верно ли, что a = , если это справедливо для четвёртого случая? Если учащиеся не увидят существующей зависимости, то учитель продолжает заполнять таблицу, находя квадраты соответствующих значений. Следующая проблема возникает при доказательстве. Можно использовать различные доказательства, известные из истории математики. После 10 доказательства теоремы Пифагора, возвращаемся к исходной задаче. В заключении этого урока можно предложить учащимся следующий вопрос: В Древнем Египте после разлива Нила требовалось восстановить границы земельных участков, для чего на местности необходимо было строить прямые углы. Египтяне поступали следующим образом: брали верёвку , завязывали на равных расстояниях узлы и строили треугольники со сторонами 3,4 и 5 таких отрезков. Правильно ли они поступали? Далее следует построение математической модели, формулировка проблемы и поиск доказательства. Проблемное обучение включает в себя не только постановку вводной задачи, создания проблемной ситуации, но и, в отличие от традиционного преподавания, побуждает учащихся к самостоятельной, исследовательской работе над данной ситуацией, к открытию новых свойств, обоснованию всех своих рассуждений. Исследовательские проблемные ситуации создаются теми же способами, что и познавательные, отличие от последних состоит в том, что постановка проблемы у них иная. Если познавательная проблема состоит в том, что бы познать что-то, рассмотреть и выяснить что-то, то исследовательская проблема состоит в установлении причины, почему происходит то или иное явление, как разрешить видимое противоречие и что для этого нужно сделать и т. д. Пример 9. Сталкивает противоречия практической деятельности Побуждение к осознанию противоречия осуществляется репликами: «Вы смогли выполнить задание? В чем затруднение? «Почему так получилось? Чего мы еще не знаем?». Тема:«Построение треугольника по трем элементам. Неравенство треугольника» Построить с помощью циркуля и линейки треугольник со сторонами: а) 5см; 6см; 7см; б) 9см; 5см; 6см; в) 1см; 2см; 3см; 11 г) 3см; 4см; 10см. Тема: «Сумма внутренних углов треугольника» Перед изучением темы о сумме углов треугольника предлагаю такую задачу- проблему: “Построить треугольник по трём заданным углам: а) А = 90°, В = 60°, С = 45°; б) А = 70°, В = 30°, С = 50°; в) А = 50°, В = 60°, С = 70°. После решения этой задачи учащиеся сами делают вывод. Для поддержания интереса во время решения проблемной ситуации важно форма организации урока: урок-расследование, путешествие, урокаукцион, конференция и т.д. Создание проблемных ситуаций на уроках математики не только формирует ту систему математических знаний, умений и навыков, которая предусмотрена программой, но и самым естественным образом развивает у школьников творческую активность. Ситуация затруднения школьника в решении задач приводит к пониманию учеником недостаточности имеющихся у него знаний, что в свою очередь вызывает интерес к познанию и установку на приобретение новых. Нельзя заставлять ребёнка слепо штудировать предмет в погоне за общей успеваемостью. Необходимо давать ему возможность экспериментировать и не бояться ошибок, воспитывать у учащихся смелость быть не согласным с учителем. Всякий раз при разрешении проблемной ситуации я с удовольствием наблюдаю, как ребята не только усваивают новое для себя, но и переживают этот процесс как «открытие» ещё чего-то неизвестного. 12