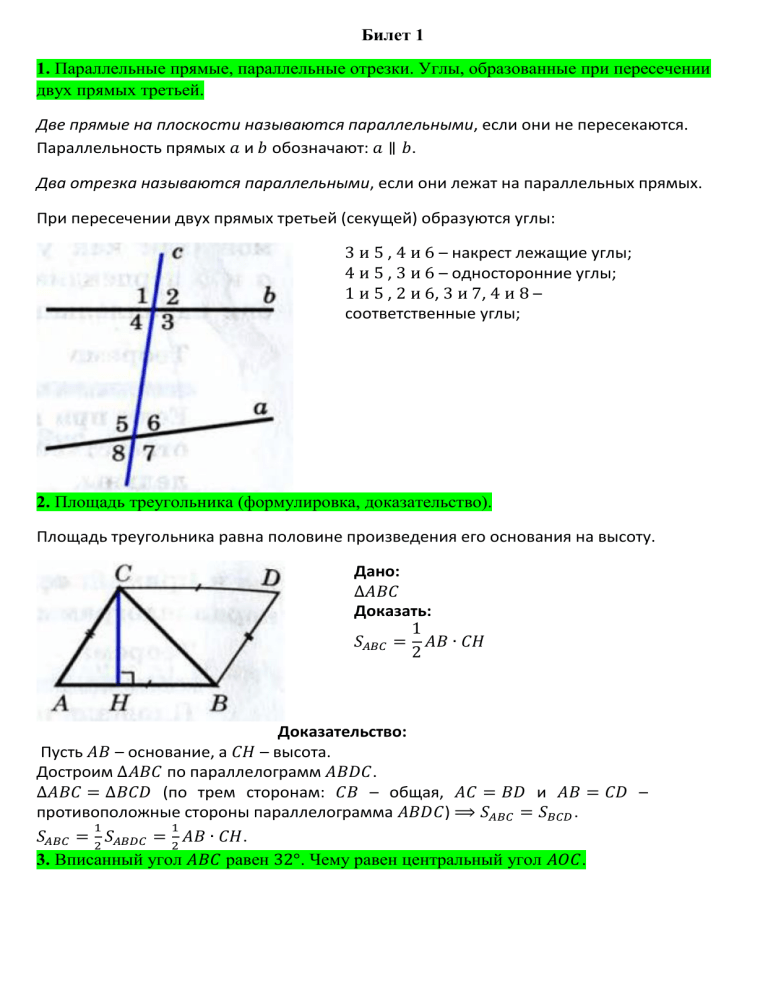
Билет 1 1. Параллельные прямые, параллельные отрезки. Углы, образованные при пересечении двух прямых третьей. Две прямые на плоскости называются параллельными, если они не пересекаются. Параллельность прямых 𝑎 и 𝑏 обозначают: 𝑎 ∥ 𝑏. Два отрезка называются параллельными, если они лежат на параллельных прямых. При пересечении двух прямых третьей (секущей) образуются углы: 3 и 5 , 4 и 6 – накрест лежащие углы; 4 и 5 , 3 и 6 – односторонние углы; 1 и 5 , 2 и 6, 3 и 7, 4 и 8 – соответственные углы; 2. Площадь треугольника (формулировка, доказательство). Площадь треугольника равна половине произведения его основания на высоту. Дано: ∆𝐴𝐵𝐶 Доказать: 1 𝑆𝐴𝐵𝐶 = 𝐴𝐵 ∙ 𝐶𝐻 2 Доказательство: Пусть 𝐴𝐵 – основание, а 𝐶𝐻 – высота. Достроим ∆𝐴𝐵𝐶 по параллелограмм 𝐴𝐵𝐷𝐶. ∆𝐴𝐵𝐶 = ∆𝐵𝐶𝐷 (по трем сторонам: 𝐶𝐵 – общая, 𝐴𝐶 = 𝐵𝐷 и 𝐴𝐵 = 𝐶𝐷 – противоположные стороны параллелограмма 𝐴𝐵𝐷𝐶) ⟹ 𝑆𝐴𝐵𝐶 = 𝑆𝐵𝐶𝐷 . 1 1 𝑆𝐴𝐵𝐶 = 𝑆𝐴𝐵𝐷𝐶 = 𝐴𝐵 ∙ 𝐶𝐻. 2 2 3. Вписанный угол 𝐴𝐵𝐶 равен 32°. Чему равен центральный угол 𝐴𝑂𝐶. Билет 2 1. Медиана, биссектриса и высота треугольника. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Любой треугольник имеет три медианы. Свойство: Медианы треугольника пересекаются в одной точке. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точной противоположной стороны, называется биссектрисой треугольника. Любой треугольник имеет три биссектрисы. Свойство: Биссектрисы треугольника пересекаются в одной точке. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника. Любой треугольник имеет три биссектрисы. Свойство: Высоты треугольника или их продолжения пересекаются в одной точке. 2. Теорема о биссектрисе угла (формулировка, доказательство). 1) Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. 2) ОБРАТНО: каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе. Дано: ∠𝐵𝐴C 1) 𝐴𝑀 – биссектриса. 2) 𝑀 – равноудалена от сторон ∠𝐵𝐴𝐶. Доказать: 1) 𝑀 – равноудалена от сторон ∠𝐵𝐴𝐶. 2) 𝐴𝑀 – биссектриса. Доказательство: 1) Проведем перпендикуляры 𝑀𝐾 и 𝑀𝐿 к прямым 𝐴𝐵 и 𝐴𝐶. ∆𝐴𝐾𝑀 = ∆𝐴𝐿𝑀 – прямоугольные (по гипотенузе и острому углу: 𝐴𝑀 – общая, ∠1 = ∠2 так как 𝐴𝑀 биссектриса) ⇒ 𝐾𝑀 = 𝑀𝐿, а значит, 𝑀 – равноудалена от сторон ∠𝐵𝐴𝐶. 2) Проведем перпендикуляры 𝑀𝐾 и 𝑀𝐿 к прямым 𝐴𝐵 и 𝐴𝐶. ∆𝐴𝐾𝑀 = ∆𝐴𝐿𝑀 – прямоугольные (по гипотенузе и катету: 𝐴𝑀 – общая, 𝑀𝐾 = 𝑀𝐿 по условию) ⇒ ∠1 = ∠2, а значит, 𝐴𝑀 – биссектриса. 3. Средняя линия 𝐾𝑀 треугольника 𝐴𝐵𝐶 отсекает от него треугольник 𝑀𝐵𝐾, площадь которого равна 10 см². Найдите площадь треугольника 𝐴𝐵𝐶. Билет 3 1. Определение прямоугольника и его свойства. Прямоугольник – параллелограмм, у которого все углы прямые. Свойства: 1) Противоположные стороны прямоугольника равны. 2) Диагонали прямоугольника точкой пересечения делятся пополам. 3) Диагонали прямоугольника равны. 2. Свойства равнобедренного треугольника. Доказательство одного из свойств равнобедренного треугольника. 1) в равнобедренном треугольнике углы при основании равны. Дано: ∆𝐴𝐵𝐶 – равнобедренный, 𝐵𝐶 – основание. Доказать: ∠𝐵 = ∠𝐶 Доказательство: Пусть 𝐴𝐷 – биссектриса ∆𝐴𝐵𝐶. ∆𝐴𝐵𝐷 = ∆𝐴𝐶𝐷 (по двум сторонам и углу между ними: 𝐴𝐵 = 𝐴𝐶 по условию, 𝐴𝐷 – общая, ∠1 = ∠2 - 𝐴𝐷 – биссектриса ∆𝐴𝐵𝐶) ⇒ ∠𝐵 = ∠𝐶. 2) В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Дано: ∆𝐴𝐵𝐶 – равнобедренный, 𝐵𝐶 – основание. 𝐴𝐷 - биссектриса Доказать: 𝐴𝐷 – медиана, 𝐴𝐷 – высота. Доказательство: ∆𝐴𝐵𝐷 = ∆𝐴𝐶𝐷 (по двум сторонам и углу между ними: 𝐴𝐵 = 𝐴𝐶 по условию, 𝐴𝐷 – общая, ∠1 = ∠2 - 𝐴𝐷 – биссектриса ∆𝐴𝐵𝐶) ⇒ 𝐵𝐷 = 𝐶𝐷, а значит, 𝐴𝐷 – медиана. ∠3 и ∠4 – смежные и ∠3 = ∠4 ⇒ ∠3 = 180° ∶ 2 = 90°, а значит, 𝐴𝐷 – высота. 3. Катеты прямоугольного треугольника 6 и 8 см. Вычислите высоту, проведенную к гипотенузе. Билет 4 1. Пропорциональные отрезки в прямоугольном треугольнике. Отрезок 𝑋𝑌 называется средним пропорциональным (или средним геометрическим) для отрезков 𝐴𝐵 и 𝐶𝐷, если 𝑋𝑌 = √𝐴𝐵 ∙ 𝐶𝐷. 1) Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой. 𝐶𝐷 = √𝐴𝐷 ∙ 𝐷𝐵 2) Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и гипотенузой, проведённой из вершины прямого угла. 𝐴𝐶 = √𝐴𝐵 ∙ 𝐴𝐷 или 𝐵𝐶 = √𝐴𝐵 ∙ 𝐶𝐵 2. Площадь параллелограмма (формулировка, доказательство). Площадь параллелограмма равна произведению его основания на высоту. Дано: 𝐴𝐵𝐶𝐷 – параллелограмм. 𝐴𝐷 – основание, 𝐵𝐻 – высота. Доказать: 𝑆𝐴𝐵𝐶𝐷 = 𝐴𝐷 ∙ 𝐵𝐻 Доказательство: Проведем высоту 𝐶𝐾. 𝑆𝐴𝐵𝐶𝐾 = 𝑆𝐴𝐵𝐻 + 𝑆𝐻𝐵𝐶𝐾 = 𝑆𝐴𝐵𝐶𝐷 + 𝑆𝐶𝐷𝐾 . ∆𝐴𝐵𝐻 = ∆𝐶𝐷𝐾 – прямоугольные (по гипотенузе и острому углу: 𝐴𝐵 = 𝐶𝐷 – противолежащие стороны параллелограмма 𝐴𝐵𝐶𝐷, ∠1 = ∠2 – соответственные при 𝐴𝐵 ∥ 𝐶𝐷 и секущей 𝐴𝐾) ⇒ 𝑆𝐴𝐵𝐶𝐷 = 𝑆𝐵𝐻𝐾𝐶 = 𝐴𝐷 ∙ 𝐵𝐻. 3. Найдите сторону равностороннего треугольника, если его высота равна 3. Билет 5 1. Смежные и вертикальные углы. Перпендикулярные прямые. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла. Две прямые, перпендикулярные третьей, не пересекаются. 2. Теорема Пифагора (формулировка, доказательство). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Дано: Прямоугольный треугольник. 𝑎, 𝑏 – катеты, 𝑐 – гипотенуза. Доказать: 𝑐 2 = 𝑎2 + 𝑏 2 Доказательство: Достроим треугольник до квадрата со стороной 𝑎 + +𝑏. Площадь 𝑆 этого квадрата равна (𝑎 + 𝑏)2 . 1 Так же этот квадрат состоит из 4 равных треугольников, с площадью 𝑎𝑏 и квадрата со 2 стороной 𝑐 и площадью 𝑐 2 . Поэтому, 1 (𝑎 + 𝑏)2 = 4 ∙ 𝑎𝑏 + 𝑐 2 2 𝑎2 + 2𝑎𝑏 + 𝑏 2 = 2𝑎𝑏 + 𝑐 2 𝑐 2 = 𝑎2 + 𝑏 2 3. Найдите углы, образованные двумя пересекающимися прямыми, если один из углов равен 50°. Билет 6 1. Определение вписанной окружности и ее свойства. Если все стороны многоугольника касаются окружности, то окружность называется вписанной, а многоугольник – описанным около этой окружности. Теорема. В любой треугольник можно вписать окружность. Свойства: 1) В треугольник можно вписать только одну окружность. 2) Площадь треугольника равна произведению его полупериметра на радиус 1 вписанной в него окружности 𝑆 = 𝑝𝑟. 2 3) В любом описанном четырехугольник суммы противоположных сторон равны. 4) Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. 2. Площадь трапеции (формулировка, доказательство). Площадь трапеции равна произведению полусуммы ее оснований на высоту. Дано: 𝐴𝐵𝐶𝐷 – трапеция 𝐵𝐻 - высота Доказать: 𝐴𝐷 + 𝐵𝐶 𝑆= ∙ 𝐵𝐻 2 Доказательство: Диагональ 𝐵𝐷 разделяет трапецию 𝐴𝐵𝐶𝐷 на два треугольника 𝐴𝐵𝐷 и 𝐵𝐶𝐷 ⇒ 𝑆𝐴𝐵𝐶𝐷 = 𝑆𝐴𝐵𝐷 + 𝑆𝐵𝐶𝐷 . 1 Пусть 𝐵𝐻 – высота, а 𝐴𝐷 – основание ∆𝐴𝐵𝐷, тогда 𝑆𝐴𝐵𝐷 = 𝐴𝐷 ∙ 𝐵𝐻. 2 1 Пусть 𝐷𝐻1 – высота, а 𝐵𝐶 – основание ∆𝐵𝐶𝐷, тогда 𝑆𝐵𝐶𝐷 = 𝐵𝐶 ∙ 𝐷𝐻1 . 2 Так как 𝐵𝐻 и 𝐷𝐻1 высоты оной трапеции, то 𝐵𝐻 = 𝐷𝐻1 . 1 1 1 1 1 Значит, 𝑆𝐴𝐵𝐶𝐷 = 𝐴𝐷 ∙ 𝐵𝐻 + 𝐵𝐶 ∙ 𝐷𝐻1 = 𝐴𝐷 ∙ 𝐵𝐻 + 𝐵𝐶 ∙ 𝐵𝐻 = 𝐵𝐻(𝐴𝐷 + 𝐵𝐶) = 𝐴𝐷+𝐵𝐶 2 2 2 2 2 = ∙ 𝐵𝐻. 2 3. Подобны ли треугольники 𝐴𝐵𝐶 и 𝐴1 𝐵1 𝐶1 , если 𝐴𝐵 = 3 см, 𝐵𝐶 = 5 см, 𝐴𝐶 = 7 см, 𝐴1 𝐵1 = 4,5 см, 𝐵1 𝐶1 = 7,5 см, 𝐴1 𝐶1 = 10,5 см? Билет 7 1. Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Синус острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. 𝐵𝐶 𝐴𝐵 𝐴𝐶 cos 𝛼 = 𝐴𝐵 𝐵𝐶 𝑡𝑔 𝛼 = 𝐴𝐶 sin 𝛼 = Тангенс угла равен отношению синуса к косинусу этого угла (𝑡𝑔 𝛽 = sin 𝛽 cos 𝛽 ). Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны. Основное тригонометрическое тождество: sin2 𝑥 + cos 2 𝑥 = 1. 2. Признаки равенства треугольников (формулировка, доказательство одного из признаков). I признак. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Дано: ∆𝐴𝐵𝐶 и ∆𝐴1 𝐵1 𝐶1 𝐴𝐶 = 𝐴1 𝐶1 , 𝐴𝐵 = 𝐴1 𝐵1 , ∠𝐴 = ∠𝐴1 Доказать: ∆𝐴𝐵𝐶 = ∆𝐴1 𝐵1 𝐶1 Доказательство: Так как ∠𝐴 = ∠𝐴1 , то треугольник 𝐴𝐵𝐶 можно наложить на треугольник 𝐴1 𝐵1 𝐶1 , так что вершина 𝐴 совместится с вершиной 𝐴1 , а стороны 𝐴𝐵 и 𝐴𝐶 наложатся соответственно на лучи 𝐴1 𝐵1 и 𝐴1 𝐶1 . Поскольку 𝐴𝐵 = 𝐴1 𝐵1 , 𝐴𝐶 = 𝐴1 𝐶1 , то сторона 𝐴𝐵 совместится со стороной 𝐴1 𝐵1 , а сторона 𝐴𝐶 – со стороной 𝐴1 𝐶1 ; в частности, совместятся точки 𝐵 и 𝐵1 , 𝐶 и 𝐶1 . Следовательно, совместятся стороны 𝐵𝐶 и 𝐵1 𝐶1 . Итак, треугольники 𝐴𝐵𝐶 и 𝐴1 𝐵1 𝐶1 полностью совместятся, значит они равны. II признак. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Дано: ∆𝐴𝐵𝐶 и ∆𝐴1 𝐵1 𝐶1 𝐴𝐵 = 𝐴1 𝐵1 , ∠𝐴 = ∠𝐴1 , ∠𝐵 = ∠𝐵1 Доказать: ∆𝐴𝐵𝐶 = ∆𝐴1 𝐵1 𝐶1 Доказательство: Наложим треугольник 𝐴𝐵𝐶 на треугольник 𝐴1 𝐵1 𝐶1 так, чтобы вершина 𝐴 совместилась с вершиной 𝐴1 , сторона 𝐴𝐵 – с равной ей стороной 𝐴1 𝐵1 , и вершины 𝐶 и 𝐶1 оказались по одну сторону от прямой 𝐴1 𝐵1 . Так как ∠𝐴 = ∠𝐴1 и ∠𝐵 = ∠𝐵1 , то сторона 𝐴𝐶 наложится на луч 𝐴1 𝐶1 , а сторона 𝐵𝐶 – на луч 𝐵1 𝐶1 . Поэтому вершина 𝐶 – общая точка сторон 𝐴𝐶 и 𝐵𝐶- окажется лежащей на луче 𝐴1 𝐶1 , так и на луче 𝐵1 𝐶1 и, следовательно, совместится с общей точкой этих лучей – вершиной 𝐶1 . Значит, совместятся стороны 𝐴𝐶 и 𝐴1 𝐵1 , 𝐵𝐶 и 𝐵1 𝐶1 . Итак, треугольники 𝐴𝐵𝐶 и 𝐴1 𝐵1 𝐶1 полностью совместятся, значит они равны. III признак. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Дано: ∆𝐴𝐵𝐶 и ∆𝐴1 𝐵1 𝐶1 𝐴𝐵 = 𝐴1 𝐵1 , 𝐴𝐶 = 𝐴1 𝐶1 , 𝐵𝐶 = 𝐵1 𝐶1 Доказать: ∆𝐴𝐵𝐶 = ∆𝐴1 𝐵1 𝐶1 Доказательство: Приложим треугольник 𝐴𝐵𝐶 к треугольнику 𝐴1 𝐵1 𝐶1 так, чтобы вершина 𝐴 совместилась с вершиной 𝐴1 , вершина 𝐵 – с вершиной 𝐵1 , а вершины 𝐶 и 𝐶1 оказались по разные стороны от прямой 𝐴1 𝐵1 . Возможны три случая: 1) Луч 𝐶𝐶1 проходит внутри угла 𝐴1 𝐶1 𝐵1 (рис.а); 2) Луч 𝐶𝐶1 совпадает с одной из сторон этого угла (рис.б); 3) Луч 𝐶𝐶1 проходит вне угла 𝐴1 𝐶1 𝐵1 (рис.в). Рассмотрим 1 случай (остальные самостоятельно): Так как 𝐴𝐶 = 𝐴1 𝐶1 и 𝐵𝐶 = 𝐵1 𝐶1 , то ∆𝐴1 𝐶1 𝐶 и ∆𝐵1 𝐶1 𝐶 – равнобедренные. По теореме о свойстве углов равнобедренного треугольника ∠1 = 2∠, ∠3 = ∠4, поэтому ∠𝐴1 𝐶𝐵1 = ∠𝐴1 𝐶1 𝐵1 . Итак, 𝐴𝐶 = 𝐴1 𝐶1 , 𝐵𝐶 = 𝐵1 𝐶1 , ∠𝐶 = ∠𝐶1 . Следовательно, треугольники 𝐴𝐵𝐶 и 𝐴1 𝐵1 𝐶1 равны по первому признаку равенства треугольников. 3. Найдите площадь равнобедренного треугольника, если его основание равно 10 см, а боковая сторона равна 13 см. Билет 8 1. Определение окружности и ее элементы. Окружность – геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности. Радиус – Отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одинаковую длину. Отрезок, соединяющий две любые точки окружности – хорда. Хорда, проходящая через центр окружности, называется диаметром. Диаметр в два раза больше радиуса: 𝑑 = 2𝑟. Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой. Часть плоскости, ограниченная окружностью, называется кругом. 2. Теорема о средней линии треугольника (формулировка, доказательство). Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника. Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Дано: ∆𝐴𝐵𝐶 𝑀𝑁- средняя линия. Доказать: 1) 𝑀𝑁 ∥ 𝐴𝐶 1 2) 𝑀𝑁 = 𝐴𝐶 2 Доказательство: 1) ∆𝐴𝐵𝐶~∆𝑀𝑁𝐵 – по второму признаку (∠𝐵 – общий, 𝑀𝑁 1 𝐵𝑀 𝐵𝐴 = 𝐵𝑁 𝐵𝐶 1 = ), поэтому ∠1 = ∠2 и 2 = . 2 Т.к. ∠1 и ∠2 – соответственные при 𝑀𝑁 и 𝐴𝐶и ∠1 = ∠2, то 𝑀𝑁 ∥ 𝐴𝐶. 𝑀𝑁 1 1 2) Т.к. = , то 𝑀𝑁 = 𝐴𝐶. 𝐴𝐶 𝐴𝐶 2 2 3. У подобных треугольников сходственные стороны равны 7 см и 35 см. Площадь одного треугольника равна 27 см². Найдите площадь другого треугольника. Билет 9 1. Определение четырехугольника. Сумма углов четырех угольника. Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Две несмежные стороны четырехугольника называются противоположными сторонами. Две вершины, не являющиеся соседними, называются противоположными вершинами. Четырехугольник имеет две диагонали. Сумма длин четырёх сторон четырехугольника называется его периметром. Сумма углов выпуклого четырехугольника равна 𝟑𝟔𝟎°. 2. Теорема о вписанном угле (формулировка, доказательство). Теорема: Вписанный угол измеряется половиной дуги на которую он опирается. Дано: ∠𝐴𝐵𝐶 – вписанный в окружность с центром 𝑂 Доказать: 1 ∠𝐴𝐵𝐶 = ∪ 𝐴𝐶 2 Доказательство: 1) 𝐵𝑂 совпадает с одной из сторон 𝐴𝐵𝐶 (рис.а) ∠𝐴𝑂𝐶 – центральный угол. ∆𝐴𝐵𝐶 – равнобедренный с основанием 𝐴𝐵. ∠𝐴𝑂𝐶 – внешний угол для ∆𝐴𝐵𝐶, значит ∠𝐴𝑂𝐶 = ∠1 + ∠2 = 2∠1. 1 2∠1 =∪ 𝐴𝐶 или ∠𝐴𝐵𝐶 = ∠1 = ∪ 𝐴𝐶. 2 2) Луч 𝑂𝐵 делит ∠𝐴𝐵𝐶 на два угла (рис.б). 1 Луч 𝑂𝐵 пересекает ∪ 𝐴𝐶 в точке 𝐷. Значит, из доказанного в п.1) ∠𝐴𝐵𝐷 = ∪ 𝐴𝐷 и 1 ∠𝐷𝐵𝐶 = 𝐷𝐶. 2 2 1 1 1 1 ∠𝐴𝐵𝐶 = ∠𝐴𝐵𝐷 + ∠𝐷𝐵𝐶 = ∪ 𝐴𝐷 + ∪ 𝐷𝐶 = (∪ 𝐴𝐷 +∪ 𝐷𝐶) = ∪ 𝐴𝐶. 2 2 2 2 3) Луч 𝑂𝐵 не делит ∠𝐴𝐵𝐶 на два угла и не совпадает со стороной этого угла (рис.в). 1 1 ∪ 𝐴𝐶 =∪ 𝐴𝐷 −∪ 𝐶𝐷. ∠𝐴𝐵𝐷 = ∪ 𝐴𝐷 и ∠𝐶𝐵𝐷 = ∪ 𝐶𝐷 (по п.1)). 1 1 2 1 2 1 ∠𝐴𝐵𝐷 − ∠𝐶𝐵𝐷 = ∪ 𝐴𝐷 − ∪ 𝐶𝐷 = (∪ 𝐴𝐷 −∪ 𝐶𝐷) = ∪ 𝐴𝐶. 2 2 2 2 3. Найдите площадь равнобедренной трапеции, если ее основания равны 8 см и 12 см, а боковая сторона равна 10 см. Билет 10 1. Значение синуса, косинуса и тангенса для углов 30°, 45° и 60°. 𝛼 sin 𝛼 30° 45° 1 √2 2 2 cos 𝛼 √3 √2 2 2 𝑡𝑔 𝛼 1 √3 3 2. Теорема о касательной к окружности (формулировка, доказательство). 60° √3 2 1 2 √3 Теорема: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Дано: Окружность с центром в точке 𝑂. 𝑂𝐴 – радиус. 𝑝 – касательная. Доказать: 𝑂𝐴 ⊥ 𝑝. Доказательство: Предположим, что радиус 𝑂𝐴 не перпендикулярен касательной 𝑝. Тогда радиус 𝑂𝐴 является наклонной к прямой 𝑝. Т.к. перпендикуляр к прямой 𝑝 меньше наклонной, то прямая 𝑝 пересекает окружность в двух точках, а значит не является касательной, но это противоречит условию. Следовательно, 𝑂𝐴 ⊥ 𝑝. 3. Центральный угол 𝐴𝑂𝐶 равен 130°. Чему равен вписанный угол 𝐴𝐵𝐶? Билет 11 1. Треугольник и его элементы. Виды треугольников. Треугольник – это геометрическая фигура, состоящая из трех точек (вершин) не лежащих на одной прямой и попарно соединенных (сторон). Треугольник имеет три вершины, три стороны и три угла. Сумма длин трех сторон треугольника называется его периметром. Два треугольника называются равными, если при наложении они совпадают. Если два треугольника равны, то элементы(т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. В равных треугольниках против соответственно равных сторон лежат равные углы. В равных треугольниках против соответственно равных углов лежат равные стороны. Виды треугольников: По сторонам: o Разносторонний (все стороны не равны) o Равнобедренный (две стороны равны, а третья нет) o Равносторонний (все стороны равны) По углам: o Остроугольный (все углы острые) o Тупоугольный (один угол тупой, остальные острые) o Прямоугольный (один угол равен 90° остальные острые) 2. Теорема о произведении отрезков пересекающихся хорд (формулировка, доказательство). Теорема: Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Дано: Окружность. 𝐴𝐵 и 𝐶𝐷 – хорды. 𝐸 точка пересечения хорд Доказать: 𝐴𝐸 ∙ 𝐸𝐵 = 𝐶𝐸 ∙ 𝐸𝐷 Доказательство: ∆𝐴𝐷𝐸~∆𝐶𝐵𝐸 по двум углам (∠3 = ∠4 – вертикальные, ∠1 = ∠2 – опираются на одну 𝐴𝐸 𝐷𝐸 дугу 𝐷𝐵). Значит, = ⇒ 𝐴𝐸 ∙ 𝐸𝐵 = 𝐶𝐸 ∙ 𝐸𝐷. 𝐶𝐸 𝐵𝐸 3. Один из смежных углов на 40° больше другого. Найдите эти углы. Билет 12 1. Ромб и квадрат. Свойства ромба и квадрата. Ромб – параллелограмм, у которого все стороны равны. Квадрат – прямоугольник, у которого все стороны равны. Свойства ромба: Противоположные стороны и углы равны. Диагонали пересекаются и точкой пересечения делятся пополам. Диагонали ромба взаимно перпендикулярны. Диагонали ромба делят его углы пополам. Свойства квадрата Противоположные стороны и углы равны. Диагонали пересекаются и точкой пересечения делятся пополам. Диагонали квадрата взаимно перпендикулярны. Диагонали квадрата делят его углы пополам. Все углы квадрата прямые. Диагонали квадрата равны. 2. Теорема об отношении площадей треугольников, имеющих равные углы. Теорема: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы. Дано: ∆𝐴𝐵𝐶 и ∆𝐴1 𝐵1 𝐶1 ∠𝐴 = ∠𝐴1 𝑆 площадь ∆𝐴𝐵𝐶 𝑆1 площадь ∆𝐴1 𝐵1 𝐶1 Доказать: 𝑆 𝐴𝐵∙𝐴𝐶 = 𝑆1 𝐴1 𝐵1 ∙𝐴1 𝐶1 Доказательство: Наложим 𝐴1 𝐵1 𝐶1 на 𝐴𝐵𝐶 так, чтобы вершина 𝐴1 совместилась с вершиной 𝐴, а стороны 𝐴1 𝐵1 и 𝐴1 𝐶1 соответственно наложились на лучи 𝐴𝐵 и 𝐴𝐶. 𝑆 𝐴𝐵 ∆𝐴𝐵𝐶 и ∆𝐴𝐵1 𝐶 имеют общую высоту 𝐶𝐻, поэтому = . 𝑆𝐴𝐵1𝐶 𝐴𝐵1 𝑆𝐴𝐵1 𝐶 ∆𝐴𝐵1 𝐶 и ∆𝐴𝐵1 𝐶1 также имеют общую высоту 𝐵1 𝐻1 , поэтому 𝑆 𝑆𝐴𝐵1𝐶 или 𝑆 = 𝑆1 ∙ 𝑆𝐴𝐵1 𝐶 𝑆𝐴𝐵1 𝐶1 = 𝐴𝐵∙𝐴𝐶 𝐴1 𝐵1 ∙𝐴1 𝐶1 𝑆 𝑆𝐴𝐵1 𝐶1 = 𝐴𝐵 𝐴𝐵1 ∙ 𝐴𝐶 𝐴𝐶1 𝑆𝐴𝐵1 𝐶1 = 𝐴𝐶 𝐴𝐶1 . 3. Площадь прямоугольника равна 75 см². Найдите стороны этого прямоугольника, если одна из них в 3 раза больше другой. Билет 13 1. Трапеция. Виды трапеции. Трапеция – четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны – основания. Не параллельные стороны боковые стороны. Виды трапеций: Равнобедренная трапеция – трапеция, у которой боковые стороны равны. Прямоугольная трапеция – трапеция, у которой один из углов прямой. Свойства равнобедренной трапеции: Углы при основании равны. Диагонали равны. 2. Признаки параллельности прямых (формулировка, доказательство). Теорема: Если пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Дано: 𝑎 и 𝑏 – прямые 𝐴𝐵 – секущая ∠1 = ∠2 Доказать: 𝑎∥𝑏 Доказательство: 1) Если ∠1 = ∠2 = 90°, то 𝑎 ⊥ 𝐴𝐵 и 𝑏 ⊥ 𝐴𝐵 , следовательно 𝑎 ∥ 𝑏. 2) Если ∠1 и ∠2 не прямые. Из середины 𝑂 отрезка 𝐴𝐵 проведем перпендикуляр 𝑂𝐻 к прямой 𝑎. На прямой 𝑏 от точки 𝐵 отложим отрезок 𝐵𝐻1 , равный отрезку 𝐴𝐻 и проведем отрезок 𝑂𝐻1 . ∆𝑂𝐴𝐻 = ∆𝑂𝐻1 𝐵по двум сторонам и углу между ними (𝐴𝑂 = 𝑂𝐵, 𝐴𝐻 = 𝐵𝐻1 , ∠1 = ∠2), поэтому ∠3 = ∠4 и ∠5 = ∠6. Т.к. ∠3 = ∠4, то точка 𝐻1 лежит на продолжении луча 𝑂𝐻, т.е. точки 𝐻, 𝑂 и 𝐻1 лежат на одной прямой, а т.к. ∠5 = ∠6 = 90°, то 𝑎 ⊥ 𝐻𝐻1 и 𝑏 ⊥ 𝐻𝐻1 , значит 𝑎 ∥ 𝑏. Теорема: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Дано: 𝑎и𝑏 𝑐 – секущая ∠1 = ∠2 Доказать: 𝑎∥𝑏 Доказательство: ∠2 = ∠3 – вертикальные и ∠2 = ∠1 – по условию, значит ∠1 = ∠3 – накрест лежащие, а следовательно 𝑎 ∥ 𝑏 (по первому признаку). Теорема: Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны. Дано: 𝑎и𝑏 𝑐 – секущая ∠1 + ∠4 = 180° Доказать: 𝑎∥𝑏 Доказательство: ∠3 и ∠4 – смежные, значит ∠3 + ∠4 = 180°, следовательно, ∠3 = 180° − ∠4. ∠1 + ∠4 = 180° – по условию, а значит ∠1 = 180° − ∠4. Значит, ∠1 = ∠3 – накрест лежащие, а следовательно 𝑎 ∥ 𝑏 (по первому признаку). 3. Найдите площадь равностороннего треугольника, сторона которого равна 12 см. Билет 14 1. Дуга окружности. Вписанный угол. Центральный угол. Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой. Полуокружность – дуга, концы которой соединяются диаметром. Центральный угол – угол с вершиной в центре окружности. Центральный угол равен дуге, на которую он опирается. ∠𝐴𝑂𝐵 =∪ 𝐴𝐿𝐵 Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность. Вписанный угол равен половине дуги , на которую он опирается. 1 ∠𝐴𝐵𝐶 = ∪ 𝐴𝑀𝐶 2 2. Признаки подобия треугольников (формулировка, доказательство одно признака). Теорема: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. Дано: ∆𝐴𝐵𝐶 и ∆𝐴1 𝐵1 𝐶1 ∠𝐴 = ∠𝐴1 и ∠𝐵 = ∠𝐵1 Доказать: ∆𝐴𝐵𝐶~∆𝐴1 𝐵1 𝐶1 Доказательство: По теореме о сумме углов треугольника: ∠𝐶 = 180° − (∠𝐴 + ∠𝐵) и ∠𝐶1 = 180° − (∠𝐴1 + ∠𝐵1 ), т.к. ∠𝐴 = ∠𝐴1 и ∠𝐵 = ∠𝐵1 , то ∠𝐶 = ∠𝐶1 . 𝑆 𝐴𝐵∙𝐴𝐶 𝑆 𝐶𝐵∙𝐴𝐶 Так как ∠𝐴 = ∠𝐴1 и ∠𝐶 = ∠𝐶1 , то 𝐴𝐵𝐶 = и 𝐴𝐵𝐶 = , следовательно 𝐴𝐵 𝐴1 𝐵1 = 𝐵𝐶 𝐵1 𝐶1 𝑆𝐴1𝐵1𝐶1 . 𝐴1 𝐵1 ∙𝐴1 𝐶1 𝑆𝐴1 𝐵1𝐶1 𝐶1 𝐵1 ∙𝐴1 𝐶1 Аналогично, если ∠𝐴 = ∠𝐴1 и ∠𝐵 = ∠𝐵1 , то 𝐵𝐶 𝐵1 𝐶1 = 𝐴𝐶 𝐴1 𝐶1 . Значит, т.к. все углы треугольников равны, а сходственные стороны пропорциональны, то ∆𝐴𝐵𝐶~∆𝐴1 𝐵1 𝐶1 по определению. Терема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Дано: ∆𝐴𝐵𝐶 и ∆𝐴1 𝐵1 𝐶1 𝐴𝐵 ∠𝐴 = ∠𝐴1 и = 𝐴1 𝐵1 𝐴𝐶 𝐴1 𝐶1 Доказать: ∆𝐴𝐵𝐶~∆𝐴1 𝐵1 𝐶1 Доказательство: Рассмотрим ∆𝐴𝐵𝐶2 , у которого ∠1 = ∠𝐴1 , ∠2 = ∠𝐵1 . 𝐴𝐵 ∆𝐴𝐵𝐶2 ~∆𝐴1 𝐵1 𝐶1 по двум углам, следовательно = 𝐴1 𝐵1 𝐴𝐶 𝐴1 𝐶1 и т.к. 𝐴𝐵 𝐴1 𝐵1 = 𝐴𝐶 𝐴1 𝐶1 по условию, то 𝐴𝐶 = 𝐴𝐶2 . ∆𝐴𝐵𝐶 = ∆𝐴𝐵𝐶2 по двум сторонам и углу между ними (𝐴𝐵 – общая, 𝐴𝐶 = 𝐴𝐶2 и ∠𝐴 = ∠1, поскольку ∠𝐴 = ∠𝐴1 = ∠1). Следовательно, ∠𝐵 = ∠2 = ∠𝐵1 . Значит, т.к. ∠𝐴 = ∠𝐴1 – по условию и ∠𝐵 = ∠𝐵1 , то ∆𝐴𝐵𝐶~∆𝐴1 𝐵1 𝐶1 по первому признаку подобия треугольников. Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Дано: ∆𝐴𝐵𝐶 и ∆𝐴1 𝐵1 𝐶1 𝐴𝐵 𝐵𝐶 𝐴𝐶 = = 𝐴1 𝐵1 𝐵1 𝐶1 𝐴1 𝐶1 Доказать: ∆𝐴𝐵𝐶~∆𝐴1 𝐵1 𝐶1 Доказательство: Рассмотрим ∆𝐴𝐵𝐶2 , у которого ∠1 = ∠𝐴1 , ∠2 = ∠𝐵1 . 𝐴𝐵 ∆𝐴𝐵𝐶2 ~∆𝐴1 𝐵1 𝐶1 по двум углам, следовательно = 𝐴𝐶 𝐴1 𝐶1 𝐴1 𝐵1 𝐵𝐶2 𝐵1 𝐶1 = 𝐶2 𝐴 𝐶1 𝐴1 и т.к. 𝐴𝐵 𝐴1 𝐵1 = 𝐵𝐶 𝐵1 𝐶1 = по условию, то 𝐴𝐶 = 𝐴𝐶2 , 𝐵𝐶 = 𝐵𝐶2 . ∆𝐴𝐵𝐶 = ∆𝐴𝐵𝐶2 по трем сторонам (𝐴𝐵 – общая, 𝐴𝐶 = 𝐴𝐶2 и 𝐵𝐶 = 𝐵𝐶2 ). Следовательно, ∠𝐴 = ∠1 = ∠𝐴1 . Значит, т.к. 𝐴𝐵 𝐴1 𝐵1 = 𝐴𝐶 𝐴1 𝐶1 – по условию и ∠𝐴 = ∠𝐴1 , то ∆𝐴𝐵𝐶~∆𝐴1 𝐵1 𝐶1 по второму признаку подобия треугольников. 3. Найдите площадь прямоугольника, если одна из его сторон равна 5 см, а угол между диагоналями равен 60°. Билет 15 1. Равнобедренный треугольник. Равнобедренный треугольник – это треугольник, у которого две стороны равны. Равные стороны называются боковыми сторонами. Третья, не равная сторона – основание. Равносторонний треугольник – треугольник, у которого все стороны равны. Свойства равнобедренного треугольника: Углы при основании равны. Биссектриса, проведенная к основанию, является медианой и высотой. 2. Теорема о серединном перпендикуляре к отрезку (формулировка, доказательство). Серединный перпендикуляр к отрезку – это прямая, проходящая через середину данного отрезка и перпендикулярная к нему. Теорема: Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно, каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре. Дано: 1) 𝐴𝐵 отрезок 𝑚 – серединный перпендикуляр 𝑂 – середина отрезка 2) 𝐵 отрезок 𝑚 – серединный перпендикуляр 𝑂 – середина отрезка 𝐴𝑁 = 𝑁𝐵 Доказать: 1) 𝐴𝑀 = 𝐵𝑀 (рис.а) 2) 𝑁 ∈ 𝑚 (рис.б) Доказательство: 1) Если точка 𝑀 совпадает с точкой 𝑂, то 𝐴𝑀 = 𝑀𝐵, так как 𝑂 середина 𝐴𝐵. Если 𝑀 и 𝑂 различные точки: ∆𝑂𝐴𝑀 и ∆𝑂𝑀𝐵 – прямоугольные, ∆𝑂𝐴𝑀 = ∆𝑂𝑀𝐵 по двум катетам (𝑂𝐴 = 𝑂𝐵, 𝑂𝑀 – общий катет), следовательно, 𝐴𝑀 = 𝐵𝑀. 2) Если 𝑁 ∈ 𝐴𝐵, то она совпадает с серединой 𝑂 отрезка 𝐴𝐵, следовательно 𝑁 ∈ 𝑚. Если 𝑁 ∉ 𝐴𝐵, то ∆𝐴𝑁𝐵 – равнобедренный, т.к. 𝐴𝑁 = 𝐵𝑁. 𝑁𝑂 – медиана, а значит и высота. Таким образом, 𝑁𝑂 ⊥ 𝐴𝐵, поэтому прямые 𝑂𝑁 и 𝑚 совпадают, т.е. 𝑁 ∈ 𝑚. 3. В прямоугольном треугольнике с острым углом 45° гипотенуза равна 32 см. Найдите площадь этого треугольника. Билет 16 1. Определение подобных треугольников. Стороны, лежащие напротив соответственно равных углов двух треугольников, называются сходственными. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. Отношение сходственных сторон, называется коэффициентом подобия треугольников (𝑘). ∆𝐴𝐵𝐶~∆𝐴1 𝐵1 𝐶1 , если ∠𝐴 = ∠𝐴1 , ∠𝐵 = ∠𝐵1 , 𝐴𝐵 𝐵𝐶 𝐴𝐶 ∠𝐶 = ∠𝐶1 и = = . 𝐴1 𝐵1 𝐴𝐵 𝐴1 𝐵1 = 𝐵𝐶 𝐵1 𝐶1 = 𝐴𝐶 𝐴1 𝐶1 𝐵1 𝐶1 𝐴1 𝐶1 =𝑘 2. Площадь прямоугольника (формулировка, доказательство). Теорема: площадь прямоугольника равна произведению его смежных сторон (𝑆 = 𝑎𝑏). Дано: Прямоугольник со сторонами 𝑎 и 𝑏 𝑆 площадь прямоугольника Доказать: 𝑆 = 𝑎𝑏. Доказательство: Достроим прямоугольник до квадрата со стороной (𝑎 + 𝑏). Площадь этого квадрата равна (𝑎 + 𝑏)2 . С другой стороны, этот квадрат состоит из Квадрата со стороной 𝑎 и площадью 𝑎2 . Квадрата со стороной 𝑏 и площадью 𝑏 2 . Двух прямоугольников с площадью 𝑆. Значит, (𝑎 + 𝑏)2 = 𝑎2 + 𝑏 2 + 2𝑆. 𝑎2 + 2𝑎𝑏 + 𝑏 2 = 𝑎2 + 𝑏 2 + 2𝑆. Следовательно, 2𝑆 = 2𝑎𝑏 ⇒ 𝑆 = 𝑎𝑏. 3. Сумма трех углов параллелограмма равна 254°. Найдите углы параллелограмма. Билет 17 1. Взаимное расположение окружности и прямой. Определение касательной к окружности. Пусть 𝑟 – радиус окружности, 𝑑 – расстояние от центра окружности до прямой. Если 𝑑 < 𝑟. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки. Если 𝑑 = 𝑟. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну обую точку. Если 𝑑 > 𝑟. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек. Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. 2. Признаки параллелограмма (формулировка, доказательство одного признака). Теорема: Если в четырёхугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм. Дано: 𝐴𝐵𝐶𝐷 – четырехугольник 𝐴𝐵 = 𝐶𝐷 𝐴𝐵 ∥ 𝐶𝐷 Доказать: 𝐴𝐵𝐶𝐷 - параллелограмм Доказательство: Проведем диагональ 𝐴𝐶.∆𝐴𝐵𝐶 = ∆𝐴𝐶𝐷 по двум сторонам и углу между ними ( 𝐴𝐶 – общая сторона, 𝐴𝐵 = 𝐶𝐷 по условию, ∠1 = ∠2 накрест лежащие при 𝐴𝐵 ∥ 𝐶𝐷 и секущей 𝐴𝐶) поэтому ∠3 = ∠4 и они накрест лежащие при 𝐴𝐷 и 𝐵𝐶и секущей 𝐴𝐶, следовательно 𝐴𝐷 ∥ 𝐶𝐵. Таким образом, т.к. 𝐴𝐵 ∥ 𝐶𝐷 – по условию, 𝐴𝐷 ∥ 𝐶𝐵, значит 𝐴𝐵𝐶𝐷 – параллелограмм по определению. Теорема: Если в четырёхугольнике противолежащие стороны попарно равны, то этот четырёхугольник параллелограмм. Дано: 𝐴𝐵𝐶𝐷 – четырехугольник 𝐴𝐵 = 𝐶𝐷 𝐶𝐵 = 𝐴𝐷 Доказать: 𝐴𝐵𝐶𝐷 - параллелограмм Доказательство: Проведем диагональ 𝐴𝐶.∆𝐴𝐵𝐶 = ∆𝐴𝐶𝐷 по трем сторонам ( 𝐴𝐶 – общая сторона, 𝐴𝐵 = 𝐶𝐷 по условию, 𝐶𝐵 = 𝐴𝐷 по условию) поэтому ∠1 = ∠2 и они накрест лежащие при 𝐴𝐵 и 𝐷𝐶 и секущей 𝐴𝐶, следовательно 𝐴𝐵 ∥ 𝐶𝐷. Таким образом, т.к. 𝐴𝐵 = 𝐶𝐷 – по условию, 𝐴𝐵 ∥ 𝐶𝐷, значит 𝐴𝐵𝐶𝐷 – параллелограмм по 1 признаку параллелограмма. Теорема: Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. Дано: 𝐴𝐵𝐶𝐷 – четырехугольник 𝐴𝑂 = 𝑂𝐶 𝐷𝑂 = 𝑂𝐵 Доказать: 𝐴𝐵𝐶𝐷 - параллелограмм Доказательство: ∆𝐴𝑂𝐵 = ∆𝐶𝑂𝐷 по двум сторонам и углу между ними (𝐴𝑂 = 𝑂𝐶, 𝐵𝑂 = 𝑂𝐷 по условию, ∠𝐴𝑂𝐵 = ∠𝐶𝑂𝐷 – вертикальные), поэтому 𝐴𝐵 = 𝐶𝐷 и ∠1 = ∠2 и они накрест лежащие при 𝐴𝐵 и 𝐷𝐶 и секущей 𝐴𝐶, следовательно 𝐴𝐵 ∥ 𝐶𝐷. Таким образом, т.к. 𝐴𝐵 = 𝐶𝐷 – по условию, 𝐴𝐵 ∥ 𝐶𝐷, значит 𝐴𝐵𝐶𝐷 – параллелограмм по 1 признаку параллелограмма. 3. Подобны ли треугольники 𝐴𝐵𝐶 и 𝐴1 𝐵1 𝐶1 , если 𝐴𝐵 = 10 см, 𝐵𝐶 = 8 см, 𝐴𝐶 = 7 см, 𝐴1 𝐵1 = 30 см, 𝐵1 𝐶1 = 21 см, 𝐴1 𝐶1 = 24 см? Билет 18 1. Описанная окружность. Свойства. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность. Теорема: Около любого треугольника можно описать окружность. Замечания: Около треугольника можно описать только одну окружность. Около четырехугольника не всегда можно описать окружность. Свойство: В любом вписанном четырехугольнике сумма противоположных углов равна 180°. Обратно, если сумма противолежащих углов четырехугольника равна 180°, то около него можно описать окружность. 2. Теорема об отношении площадей подобных треугольников (формулировка, доказательство). Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Дано: ∆𝐴𝐵𝐶~∆𝐴1 𝐵1 𝐶1 𝑘 – коэффициент подобия. 𝑆 – площадь ∆𝐴𝐵𝐶 𝑆1 – площадь ∆𝐴1 𝐵1 𝐶1 Доказать: 𝑆 = 𝑘2 𝑆1 Так как ∠𝐴 = ∠𝐴1 , то 𝑆 𝑆1 = 𝐴𝐵∙𝐴𝐶 𝐴1 𝐵1 ∙𝐴1 𝐶1 Доказательство: (по теореме об отношении площадей треугольников, имеющих по равному углу). 𝐴𝐵 𝐵𝐶 𝐴𝐶 𝐴𝐵 𝐴𝐶 Из равенства = = = 𝑘 имеем =𝑘и = 𝑘, поэтому 𝐴1 𝐵1 𝐵1 𝐶1 𝐴1 𝐶1 𝐴1 𝐵1 𝐴1 𝐶1 𝑆 𝐴𝐵 ∙ 𝐴𝐶 = = 𝑘 ∙ 𝑘 = 𝑘2. 𝑆1 𝐴1 𝐵1 ∙ 𝐴1 𝐶1 3. Периметр квадрата равен 32 см. Найдите площадь этого квадрата. Билет 19 1. Многоугольник. Выпуклый многоугольник. Диагональ многоугольника. Периметр многоугольника. Многоугольник – замкнутая ломаная звенья, которой не пересекаются. Сторона многоугольника – звенья ломаной. Вершины многоугольника – вершины ломаной. Сумма длин всех сторон многоугольника – периметр многоугольника. Многоугольник с 𝑛 вершинами называется -угольником. Две вершины многоугольника называются соседними, если они принадлежат одной стороне. Отрезок, соединяющий две не соседние вершины, называется диагональю многоугольника. Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Сумма углов выпуклого -угольника равна (𝑛 − 2) ∙ 180°. Внешним углов выпуклого многоугольника называется угол, смежный с углом многоугольника. Сумма внешних углов выпуклого многоугольника равна 360°. 2. Теорема о пересечении высот треугольника (формулировка, доказательство). Теорема: Высоты треугольника (или их продолжения) пересекаются в одной точке. Дано: ∆𝐴𝐵𝐶 𝐴𝐴1 , 𝐵𝐵1 , 𝐶𝐶1 - высоты Доказать: 𝐴𝐴1 , 𝐵𝐵1 и 𝐶𝐶1 пересекаются в одной точке. Доказательство: Проведем через каждую вершину треугольника 𝐴𝐵𝐶 прямую, параллельную противоположной стороне. Получим ∆𝐴2 𝐵2 𝐶2 . Точки 𝐴, 𝐵 и 𝐶 – середины сторон ∆𝐴2 𝐵2 𝐶2 . Действительно, 𝐴𝐵 = 𝐴2 𝐶 и 𝐴𝐵 = 𝐶𝐵2 как противолежащие стороны параллелограммов 𝐴𝐵𝐴2 𝐶 и 𝐴𝐵𝐶𝐵2 , поэтому 𝐴2 𝐶 = 𝐶𝐵2 . Аналогично 𝐶2 𝐴 = 𝐴𝐵2 и 𝐶2 𝐵 = 𝐵𝐴2 . Кроме того, как следует из построения, 𝐶𝐶1 ⊥ 𝐴2 𝐵2 , 𝐴𝐴1 ⊥ 𝐵2 𝐶2 и 𝐵𝐵1 ⊥ 𝐴2 𝐶2 . Таким образом, прямые 𝐴𝐴1 , 𝐵𝐵1 и 𝐶𝐶1 являются серединными перпендикулярами к сторонам треугольника 𝐴2 𝐵2 𝐶2 . Следовательно, они пересекаются в одной точке. 3. Вычислите сторону квадрата, если его площадь равна 144 см². Билет 20 1. Параллелограмм. Свойства параллелограмма. Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны. Свойства: В параллелограмма противолежащие стороны равны. В параллелограмме противолежащие углы равны. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. 2. Теорема о сумме углов треугольника (формулировка, доказательство). Теорема: Сумма углов треугольника равна 180°. Дано: ∆𝐴𝐵𝐶 Доказать: ∠𝐴 + ∠𝐵 + ∠𝐶 = 180° Доказательство: Пусть ∠𝐴 = ∠1, ∠𝐵 = ∠2 и ∠𝐶 = ∠3. Проведем прямую 𝑎 параллельную 𝐴𝐶. ∠1 и ∠4 накрест лежащие при 𝐴𝐶 ∥ 𝑎 и секущей 𝐴𝐵. ∠5 и ∠3 накрест лежащие при 𝐴𝐶 ∥ 𝑎 и секущей 𝐵𝐶. Значит, ∠1 = ∠4 и ∠5 = ∠3. ∠4 + ∠2 + ∠5 = 180° так как образуют развернутый угол. Таким образом, так как ∠1 = ∠4 и ∠5 = ∠3, то ∠1 + ∠2 + ∠3 = ∠𝐴 + ∠𝐵 + ∠𝐶 = 180°. 3. Периметр равнобедренного треугольника равен 45 см, а одна из его сторон больше другой на 12 см. Найдите стороны треугольника.









