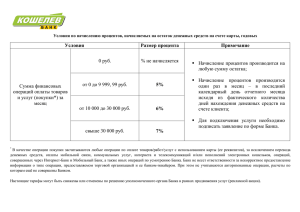
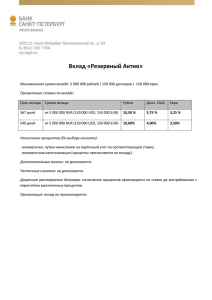
финансовая математика презентация

ФИНАНСОВАЯ МАТЕМАТИКА
1
Вопрос 1.
Основные понятия и операции
финансовой математики
2
Временная ценность денег
Помни, что деньги по природе своей плодоносны и
способны порождать новые деньги. Деньги могут
родить деньги, их отпрыски могут породить еще
больше и т.д. Тот кто изводит одну монету в пять
шиллингов, убивает все, что она могла бы произвести:
целые колонны фунтов.
М. Вебер «Протестантская этика и дух
капитализма»
3
Временная ценность денег
В рыночной экономике действует принцип
неравноценности денег, относящихся к различным
моментам времени.
Неправомерно суммировать денежные величины,
относящиеся к различным моментам времени.
4
Схема простой финансовой сделки

FV  PV  I
FV  PV  I
I
FV  PV
I
FV  PV
it 
100% 
100% d t 
100% 
100%
PV
PV
FV
FV 5
Общая структура ставки
it  i  f  E p  g (t )
где i норма процента (компенсация кредитору за отказ
использовать в других целях предоставляемую сумму в
течение времени;
f - фактор риска ( за неопределённость в получении
процентов или всей суммы по истечение срока кредита);
Ep
инфляционная
добавка
(за
уменьшение
покупательной способности денег за время );
g(t) - компенсация, зависящая от срока , при этом чем
больше срок кредита, тем выше эта компенсация.
6
Проценты
- декурсивный (последующий) процент, когда его
начисление производят по процентной ставке i в
конце расчетного периода;
- антисипативный (предварительный) процент, когда
начисление производят по учетной ставке d в начале
расчётного периода.
7
Процессы наращения и
дисконтирования денежных сумм
8
Способы начисления процентов
Простые
проценты
(без
(реинвестирования) процентов):
капитализации
t
FV  PV (1  i )  PV (1  ni )
T
Сложные проценты:
n
FV  PV  (1  i )  P (1  i )
k 1
n
t
n
T
9
Сравнение начисления процентов
Сравнение процессов наращения по схеме простых
процентов со схемой сложных процентов
показывает, что на временном интервале до 1 года
наращенная сумма по схеме простых процентов
оказывается больше. Отсюда вывод: кредитор
применяет схему сложных процентов на интервалах
более 1 года, а простую – на интервалах до 1 года.
10
t/T
T - обозначение интервала времени в 1 год,
измеренного в единицах времени: год = 12 месяцев =
2 полугодия = 4 квартала = 365 (366) дней. Интервал
измеряется в одноименных единицах. Поэтому
отношение безразмерное и обычно выражает число
лет и может быть целым, дробным или десятичным
числом.
11
Спасибо за внимание!