ДИСПЕРСИОННЫЙ И ФАКТОРНЫЙ АНАЛИЗ НОМЕР ДУБЛИРУЮЩЕГО ОПЫТА ЛЕКАРСТВО 1(m)

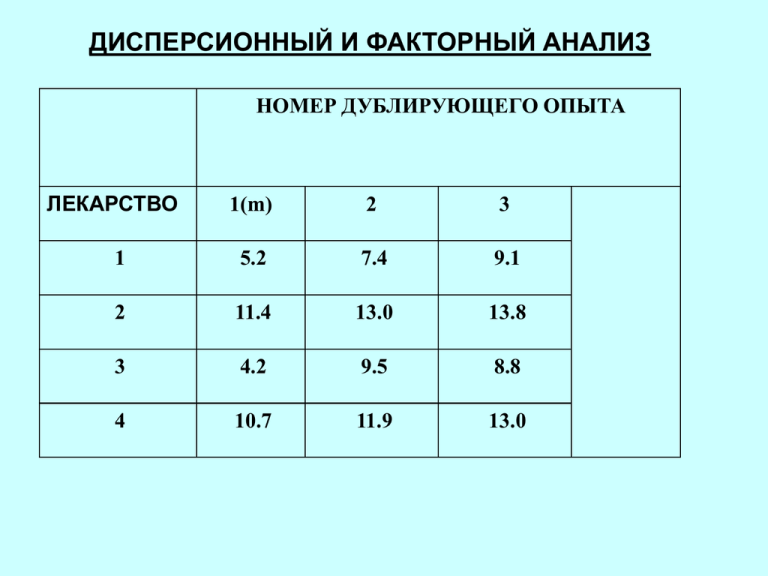
ДИСПЕРСИОННЫЙ И ФАКТОРНЫЙ АНАЛИЗ
НОМЕР ДУБЛИРУЮЩЕГО ОПЫТА
ЛЕКАРСТВО
1(m)
2
3
1
5.2
7.4
9.1
2
11.4
13.0
13.8
3
4.2
9.5
8.8
4
10.7
11.9
13.0
ДАНО:
1) Выходной параметр y может зависеть от p независимых
факторов xp, не имеющих количественного описания;
2) каждый фактор xj может варьироваться на uj уровнях;
3) полный факторный эксперимент состоит из N  u1 u2 .....ui ......un
серий независимых наблюдений;
4) каждая j к-ая серия содержит mk наблюдений y k 1, y k 2 , ..... y km
дублирующих опытов.
ТРЕБУЕТСЯ:
ОПРЕДЕЛИТЬ ВЛИЯНИЕ ФАКТОРА XJ НА ФОНЕ
СЛУЧАЙНЫХ ОШИБОК
ДОПУЩЕНИЯ:
• величина y - нормально распределённая случайная величина;
• величина y - стационарная случайная величина;
• дисперсия единичного наблюдения 2, обусловленная
случайными ошибками, постоянна во всех опытах и не зависит
x от, x. ,....., x
1
2
p
Определение. Исследование факторов по их дисперсиям
называется дисперсионным анализом.
ОДНОФАКТОРНЫЙ АНАЛИЗ
номер j
уровня
фактора Х
1
2
.
j
.
u
1 m
y j   y jl
m l 1
№ l дублирующего опыта
1
2
l
m
y11
y21
yj1
y12.
l
y1m
y22...... ..y2l...... ...y2m
yj2........ ..yjl..... ......yjm
y1
yu1
yu2...... ...yul..... . ..yum
yu
y
1 u m
1 u
y
y jl   y j .

u  m j 1 l 1
u j 1
Разложение суммы квадратов
u
m
u
m
S   ( y jl  y )  ( y jl  y j )
2
j 1 l 1
j 1 l 1
u
2
+m
( y
j 1
 yj ) =
2
j
= S0+SX
ВНУТРИ СЕРИЙ
МЕЖДУ СЕРИЙ
ОБЩАЯ ДИСПЕРСИЯ
u m
1
2
2
S2 
(
y

y
)



jl
0
um  1 j 1 l 1
1. Выборочная дисперсия рассеивания ‘внутри серий’
S0
2=
SO
u( m  1)
2. Выборочная дисперсия рассеивания между средними
серий
2
Sx
S (y )
0
j
m( u  1) m
2
x
Необходимо
S02 ЗНАЧИМО ОТЛИЧАЛОСЬ ОТ SX2
ПРОВЕРЯЕТСЯ
F расч
2
x
2
0
S

.
S
ЕСЛИ Fрасч. > F (X, 0)
влияние фактора Х
признаётся значимым
Пример.
1. Находим
3
1
1
y j   y jl  y j   y jl
3 l 1
m
y2 =12.7
y1 =7.2
y3
=7.5
y2
=11.9
1 4 3
1 u
1 4
2. Находим y 
y j l   y j   y j  9.83

4  3 j 1 l 1
u j 1
4 j 1
3. Находим сумму квадратов внутри серий
u
S0 =
m
2
(
y

y
)
 jl j
j 1 l 1
S0=[(5.2-7.2)2+(7.4-7.2)2+(9.1-7.2)2]+[(11.4-12.7)2+(13.0-12.7)2
+(13.8-12.7)2]+[(4.2-7.5)2+(9.5-7.5)2+(8.8-7.5)2]+[(10.711.9)2+(11.9-11.9)2+(13-11.9)2]=29.87.
4. Находим cумму квадратов между сериями
u
Sx=
m  ( y j  y )2
j 1
u
Sx=3
2
(
y

9
.
83
)
=3[(7.2-9.83)2+(12.7-9.83)2+(7.5 j
j 1
5. Считаем
-9.83)2+(11.9-9.83)2]=74.61.
S0
29.87
S 

 3.73
u( m  1) 4( 3  1)
2
0
Sx
74.61
S 

 8.29
m( u  1) 3(4  1)
2
x
6. Находим Fрасч=
8.29
 2.22
3.73
Ft(3,2)=19.16.
ДВУХФАКТОРНЫЙ АНАЛИЗ
№j
факто
ра Х1
№j
фактора
X2
1
1
2
y111
y112
.....
y11m1
2
…
y121
y122
.....
y12 m
yj
g
…
y1g1
y1g2
.....
y1 g m
u2
y1 u2 1
y1 u2 2
.....
y1 u2 m
y211
.....
y21m
y1
y2
.
.
j
yj11
yj12
yj1m
yj
.
u1
yg
.
yu1 11
yu1 1m
y1
....
....
yu1 u2 1
yu1 u2 m
y u1
yu 2
y
u1 m
1 m
y jg   y jgl
m l 1
1
yg 
y gjl


u1 m j 1 l 1
где
u2 m
1
yj 
y jgl


mu2 g 1 l 1
u1
u2
1
y
y jgl .


u2 u1 m j 1 g 1
S=S0+S1+S2+S12
u1 u2 m
u1 u2 m
u1
u2
j 1 g 1 l 1
j 1 g 1 l 1
j 1
g 1
S   ( y jgl  y )2   ( y jgl  y jg )2  u2 m  ( y  y )2  u1m  ( yu2  y ) 
u1 u2
 m  ( y jg  y j  y g  y )2
j 1 g 1
Оценка дисперсий
S1
S 
u1  1
S2
S 
u2  1
2
1
2
2
S12
S 
u1 u2  u1  u2  1
2
12
ЕСЛИ
2
1
2
12
2
2
2
12
S
S
F1 
 F ( 1 , 21 ), F2 
 F ( 2 , 21 )
S
S
ФАКТОРЫ Х1 И Х2 ЗНАЧИМЫ
ЕСЛИ
2
12
2
0
S
F
 F ( 12 , 0 )
S
ВЛИЯНИЕ ФАКТОРА ВЗАИМОДЕЙСТВИЯ - ЗНАЧИМО