1.Основные понятия случайной величины 1.1 Классификация случайных процессов

1.Основные понятия случайной
величины
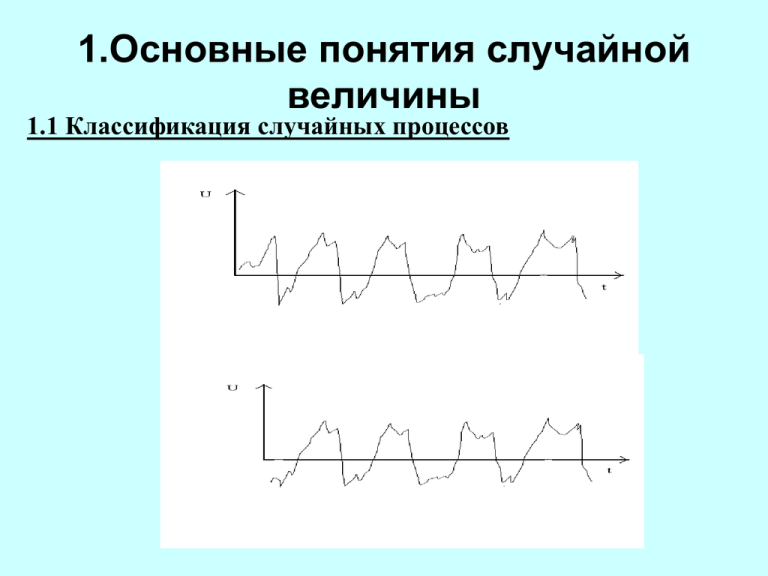
1.1 Классификация случайных процессов
Случайные
процессы
стационарные
эргодические
нестационарные
неэргодические
Классификация по
типам
нестационарности
XN(t)
t
x2(t)
t
x1(t)
t1
t1+
1 N
mx (t1 )  lim  xk (t1 )
N  N
k 1
t
- математическое
1 N
R xx (t1 , t1   )  lim  x k (t1 )  x k (t1   )
N  N
k 1
ожидание
- ковариация
Определение. Если mx(t1) и Rxx(t1, t1+) не зависят от момента
времени t1, то случайный процесс {x(t)}
называется стационарным в широком смысле
(или слабостационарным).
1.2 Эргодические случайные процессы
T
1
m x (k )  lim  x k (t )dt
T  T 0
*
T
1
Rxx (k )  lim  xk (t )  xk (t   )dt
T  T
0
Определение. Если случайный процесс {x(t)} является
стандартным, среднее и ковариация,
вычисленные по формулам (*) для различных
реализаций совпадают, то процесс называется
эргодическим.
t 1 T
1
m x ( t1 , k ) 
T
1
Rxx ( t1 , t1  T , k ) 
T
x
k
( t )dt
t1
t 1 T
x
k
( t )  xk ( t  T )dt
**
t1
Определение. Реализация называется стационарной, если
среднее и ковариация, определенные по
формулам (**) не изменяются существенно с
изменением начального момента t1.
Реализация эргодического случайного процесса
всегда стационарна.
1.3 Основные статистические характеристики
случайных процессов
1. Математическое ожидание
2. Дисперсия
3. Мода
4. Медиана
1
x
N
N
x
i 1
N
1
2 
( xi  x )

N  1 i 1
Максимальное значение плотности
вероятности
Середина выборки
5. Квартили
6. Плотность вероятности
7. Среднеквадратичное
отклонение
i

2
1.4 Графическое представление случайной величины
1) Гистограмма
Определение. Графическое изображение зависимости частоты
попадания элементов выборки от
соответствующего интервала группировки
называется гистограммой.
Цель построения -
1) Обнаружение грубых ошибок.
2) Локализация выбросов.
3) Оценка свойств распределения каждой
переменной (является ли
распределение нормальным,
вычисление среднего, дисперсии,
средний квадрат отклонения, если
нужно моментов высших порядков).
Алгоритм построения гистограммы
Имеем N измерений случайной величины
1. Определение оптимального количества интервалов группировки
k = 1+3.22 lg N, причем 5 k 30.
xmax  xmin
2. Определение длинны интервалов =
k
3. Подсчет частот fi – числа наблюдений, попавших в интервал [Ci, Ci+1),
i=1,…, k.
4. Построение частотной таблицы
Интервал группирования
Частота
[C1, C2)
[C2, C3)
…
[Ck, Ck+1)
f1
f2
5. Построение частотного графика – гистограммы
...
fk
Определение. Мода – наиболее вероятное значение
случайной величины x, соответствующее
абсолютному максимуму плотности ее
вероятности.
C i  C i 1
moda =
2
Если
fi
pi 
n
- Нормированная гистограмма
2) ПОЛИГОН ЧАСТОТ
3) ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
(интегральная форма)
k
Пусть F1  0, F2  f 1 , F3  f 1  f 2 ,..., Fk 1   f i
i 1
25% квартиль=23
Медиана=47
Процентная нормированная функция распределения проходит через
Fk 1
F1
точки
(C1 ,
n
 100%)
(C k 1 ,
n
100%)
4) Диаграмма рассеивания