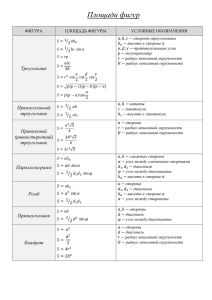
Формулы для вычисления площади правильного многоугольника
реклама

Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. МОУ СОШ № 256 г.Фокино Повторение. 1.Какая геомет рическая фигура изображена на рисунке? D 2.Какой многоугольник называет ся правильным? 3.Какая окружност ь называет ся вписанной в многоугольник? С 4.Какая окружност ь называет ся описанной около многоугольника? Е О 5.Назовит е радиус вписанной окружност А В и. Н 6.Назовит е радиус описанной окружност и. 7.Как найт и цент р вписанной в правильный многоугольник окружност и? 8.Как найт и цент р окружност и описанной около правильного многоугольника? F Проверка выполнения домашнего задания.. № 1084. β– угол, соот вет ст вующий дуге, кот орую ст ягивает ст орона многоугольника. От вет ы: а) 6; б) 12; в) 4; ? О А2 Ап β А А1 г) 8; г) 10 д) 20; е) 5. 7. п 360 0 Т – тест. • • • • Задание на карточках. Работу выполнить на листочках. Время выполнения ограничено. Критерии оценки: «5» - 9 вопросов. «4» - 7-8 вопросов. «3» - 5-6 вопросов. «2» - менее 5 вопросов. Площадь правильного п-угольника ОА – радиус описанной окружност и ( R ). ОН – радиус вписанной окружност и ( r ) D Е О F С АВ – ст орона правильного п-угольника ( ап ) S - площадь правильного многоугольника Р - перимет р В Н 1 S Pr 2 А Сторона многоугольника и радиус вписанной окружности. ОА – радиус описанной окружност и ( R ). ОН – радиус вписанной окружност и ( r ) D Е О F правильного С АВ – ст орона п-угольника ( ап ) 3600 АОВ п 1800 АОН п 180 ап 2 R sin n 0 В Н А 180 r R cos n 0 180 ап 2 R sin n 0 п = 3 0 180 3 0 а3 2 R sin 2 R sin 60 2 R R 3 3 2 п = 4 180 0 2 0 а4 2 R sin 2 R sin 45 2 R R 2 4 2 п = 6 0 180 1 0 а6 2 R sin 2 R sin 30 2 R R 6 2 Домашнее задание: Пп. 105 – 108; № 1087; № 1088 – подгот овит ь таблицу. 180 ап 2 R sin n 0 n = 4 R r 3√2 3 2√2 180 r R cos n a4 0 1 S Pr 2 P S 6 24 32 2 4 16 16 4 2√2 4√2 16√2 32 3,5√2 3,5 7 28 49 2√2 2 4 16 16