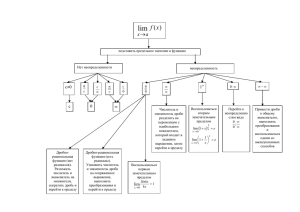
Связь предела и предельной точки
реклама

Дистанционный курс высшей математики НИЯУ МИФИ Математический анализ 1 семестр Лекция 3 Предел числовой последовательности. 25 сентября 2014 года Лектор: Доцент НИЯУ МИФИ, к.ф.-м.н. Гришин Сергей Анатольевич Основные определения, примеры Def Последовательностью a n называют числовую функцию, заданную на множестве N натуральных чисел: f n N a n f (n) Способы задания: an an 3n 2 (1) n 1 n n cos 3 n 1 (2) a n n (3) an1 an d a n (1) n n (4) an1 qan (6) an f a1 , a2 ,..., an1 (7) (5) m an , n N Основные определения, примеры Def. Последовательность a n называют ограниченной сверху (снизу), если существует константа M ( m), для которой an M n N m an , n N Если последовательность ограничена сверху и снизу, то она называется ограниченной. Def. Последовательность a n называют монотонно возрастающей ( убывающей), если a n a n1 a n a n1 n N Если неравенства строгие, то монотонность строгая. Основные определения, примеры 3n 2 (1) Пример 1 a n n 1 3n 1 1 1 an 3 - строго возрастает и ограничена n 1 n 1 n n cos 3 (2) Пример 2 a n n 1 a6k 6k 6k 1 a6 k 4 a6 k 1 6k 4 2(6k 5) Пример 3 6k 1 2(6k 2) a 6 k 5 6k 5 2(6k 6) a6 k 2 6k 2 2(6k 3) a6 k 3 6k 3 (6k 4) - ограниченная, не монотонная a n n (3) - ограниченная снизу, монотонная Основные определения, примеры n a ( 1 ) n (4) - неограниченная ни сверху, Пример 4 n ни снизу, не монотонная a 2k a 2k 1 2k Пример 5 2 k 1 an1 an d (5) - арифметическая прогрессия a n a1 d n 1 При d>0 монотонно растет, ограничена снизу При d<0 монотонно убывает, ограничена сверху. Пример 6 an1 qan (6) a n a1 q n 1 При q<0 не монотонная, ограниченная при q 1 Основные определения, примеры def Окрестностью точки x 0 радиуса называют множество U ( x0 ) x R; x x0 Выколотая окрестность точки: U ( x0 ) U ( x0 ) \ x0 0 def Число B называется предельной точкой a n , если для любого 0 окрестность U (B) содержит бесконечное число членов последовательности. def Число A называется пределом a n , если для любого 0 окрестность U (A) содержит все члены последовательности, кроме конечного их числа. А lim a n 0 n : n n an A n Теорема о существовании предельной точки Т.1. Всякая ограниченная последовательность имеет предельную точку. Док. отрезок an c1 ; b1 , n Алгоритм деления пополам: 0 N N : n N cn ; bn U B Связь предела и предельной точки Т.2. Любая предельная точка последовательности является пределом для ее подпоследовательности. Док. 1 ank U B lim ank B k k Т.3. Если последовательность имеет предел, то он единственный. Док. Пусть пределов два. В одной из окрестностей конечное число членов последовательности. Связь предела и предельной точки Вопрос 1. Может ли сходящаяся последовательность иметь две предельные точки? . Ответ: нет Если предельных точек две a и b, то 0, N m N , n N : am a Вопрос 2. 2 , an b 2 am an a b a b 2 Всякая ли последовательность, имеющая одну предельную точку, сходится? an 1 1 n n a 0 предельная точка, последовательность неограниченная Сходящиеся последовательности Т.4. Всякая сходящаяся последовательность ограничена. Док. Все члены последовательности, кроме конечного их числа, принадлежат окрестности предела – ограниченному множеству. Т.5. Всякая возрастающая, ограниченная сверху последовательность имеет предел. Док. Всякая возрастающая, ограниченная сверху последовательность ограничена, поэтому имеет предельную точку A. Если A предельная точка, то an A n и 0 N N : A a N A Тогда n N A a N an A an A Фундаментальные последовательности Def Последовательность a n называется фундаментальной, если 0 N N : n, m N an am Свойство 1. Фундаментальная последовательность ограничена. Пусть m0 N . Тогда множество членов последовательности a n с номерами n N ограничено, поскольку am0 an am0 . Свойство 2. Предельная точка фундаментальной последовательности является пределом. Пусть A – предельная точка: 0 m0 N : a m A 0 2 Последовательность фундаментальная: n N a n a m 0 Объединение: a n A a n a m0 a m0 A a n a m0 a m0 A 2 2 2 Фундаментальные последовательности Свойство 3. Фундаментальная последовательность сходится. Свойство 1 ограниченная имеет предельную точку Свойство 2 имеет предел Свойство 4. Сходящаяся последовательность фундаментальна. сходимость 0 N N : n, m N a n A 2 , am A Объединение: an am an A A am an A am A фундаментальность 2 2 2 Справочник 1 ~ называется точной верхней гранью числового Def Число M ~ 2) 0 x X : x M ~ множества X, если 1) x X x M ~ Обозначение M sup X ~ называется точной нижней гранью числового Def Число m ~ ~ 2) 0 x X : x m множества X, если 1) x X x m ~ inf X Обозначение m Факт 1 Любое ограниченное числовое множество X имеет sup X и inf X Пусть B – множество предельных точек последовательности Def Верхним пределом a n , обозначение называют число, равное sup B ___ lim a n n a n Справочник 2 Def Нижним пределом a n , обозначение lim an ___ n называют число, равное inf B Факт 2 Всякая ограниченная сверху последовательность ___ имеет lim a n n Всякая ограниченная снизу последовательность an имеет lim ___ n Факт 3 Верхний и нижний пределы последовательности являются ее предельными точками. ___ Факт 4 Условие lim a n lim an необходимое и достаточное для n ___ n сходимости последовательности a n Теоретические упражнения Упражнение 1 Придумайте расходящуюся последовательность с единственной предельной точкой. Пример. 1 , b2 n 1 n n B 0 предельная точка, последовательность bk неограничена, b2 n расходится Упражнение 2 Придумайте пример последовательности с тремя предельными точками. Теоретические упражнения 1 1 1 c3k 1 , c3k 1 2 , c3k 2 3 k k k Упражнение 3 Множество рациональных чисел счетное, поэтому всех их можно объединить в одну последовательность. Какое множество предельных точек такой последовательности? Любое действительное число a - предельная точка последовательности рациональных чисел: 1 k N k Q : a k lim k a k k Вопросы к экзамену 1) Последовательности и способы их задания, примеры. Ограниченные, монотонные последовательности. Предельные точки последовательности. Теорема о существовании предельных точек. 2) Предел последовательности. Теорема о единственности предела. Теорема об ограниченности сходящейся последовательности. 3) Подпоследовательности. Предельная точка как предел сходящейся подпоследовательности 4) Теорема о существовании предела монотонной, ограниченной последовательности. Дистанционный курс общей физики НИЯУ МИФИ Математический анализ. Предел числовой последовательности. Лекция 3 Завершена. Спасибо за внимание! Тема следующей лекции: Раскрытие неопределенности для последовательности. Лекция состоится в четверг 2 октября в 10:00 по Московскому времени.