Интегральное исчисление. Прикладные задачи

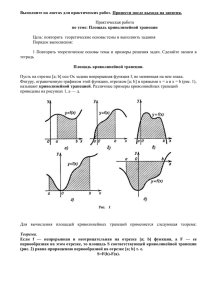
Интегральное
исчисление.
Прикладные задачи
1.Площадь криволинейной трапеции
y
y=f(x)
Для вычисления площади
криволинейной трапеции
используют следующую
формулу:
0
a
b
x
b
S   f(x)dx  F(b) - F(a),
a
где F(x) – первообразная функции y=f(x).
Криволинейная трапеция
Пример 1. Найти площадь фигуры, ограниченной кривыми
y
y  x , y  x2 .
y  x2
y
Произведем
соответствующие
построения.
1
0
1
S
0

x
x
1
1
3


2 1 1
2 2 1 3
2
x  x dx   x  x     .
3 
3 3 3
3

0
Ответ. 1/3 кв.ед.

2. Приложения в механике
Интегрирование – операция, обратная дифференцированию,
поэтому
- зная закон скорости движения, с помощью
интегрирования можно восстановить сам закон движения;
- зная закон ускорения, с помощью
можно определить скорость;
интегрирования
Таким образом, если x(t) – закон движения материальной точки,
v(t) – скорость движения, a(t) – ускорение, то
x(t)   v(t)dt ;
v (t )   a(t)dt.
Пример 2. Найти закон движения материальной точки, если
известно, что в начальный момент времени его координата была
равна 0, в момент времени t=3 его скорость была равна 10м/с.
Тело двигалось с постоянным ускорением, равным 2м/с.
По условию известно, что x(0)=0; v(3)=10; a=2.
v(t )   a(t)dt  2dt 2t  C1;
10  2  3  C1  C1  4  v(t )  2t  4.
2t 2
x(t )   v(t)dt   (2t  4)dt 
 4t  C2  t 2  4t  C2 ;
2
0  02  4  0  C2  C2  0  x(t)  t 2  4t.
Ответ.
x(t)  t 2  4t.