Дидактика к курсу

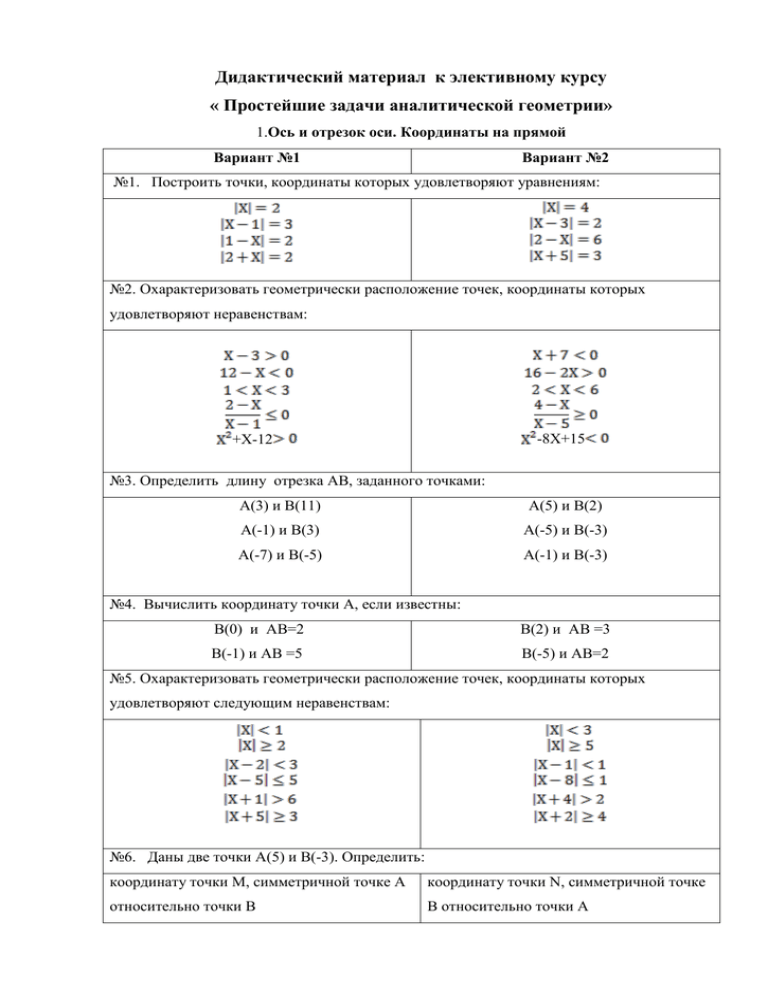
Дидактический материал к элективному курсу
« Простейшие задачи аналитической геометрии»
1.Ось и отрезок оси. Координаты на прямой
Вариант №1
Вариант №2
№1. Построить точки, координаты которых удовлетворяют уравнениям:
№2. Охарактеризовать геометрически расположение точек, координаты которых
удовлетворяют неравенствам:
+Х-12
-8Х+15
№3. Определить длину отрезка АВ, заданного точками:
А(3) и В(11)
А(5) и В(2)
А(-1) и В(3)
А(-5) и В(-3)
А(-7) и В(-5)
А(-1) и В(-3)
№4. Вычислить координату точки А, если известны:
B(0) и AB=2
В(2) и AB =3
В(-1) и AB =5
В(-5) и AB=2
№5. Охарактеризовать геометрически расположение точек, координаты которых
удовлетворяют следующим неравенствам:
№6. Даны две точки А(5) и В(-3). Определить:
координату точки M, симметричной точке А
координату точки N, симметричной точке
относительно точки В
В относительно точки А
2. Декартовы прямоугольные координаты на плоскости
Вариант №1
Вариант №2
№1.Найти координаты проекций на ось
абсцисс точек:
А (2; 3), B(3; -1), C(-5; 1), D(-3; 2), E(-5; -1).
№2. Найти координаты точек,
симметричных относительно оси ОХ
точкам: А(2; 3); B(-3; 2);
C(-1; -1); D(-3; -5);
E(-4; -6); F(a, b);
№1.Найти координаты проекций на ось
ординат точек:
А(-3; 2), B(-5; 1), C(3; -2), D(-1; 1), E(-6; -2).
№2. Найти координаты точек,
симметричных относительно оси ОУ
точкам: А(2; 3); B(-3; 2);
C(-1; -1); D(-3; -5);
E(-4; -6); F(a, b);
№3. Определить, в каких четвертях может быть расположена точка М(x; y), если:
xy>0
xy<0;
x-y=0;
x +y=0;
x +y>0
x +y<0;
x - y>0;
x -y<0;
№4. Найти координаты точек симметричных относительно начала координат точкам:
A(3; 3);
A(6; 6);
B(2; -4);
B(3; -7);
C(-2; 1);
C(-3; 1);
D(5; -3);
D(8; -3);
E(-5; -4);
E(-3; -5);
F(a; b);
F(a; b);
3. Отрезок, его проекции, длина. Расстояние между двумя точками
Вариант №1
Вариант №2
№1. Построить на чертеже отрезки, исходящие из начала координат, зная их проекции на
координатные оси:
X=3, Y=2;
X=2, Y=-5;
X=-5, Y=0;
X=-2, Y=3;
X=0, Y=3;
X=-5, Y=-1;
№2. Построить на чертеже отрезки, имеющие началом точку M(2; -1), зная их проекции
на координатные оси:
X=4. Y=3;
X=-4, Y=-2;
X=2, Y=0;
X=0, Y=-3;
X=-3, Y=1;
X=1, Y=-3.
№3. Даны проекции X=5, Y=-5 отрезка
№3. Даны проекции X=4, Y=-5 отрезка
на координатные оси; зная, что его
начало в точке М1(-2; 3), найти координаты
его конца.
на координатные оси; зная, что его конец в
точке B(1; -3), найти координаты его
начала.
№4.Даны точки A(0; 0), B(3; -4), C(-3; 4), D(-2; 2), E(10; -3). Определить расстояние d
между точками:
А и В.
C и D.
В и С.
A и D.
АиС
D и E.
№5. На оси абсцисс найти такую точку М,
№5. На оси ординат найти такую точку М,
расстояние от которой до точки N(2; -3)
расстояние от которой до точки N(-8; 13)
равнялось бы 5.
равнялось бы 17.
4. Деление отрезка в данном отношении
Вариант №1
Вариант №2
№1. Даны вершины треугольника. Определить середины его сторон.
А(1; -3), В(3; -5), С(-5; 7).
№2. Точки А(2; -1), N (-1; 4), P(-2; 2)
являются серединами сторон
А(2; -5), В(3; -2), С(-4; 6).
№2. Даны три вершины параллелограмма
А(3; -5), B(5; -3), C(-1; 3). Определить
четвертую вершину D, противоположную B
треугольника. Определить его вершины.
№3. Даны две смежные вершины
№3.Даны вершины треугольника A(1; 4),
параллелограмма А(-3; 5), B(1; 7) и точка
B(3;-9), C(-5; 2). Определить длину его
пересечения его диагоналей M(1; 1).
медианы, проведенной из вершины B.
Определить две другие вершины.
№4. Даны три вершины А(2; 3), B(4; -1),
№4. Даны вершины треугольника
C(0;5) параллелограмма ABCD. Найти его
A(2; -5), B(1; -2), C(4; 7). Найти точку
четвертую вершину D.
пересечения биссектрисы его внутреннего
угла при вершине В со стороной АС.
№5. Прямая проходит через точки
M1(-12; -13), M2(-2; -5). На этой прямой
найти точку, абсцисса которой равна 3.
№5. Прямая проходит через точки
M(2; -3),N(-6, 5). На этой прямой найти
точку, ордината которой равна –5.
№6.Даны вершины четырехугольника А(-3;
№6.Даны вершины четырехугольника A(-2;
12), B(3; -4), C(5; -4), D(5; 8). Определить, в
14), B(4; -2), C(6; -2), D(6; 10). Определить
каком отношении его диагональ AC делит
точку пересечения его диагоналей AC и BD.
диагональ BD.
5. Площадь треугольника
Вариант №1
Вариант №2
№1. Вычислить площадь треугольника, вершинами которого являются точки:
A(2; -3), B(3; 2), C(-2; 5);
№2. Площадь треугольника S=3, две его
вершины точки A(3; 1), B(1; -3), а третья
вершина С лежит на оси OУ. Определить
M1(-3; 2), M2(5; -2), M3(1; 3);
№2. Площадь треугольника S=4, две его
вершины точки А(2; 1), B(3; -2), а третья
вершина С лежит на оси OХ. Определить
координаты вершины С.
координаты вершины С.
№3. Площадь параллелограмма S=12; две
№3. Площадь параллелограмма S=17; две
его вершины точки A(-1; 3), B(-2; 4). Найти
его вершины точки A(2; 1), B(5; -3). Найти
две другие вершины этого параллелограмма две другие вершины этого параллелограмма
при условии, что точка пересечения его
при условии, что точка пересечения его
диагоналей лежит на оси абсцисс.
диагоналей лежит на оси ординат.
6.Общее уравнение прямой. Уравнение прямой угловым
коэффициентом. Угол между двумя прямыми
Вариант №1
№1. Точки P1, P2, P3, P4, P5 расположены на
прямой3х-2y-6=0; их абсциссы
соответственно равны числам 4; 0; 2; -2; -6.
Определить ординаты этих точек.
№2. Стороны АВ, ВС и АС треугольника
АВС даны соответственно уравнениями
4х+3y-5=0, х-3y+10=0 , х-2=0 .
Определить координаты его вершин.
Вариант №2
№1. Точки Q1, Q2, Q3, Q4, Q5 расположены
на прямой х-3y+2=0; их ординаты
соответственно равны числам 1; 0; 2; -1, 3.
Определить абсциссы этих точек.
№2. Даны уравнения двух сторон
параллелограмма8х+3y+1=0, 2х+y-1=- и
уравнение одной из его диагоналей
3х+2y+3=0. Определить координаты
вершин этого параллелограмма.
№3. Составить уравнение прямой и построить прямую на чертеже, зная ее угловой
коэффициент k и отрезок b, отсекаемый ею на оси OY:
k=2/3, b=3;
k=-3/4, b=3;
k=3, b=0;
k=-2, b=-5;
k=0, b=-2;
k=-1/3, b=2/3
№4. Определить угловой коэффициент k и отрезок b, отсекаемый на оси Oy, для каждой
из прямых:
5х-y+3=0
5х+3y+2=0
2х+3y-6=0
3х+2y=0
№5. Дана прямая 5х+3y-3=0. Определить угловой коэффициент k прямой:
Параллельной данной прямой;
Перпендикулярно к данной прямой
№6. Дана прямая 2х+3y+4=0. Составить уравнение прямой, проходящей через точку
М0(2; 1):
Перпендикулярно к данной прямой
№7. Определить угол между двумя прямыми:
Параллельной данной прямой
7. Неполные уравнения прямой. Уравнение прямой "в отрезках"
Вариант №1
Вариант №2
№1 Даны прямые. Составить для них уравнения «в отрезках» и построить эти прямые на
чертеже.
№2.Составить уравнение прямой, которая
№2. Составить уравнение прямой, которая
проходит через точку С(1; 1) и отсекает от
проходит через точку В(5; -5) и отсекает от
координатного угла треугольник с
координатного угла треугольник с
площадью, равно 2.
площадью, равной 50.
8. Нормальное уравнение прямой. Расстояние от точки до прямой.
Расстояние между параллельными прямыми.
Вариант №1
Вариант №2
№1. Определить, какие из следующих уравнений прямых являются нормальными:
№2. Привести общее уравнение прямой к нормальному виду в каждом из следующих
случаев:
№3. Доказать, что прямая
№3.Доказать, что прямая
не
пересекает отрезок, ограниченный точками
пересекает отрезка, ограниченного точками
А(-5; 1), В(3; 7).
M1(-2; -3), M2(1; -2).
№4. Вычислить расстояние d между параллельными прямыми в каждом из следующих
случаев:
№5. Доказать, что через точку Р(2; 7) можно
№5. Доказать, что через точку Р(2; 5)
провести две прямые так, чтобы их
можно провести две прямые так, чтобы их
расстояния от точки Q(1; 2) были равны 5.
расстояния от точки Q(5; 1) были равны 3.
Составить уравнения этих прямых.
Составить уравнения этих прямых.
Проверочная работа
Вариант №1
Вариант №2
Даны точки М(1;2), N(-3;4)
Даны точки М(1;1), N(2;-2)
1. Напишите общее уравнение прямой МN
2. Напишите уравнение прямой М N
a) с угловым коэффициентом;
b) в отрезках.
3. Напишите уравнение:
a) прямой КF, параллельной MN и проходящей через точку К (-2;-1), и укажите
какую- либо точку F этой прямой, отличной от К;
b) прямой АВ, проходящей через начало координат и перпендикулярно MN
4. Вычислите:
a) площадь треугольника MNF;
b) расстояние между прямыми KF и MN.
Тест
Вариант№1
1. Точки А и В имеют координаты А(-3;-1); В(2;-4).Найдите отрезок АВ.
a)
b) 5
c)
d) 8
2. ABCD- параллелограмм. Координаты его вершин А (-3;-1), В(-2;4), С (6;-1). Найдите
координаты (x;y) вершины D. В ответе запишите х+у.
a) 3
b) -3
c) -1
d) 1
3. Дан треугольник MPK. Точка М (-5;-3), P(-3;5),К (5;-1). Найдите длину медианы РС.
a) 7
b)
c)
d)
4.Запишите уравнение прямой АВ, если А (-3;4), В (-1;-2).
a) у=3х-2
b) у=-2х+3
c) у=2х+3
d) у=-3х-5
5.Даны уравнения двух прямых :-2х-7у+1=0 и 3х+4у+5=0.Найдите координаты (х0;у0)
точки пересечения этих прямых. В ответе запишите сумму х0+у0
a) -2
b) 2
c) -1
d) 1
Вариант№2
1. Точки M и Nимеют координаты M(3;-2); N(-1;3).Найдите отрезок MN.
a) 6
b)
c) 9
d)
2. ABCD- параллелограмм. Координаты его вершин B (-3;2), C(7;-1), D (6;-5). Найдите
координаты (x;y) вершины A. В ответе запишите х + у.
a) 5
b) -2
c) -6
d) 3
3. Дан треугольник CDE. Точка C (-5;2), D(4;3),E(1;-4). Найдите длину медианы DK.
a) 6
b)
c)
d) 8
4.Запишите уравнение прямой CD, если C (-3;1), D (-5;9).
a) У =4х+5
b) у= 3х+5
c) у =-4х-11
d) у=-3х+8
5.Даны уравнения двух прямых :-3х-у+1=0 и 4х+3у+7=0.Найдите координаты (х0;у0) точки
пересечения этих прямых. В ответе запишите сумму х0+у0/
a) 5
b) 3
c) -3
d) -5