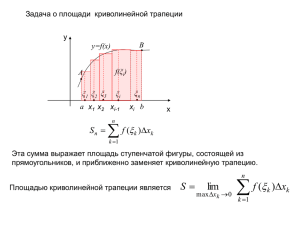
функции y=f(x)

Определенный интеграл с переменным верхним пределом.
y=f(x) интегрируема на [a, b] тогда она
интегрируема на любом отрезке [a, x], где a ≤ x ≤ b и имеет смысл
Опр. 2. Пусть функция
интеграл
x

f (t )dt  J ( x)
(2)
a
J(x) определена на [a, b] и называется интегралом с переменным
верхним пределом.
Теорема 5. Пусть функция
b]. Определенный
интеграл с переменным верхним пределом от непрерывной на [a, b]
функции y=f(x) является первообразной для подынтегральной
функции f(x)
то есть
y=f(x) непрерывна
на [a,
J ( x)  f ( x) x  [a, b] ( 3 )
x
(Или функция

J ( x)  f (t )dt
a
имеет производную
x  [a, b]
причем
J ( x)  f ( x))
Следствие
Теорема 5*. Всякая непренывная функция имеет непрерывную
первообразную
Формула Ньютона-Лейбница (основная теорема
интегрального исчисления, связывает сумму Римана
– определенный интеграл с первообразной)
Сэр Исаа́к Нью́тон (4 января 1643 — 31 марта 1727) —
английский физик, математик и астроном, один из
создателей классической физики. Разработал
дифференциальное и интегральное исчисление.
Из сохранившихся документов историки науки выяснили,
что дифференциальное и интегральное исчисление
Ньютон открыл ещё в 1665-1666 годы, однако не
публиковал его до 1704 года.
Готфрид Вильгельм фон Лейбниц (1646) разработал
свой вариант анализа независимо (с 1675 года), хотя
первоначальный толчок, вероятно, его мысль
получила из слухов о том, что такое исчисление у
Ньютона уже имеется, а также благодаря научным
беседам в Англии и переписке с Ньютоном. В отличие
от Ньютона, Лейбниц опубликовал свою версию, и в
дальнейшем, вместе с Якобом и Иоганном Бернулли,
широко пропагандировал это эпохальное открытие по
всей Европе. Большинство учёных на континенте не
сомневались, что анализ открыл Лейбниц.
Теорема 6. (Ньютона-Лебница)
Если F(x)
- какая-либо первообразная
от непрерывной функции y=f(x) , то справедлива формула
b
 f ( x)dx  F ( x)
b
a
 F (b)  F (a)
(4)
a
b
a
- знак подстановки. Читают
F(x)
от
a
до
b.
Замечание. Формула Ньютона-Лейбница справедлива и для кусочнонепрерывных функций.
Методы вычисления определенного интеграл
- Табличное
b
- Интегрирование по частям
 UdV  UV
b
b
a
a
- Интегрирование методом подстановки
Теорема 7. Пусть функция
b
y=f(x) непрерывна
  VdU
a
на [a,
b] и дан интеграл
 f ( x)dx
a
Введем новую переменную
Если
1)
2)
3)
t по формуле x = j (t)
j(a) = a, j (b) = b
j(t) и j'(t) непрерывны на [ a, b ]
f [j (t)] определена и непрерывна на [a, b ] то
b
b

a
f ( x)dx 

a
f (j (t ))j (t )d t
Интегралы по симметричному промежутку от четной и нечетной функции.
Теорема 7. Пусть
a

y=f(x) непрерывная четная
на [- a, a] функция, тогда
y
a

f(x)
f ( x)dx  2 f ( x)dx
a
S1
0
S2
-a
Теорема 8. Пусть
y=f(x) непрерывная нечетная
a
на [- a,

a
a] функция, тогда
y
a
f ( x)dx  0
f(x)
-a
S+
a x
S-
x