Геометрия Планиметрия (от греч. – наука о
реклама

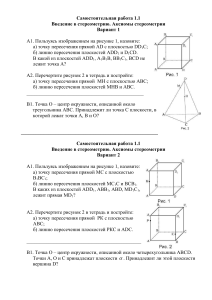
Геометрия (от греч. «землемерие») – наука о свойствах геометрических фигур. Планиметрия – раздел геометрии, в котором изучаются свойства фигур на плоскости. Основные понятия планиметрии: точка и прямая. m M Стереометрия – раздел геометрии, в котором изучается свойства фигур в пространстве Основные понятия стереометрии А а КУБ Тетраэдр B1 D C1 A1 D1 В С А D В1 A C B ПАРАЛЛЕЛЕПИПЕД С1 А1 D1 С В А D АКСИОМЫ СТЕРЕОМЕТРИИ А 1 :Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. В А С А 2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. В А А 3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. а Т 1: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Дано: а ,М а Док-ть: (а, М) Q Р а М Док-во: 1. Р а, Q а 2.Точки М, Р и Q не лежат на одной прямой (по А 1) 3. По А1 эта плоскость единственная. чтд Т 2: Через две пересекающиеся прямые проходит плоскость, и притом только одна. Дано: а b = М Док-ть: (а, b) а N b M Док-во: 1. N b, М N 2. (N, а) ( по Т 1) 3. Т.к. М , N b (по А 2) (а, b) 4. Любая плоскость, проходящая через а и b, проходит через N, т.е. совпадает с единственность плоскости. чтд Аксиомы стереометрии ABCD - параллелограмм АМ = MD, AK = КВ AD = 14 А К Е D В 1. Построить М С точку пересечения прямой МК и плоскости . 2. Вычислить расстояние от этой точки до точек В и С. Аксиомы стереометрии Точки А, В, С и К не лежат в одной плоскости. К А С В 1. Пересекаются ли прямые АС и ВК? 2. Лежат ли в одной плоскости точки А, К, В? 3. Пересекает ли прямая АС плоскость КВС? Аксиомы стереометрии В пересекающихся плоскостях и взяты соответственно точки А и В, которые не лежат на линии их пересечения (прямой с). Точка М лежит на прямой с. А М с В 1. Построить линию пересечения плоскостей и (МАВ). 2. Построить линию пересечения плоскостей и (МАВ). Задача 1. ABCD – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки A, D, O лежат на плоскости . M Дайте ответы на вопросы с необходимыми обоснованиями. 1. Лежат ли в плоскости точки В и С? 2. Лежит ли в плоскости МОВ точка D? 3. Назовите линию пересечения плоскостей МОВ и ADO. D 60 А 4 С О В 4. Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 60. Предложите различные способы вычисления площади ромба. Задача 2. Дан тетраэдр МАВС, каждое ребро которого равно 6 см. D МВ, Е МС, F АВ, AF = FB, P МА. 1. Назовите прямую, по которой пересекаются плоскости: а) МАВ и MFC; М б) MCF и ABC. 2. Найти длину отрезка CF и площадь треугольника АВС. АВС – равносторонний, F – середина АВ. P 6 DE ВМС, ВС ВМС DE ВС = К F Е 3. а) Объясните, как построить точку пересечения прямой DE с плоскостью АВС. А б) Постройте точку пересечения прямой PD с плоскостью АВС. К D С 6 В PD АВС = R R Задача 3. АВCDА1В1С1D1 - куб, К DD1, DK = KD1. 1. Как построить точку пересечения прямой В1К с плоскостью АВС. 2. Объясните, как построить линию пересечения плоскостей АВ1К и ADD1. Решение: 1. AKD (D = 90) АК = 5 2 2. АВВ1 (В = 90), АВ = ВВ1 = а АВ1 = а 2 D1 В А АК2 = AD2 + KD2 ( по теореме Пифагора) а С1 А1 3. Объясните, как построить линию пересечения плоскостей АВ1К и ADC. 4. Вычислите длины отрезков АК и АВ1, если AD = а В1 К С а D P