Муниципальное бюджетное общеобразовательное учреждение центр образования «Альянс» п.Харик Куйтунского района Иркутской области

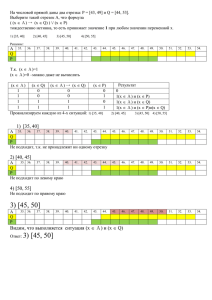
Муниципальное бюджетное общеобразовательное
учреждение центр образования «Альянс» п.Харик
Куйтунского района Иркутской области
Учебный проект по математике.
«Тригонометрия помощница алгебры
или как решить задание С1 ЕГЭ»
Автор: Сиренченко Дарья(11 кл)
Преподаватель: Марченко Т.А.
201 5г.
Решите уравнение
2cos²x=√3sinx(3 /2-x).
Укажите корни,
принадлежащие отрезку
[- /2; ]
www.themegallery.com
Company Logo
Проблема:
Как указать корни решённого
тригонометрического уравнения,
принадлежащие заданному отрезку?
www.themegallery.com
Company Logo
Узнать, кто из ученых начиная с XVI века внес вклад
в развитие тригонометрии и как указать корни
решённого
тригонометрического
уравнения,
принадлежащие заданному отрезку?
Задачи:
1.Познакомиться с историей возникновения тригонометрии.
2.Узнать статистические данные в разрезе России, области,
района
по данным решения задания С1
3.Изучить способы с помощью которых можно указать корни
решённого тригонометрического уравнения, принадлежащие
заданному отрезку.
4.Найти рациональные способы решения второй части задания С1
для различных случаев.
Франсуа Виет дополнил и
систематизировал
различные случаи решения
плоских и сферических
треугольников, открыл
формулы для
тригонометрических
функций от кратных углов.
Исаак Ньютон
разложил
тригонометрические
функции в ряды и
открыл путь для их
использования в
математическом
анализе.
Самый значительный
вклад в развитие
тригонометрии внес
швейцарский
математик и механик,
академик
Петербургской
Академии наук
Леонард Эйлер.
Эйлер ввел и само понятие
функции и принятую в наши дни
символику.
Он придал всей тригонометрии
ее современный вид.
Величины sin x, cos x
рассматривал как функции
числа х – радианной меры
соответствующего угла.
Он ввел обратные
тригонометрические функции.
Такой замечательный
факт, как то, что любую
периодическую функцию
можно представить с
наперед заданной
точностью как сумму
синусов, обнаружил еще в
XVIII веке Д. Бернулли
при решении задачи о
колебании струны.
Систематические
разложения
периодических функций в
сумму синусов (или, как
говорят, на гармоники)
изучал в начале XIX века
французский математик
Жан-Батист-Жозеф
Фурье. Эти разложения
так теперь и называются
рядами Фурье.
Данные по России:
2012 год
2013 год
Приступили к
решению С
58,92%
72%
Не приступили к
решению
41,08%
28%
Приступили, но
получили 0 баллов
27,8%
27,4%
Получили 1балл
13,53%
10,1%
Получили 2 балла
17,58%
34,5%
www.themegallery.com
Company Logo
Данные по области:
2012 год
2013 год
Приступили к
решению С
46,7%
44,6%
Не приступили к
решению
52,4%
55,4%
Приступили, но
получили 0 баллов
25,1%
24,3%
Получили 1балл
8,9%
5,7%
Получили 2 балла
13,6%
14,6%
www.themegallery.com
Company Logo
Данные по району:
(диагностическая работа, декабрь)
2012 год
2013 год
Приступили к
решению С
Не приступили к
решению
Приступили, но
получили 0 баллов
Получили 1балл
Получили 2 балла
www.themegallery.com
Company Logo
Решите уравнение 2cos²x=√3sinx(3 /2-x).Укажите
корни, принадлежащие отрезку [- /2; ]
a)2cos²x=√3sin(3 /2-x)
1.Определяем знак синуса.Так как sin находится в третьей
четверти, ставим знак минус. Угол равен 270˚, значит название
функции меняем на cos.
Отсюда получаем уравнение:
2cos²x=-√3cosx
3.Находим корни уравнения:
2cos²x+√3cosx=0
cosx (2cosx+√3)=0
1корень:
2 корень:
cosx=0
2cosx+√3=0
x= /2+ k,k Є z.
2cosx=-√3
cosx=-√3/2
X1,2=±( -arccos√3/2)+2 n,n Єz
X1,2=± 5 /6+2 n,n Єz
Решите уравнение 2cos²x=√3sinx(3 /2x).Укажите корни, принадлежащие
отрезку [- /2; ]
б)Находим корни, принадлежащие отрезку (- /2; )
Первый способ:
Способ подстановки.
1 корень: x= /2+ k,k Є z
Возьмём k=0, x= /2(принадлежит отрезку)
k=0, x=3 /2(не принадлежит отрезку, т.к. 3 /2> )
k=-1, x=- /2(принадлежит отрезку)
k=-2, x=-3 /2(не принадлежит отрезку, т.к -3 /2<- /2)
Решение с помощью
подстановки.
2 корень: X1=5 /6+2 n,n Єz
Возьмём n=0, x=5 /6 (принадлежит отрезку)
n=1, x=17 /6 (не принадлежит отрезку, т.к.
17 /6> )
n=-1, x=-7 /6 (не принадлежит отрезку, т.к. 7 /6<- /2)
X2=-5 /6+2 n,n Єz
n=0, x=-5 /6 (не принадлежит отрезку)
n=1, x=7 /6 не принадлежит отрезку)
Ответ: а) /2+ k,k Єz ; ±5 /6+2 n,n Єz
б)- /2; /2; 5 /6
Решение с помощью
окружности.
Чертим единичную окружность. Проводим
прямую x=-√3/2. Ищем точки, входящие в
интервал[- /2; ]
Решение с помощью
окружности.
2 точка не входит в отрезок. Ищем
значение для первой точки: -arccos(√3/2)= -arccos√3/2= - /6=5 /6
Решение с использованием
графика функции у=COSX
Решение с помощью графика.
Проводим прямую x приблизительно
равную -0,8.
По графику видно, что в отрезок входит
одна точка
x= - /6=5 /6
1. Я изучила и узнала, что Франсуа Виет, Исаак
Ньютон, Леонард Эйлер, Д.Бернулли, ЖанБатист-Жозеф Фурье внесли большой вклад
в развитие тригонометрии.
2. Узнала, что при решении тригонометрических
уравнений можно применять три способа
определения
корней
принадлежащих
заданному промежутку;
3. Научилась выбирать наиболее рациональный
способ нахождения корней принадлежащих
заданному промежутку.





Энциклопедия для детей. Т.11. Математика. Главный
редактор М.Д. Аксенова.- М:Аванта+,1999.-688с.: ил.
Математика: Школьная энциклопедия. Гл. ред. С. М.
Никольский. – М.: Большая Российская энциклопедия;
Дрофа, 1997. – 527 с.: ил.
Башмаков М. И. Алгебра и начала анализа. Учебник для
10-11 классов средней школы. – М.: Просвещение, 1993.
– 352с.
Колмогоров А. Н. Алгебра и начала анализа. Учебник
для 10-11 классов средней школы. – М.: Просвещение,
1990. – 320с.
Савин А. П. Энциклопедический словарь юного
математика. – М.: Педагогика, 1989 – 352 с.: ил.