Лабараторная. Интерполирование функций. Вариант 2

Лабораторная работа 1. Интерполирование функций.
Цель
работы:
изучение
методов
интерполирования
функций,
написание и выполнение программы интерполирования функции методом
Лагранжа.
Описание метода Лагранжа.
Интерполирование предполагает нахождение
значений функции,
соответствующих промежуточным значениям аргумента, отсутствующим в
таблице логарифмов, тригонометрических и др. функций.
При интерполировании по таблице значений функции строится ее
аналитическое выражение, т.е. по значениям функции y0, y1, ..., yn при
значениях аргумента хо, х1, ..., хn определяется выражение неизвестной
функции. Через данные точки можно провести множество различных
кривых. Поэтому существует интерполирование в различных функциях F(х).
Чаще всего требуется, чтобы функция F(х) была многочленом степени на
единицу меньшей, чем число известных значений.
Таким
образом,
задачу
интерполирования
функций
можно
сформулировать следующим образом.
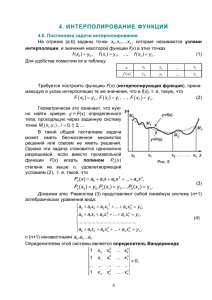
Для данных значений х  хо, х1, ..., хn и y  y0, y1, ..., yn найти многочлен
y = Fn(х), удовлетворяющий условиям F(хо)  y0, F(х1)  y1, ..., F(хn)  yn.
Точки хо, х1, ..., хn называют узлами интерполяции, многочлен Fn(х) 
интерполяционным
многочленом,
а
формулы
его
построения

интерполяционными формулами. Интерполяционный многочлен опишет
кривую, проходящую точно через заданные точки.
При параболическом интерполировании в качестве интерполяционного
многочлена F(х) принимают многочлен n  ой степени вида:
Fn(х)  ао + а1х + а2х2 + ... + аnxn.
1
Запишем многочлен F(х) для произвольного значения хi (i = 0, 1, 2, ...,
n), принимающего значения F(хi) = yi, а во всех остальных точках х  хi
значение, равное нулю.
Fi x  
x  x0 x  x1 ...x  xi1 x  xi1 ...x  xn   y
xi  x0 xi  x1 ...xi  xi1 xi  xi1 ...xi  xn  i
Как видно из записи, числитель не будет содержать выражения (х  хi),
а знаменатель  (хi  хi), т.е. выражений, обращающих числитель и
знаменатель в нуль.
Искомый многочлен будет равен сумме
n
F  x    Fi  x 
i 0
Полученная
формула
называется
интерполяционной
формулой
Лагранжа.
Пусть r(x) – некоторая функция, w(x)=(x-x0)(x-x1)…(x-xn) тогда
формула погрешности имеет вид:
f ( n1) ( )
Rn x   r ( x) w( x) 
w( x)
(n  1)!
Блок-схема
алгоритма
программы
методом Лагранжа:
2
интерполирования
функции
Начало
Ввод данных
Повторить n раз
Повторить n раз
i<>j
Вывод итога
Вывод графика
конец
При запуске программы срабатывает алгоритм нахождения значения
интерполирующей функции в заданной точке х. Он заключается в
следующем:
for ($i = 0; $i < 20; $i++) // пробегаем по всем х и y
{
$p = 1;
for ($j=0; $j < 20; $j++)
{
if ($i != $j)
{
$p = $p*($x-$a[$j])/($a[$i]-$a[$j]); //находим коэффициент ЛаГранжа
}
3
}
$p = $p * $b[$i];
$s = $s + $p;
// находим значение интерполирующей ф-ии
}
echo "<hr /><h1>Ответ: $s</h1>"; // выводим окончательный ответ
Вариант 12.
x=9,14
xi
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
yi
-114
-77
-54
-28
-14
-4
-1
0
-1
-
-
-
3
11
28
46
74
112
159
218
2
2
1
Ответ: 268,64.
4