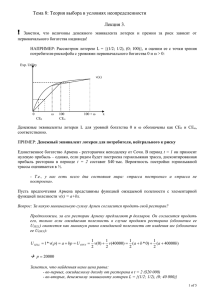
x < L
реклама

Теория выбора в условиях неопределенности - 2 Модель спроса на страховку как приложение теории ожидаемой полезности Частный случай: спрос рискофоба на актуарно справедливую страховку Контингентные блага Модель спроса на страховку в терминах контингентных благ Функция ожидаемой полезности в пространстве контингентных благ: иллюстрация отношения к риску Примеры использования теории ожидаемой полезности: модель спроса на страховку - индивид-рискофоб, предпочтения описываются функцией ожидаемой полезности - первоначальное богатство составляет w - с вероятностью p (0; 1) происходит несчастный случай - если он происходит, индивид несет потери L (0; w) - Страховая компания предлагает индивиду застраховать ущерб: - стоимость страховки: γ за каждую единицу покрытия (то есть, заплатив γx долларов, индивид, в случае наступления ущерба, получит возмещение x долларов). На какую сумму индивид застрахует свой ущерб? Индивид стремится выбрать размер покрытия x так, чтобы максимизировать свою ожидаемую полезность: max pv( w L x x ) (1 p )v ( w x ) L x 0 Поскольку индивид – рискофоб, v(.) – строго вогнутая функция. Функция ожидаемой полезности, таким образом, тоже оказывается строго вогнутой. Условия первого порядка, необходимые и достаточные для ее максимизации: pv '( w L x x )(1 ) (1 p )v '( w x ) 0, L x 0 pv '( w L x x )(1 ) (1 p )v '( w x ) 0, x 0 pv '( w L x x )(1 ) (1 p )v '( w x ) 0, x L (1) (2) (3) Несколько непривычный вид F.O.C. связан с тем, что на рынке страховых услуг запрещено страховаться на сумму, превышающую стоимость ущерба это считается мошенничеством! Так на какую же сумму индивид застрахует ущерб? Чтобы ответить, нам нужны какие-то предположения о p, γ и v(.)! Давайте рассмотрим один из наиболее важных случаев: случай актуарно справедливой страховки. Актуарно справедливой называется схема страховки, при которой цена единицы страхового покрытия равна вероятности наступления страхового случая: γ = p. В этом случае страховая компания, не имеющая иных издержек, кроме страховых выплат, имела бы нулевую прибыль при любом объеме продаваемой страховки: (γx – px = 0). Перепишем выведенные ранее условия первого порядка, заменив γ на p. Начнем с условия (1): pv '( w L x px )(1 p ) (1 p )v '( w px ) p 0, L x 0 p(1 p ) v '( w L x px ) v '( w px ) 0 v '( w L x px ) v '( w px ) Последнее равенство может выполняться только при x = L, т.к. v(.) – монотонно возрастающая функция. Но L > x >0 этот случай не является решением задачи! Теперь рассмотрим случай (2): pv '( w L)(1 p ) (1 p )v '( w) p 0, x 0 p(1 p ) v '( w L) v '( w) 0 v '( w L) v '( w) 0 Это условие не может выполняться, т.к. по нашим предположениям, индивид является рискофобом: v”(.) < 0 v’(.) - монотонно убывающая функция, ее значения могут быть одинаковы только тогда, когда одинаковы аргументы! Наконец, рассмотрим условие (3): pv '( w L x px )(1 p ) (1 p )v '( w px ) p 0, x L p(1 p ) v '( w pL) v '( w pL) 0 v '( w pL) v '( w pL) Именно оно и характеризует решение задачи этого индивида. Мы приходим к важному выводу: при актуарно справедливой страховке, рискофоб всегда страхуется на полную стоимость ущерба! Контингентные блага Для описания выбора в условиях неопределенности иногда бывает удобно переопределить понятие блага: - Пусть S – мн-во состояний мира - ps – объективная вероятность состояния мира s S Будем называть контингентным благом xis право на получение x единиц i-того физического блага в состоянии мира s. Реальный пример контингентного блага – фьючерсный контракт. Эта конструкция оказывается очень полезной при формулировке, например, моделей общего равновесия в экономике с неопределенностью. Но помимо этого, она также позволяет создавать красивые и удобные иллюстрации для более простых моделей – например, модели спроса на страховку Модель спроса на страховку в терминах контингентных благ Вернемся к модели спроса на страховку. В ней фигурирует только одно физическое благо – деньги или богатство, и имеется два состояния мира: L: страховой случай наступает (вероятность: p) NL: страховой случай не наступает (вероятность: 1 – p) Таким образом, можно задать два контингентных блага: xL: богатство в состоянии мира L xNL: богатство в состоянии мира NL Предположительно, вначале агент не имеет никакой страховки, поэтому его богатство составляет w – L рублей, если страховой случай наступает, и w, если он не наступает. Таким образом, его первоначальный запас контингентных благ: (w – L, w) Выведем уравнение бюджетной линии в терминах контингентных благ: Как и прежде, обозначим объем приобретаемой индивидом страховки за x. Тогда богатство индивида в состояниях мира L и NL описывается следующей системой уравнений: XL w L x x X NL w x 0 x L Эта система задает уравнение бюджетной линии параметрически; XL, и XNL выражены через переменную x. Чтобы получить собственно уравнение бюджетной линии в терминах контингентных благ, выразим x, например, из 1 1 второго уравнения системы XL X NL w L и подставим в первое. После некоторых преобразований, мы получим: w L X L w L; w L X NL w; w; А вот графическая иллюстрация бюджетного ограничения в модели спроса на страховку в терминах контингентных благ. 1) Пунктирная 45º линия – это т.н. «безрисковая линия». В любом наборе, принадлежащем ей, индивид обладает одинаковым богатством в каждом состоянии мира. 2) Зеленый отрезок – это бюджетная линия. Он ограничен двумя точками: XNL Точка ω (первоначальный набор контингентных благ, (w – L, w)) соответствует минимальному (x = 0) объему страхового покрытия. бюджетная линия ω w Точка на безрисковой линии (w – γL, w – γL) соответствует максимально возможному (x = L) объему страхового покрытия. w –γL «безрисковая линия» 0 w–L w – γL XL Между двумя этими точками расположены те наборы контингентных благ, которые достигаются при 0 < x < L. Теперь давайте перейдем к иллюстрации предпочтений в пространстве контингентных благ. NB! В наших иллюстрациях мы будем опираться на т.н. обобщенную функцию ожидаемой полезности, в которой элементарная ф-ция полезности v(.) может зависеть от состояния мира. Вначале, рассмотрим несколько простых, но довольно радикальных примеров: Пример 1: Индивид заботится XNL только о своем богатстве в состоянии мира L. Такая предпосылка реалистична для тех, кто склонен сильно переоценивать вероятность несчастных случаев. Этим людям неважно, каким будет их богатство, если несчастного случая не будет – ведь они уверены, что беда обязательно случится! 0 XL Пример 2: Индивид заботится только о своем богатстве в состоянии мира NL. Эта предпосылка характеризовала бы чрезвычайно беспечных людей, сильно недооценивающих вероятность несчастных случаев. Этим людям неважно, каким будет их богатство, если несчастный случай все-таки произойдет: каждый из них уверен, что «уж со мнойто такого точно не случится!» XNL 0 XL Пример 3: Герой этого примера – индивид, нейтральный к риску. Его обобщенная функция ожидаемой полезности имеет вид: U(.) = pLvL(xL) + (1 – pL)vNL(xNL) где vL(xL) = aL + bLxL и vNL(xNL) = aNL + bNLxNL Предельная норма замещения блага контингентного блага xL контингентным благом xNL для такого агента постоянна и отрицательна: MRSxL x NL pLbL (1 pL )bNL XNL Кривые безразличия функции ожидаемой полезности этих людей представляют собой прямые линии. 0 XL Пример 4: Рассмотрим радикальную форму рискофобии, когда индивид заботится только о той сумме, которую он получит гарантированно (независимо от состояния мира), а в возможность случайно выиграть что-то сверх нее он просто не верит. Кривые безразличия для функции ожидаемой полезности такого агента были бы сходны с таковыми для Леонтьевской функции: XNL 0 безрисковая линия XL Пример 5: Рассмотрим классического рискофоба, чья элементарная функция полезности строго вогнута и не зависит от состояния мира. Его функция ожидаемой полезности имеет вид: U(.) = pLv(xL) + (1 – pL)v(xNL) где v’(.) > 0, v”(.) < 0 Модуль предельной нормы замещения контингентного блага xL контингентным благом xNL непрерывно убывает XNL по xL (и непрерывно возрастает по xN): MRSxL xNL pL v '( xL ) (1 pL )v '( xNL ) Кривые безразличия функции ожидаемой полезности для него строго выпуклы. 0 XL Пример 6: Рассмотрим классического рискофила, чья элементарная функция полезности строго выпукла и не зависит от состояния мира. Рассуждая аналогично предыдущему случаю, можно показать, что кривые безразличия его функции ожидаемой полезности строго вогнуты: XNL 0 XL Вернемся к нашей модели, и проиллюстрируем рассмотренный ранее пример со спросом рискофоба на актуарно справедливую страховку: XNL XL = XNL, “certainty line” U pv( X L ) (1 p)v( X NL ) w w tg 1 w – γL XL 0 w–L w – γL α 1 X NL w L 1 w XL Графическая иллюстрация решения задачи страхователя является очень удобным инструментом для быстрого ответа на качественные вопросы, касающиеся сравнительной статики, например: как меняется спрос на страховку с изменением вероятности несчастного случая? с изменением цены страховки? с изменением отношения к риску, и т.д. Но при необходимости (если ответ не очевиден сразу, или решение внутреннее и нам необходим точный ответ) мы могли бы сформулировать и решить задачу страхователя в терминах контингентных благ аналитически: max pv ( X L ) (1 p )v( X NL ) X L , X NL 1 1 XL X NL w L w; w L X L w L; w L X NL w; Решать ее «в лоб» довольно тяжело: к счастью, при монотонных предпочтениях и некоторых предпосылках о v(.) для каждого из трех типов страхователей (рискофоб, рискофил, риск-нейтрал) есть лишь три типа решений: Для рискофоба существует всего три возможных типа решений: Тип 1: Ущерб не страхуется. Это решение имеет место, если тангенс угла наклона бюджетной линии превышает тангенс угла наклона кривой безразличия в точке (w – L, w): X * w L L X NL * w pv '( w L) 1 (1 p )v '( w) XNL w w –γL 0 w–L w – γL XL Тип 2: Ущерб страхуется частично (внутреннее решение). Это решение находится из уравнения бюджетной линии и условия касания кривой безразличия и бюджетной линии. При этом нужно иметь в виду, что решение должно лежать правее точки первоначального запаса, и левее точки полной застрахованности: pv '( X L ) 1 (1 p )v '( X ) NL 1 1 X L X NL w L w w L X L w L w L X NL w XNL w w –γL 0 w–L w – γL XL Тип 3: Ущерб страхуется полностью. Это решение имеет место, если тангенс угла наклона бюджетной линии меньше тангенса угла наклона кривой безразличия в точке полной застрахованности, (w – γL, w – γL): X w L L X NL w L p 1 p 1 XNL w w –γL 0 w–L w – γL XL А каковы возможные типы решения задачи страхователя-рискофила? Рискнейтрала? Отношение к риску: CE(L) и RP(L) в пространстве контингентных благ Набор контингентных благ, соответствующий лотерее L XA X’A 1) Лотерея L в состоянии мира А приносит Х’A рублей, в состоянии мира B – Х’B рублей. 2) Розовые линии – кривые безразличия для функции ожидаемой полезности «Безрисковый» набор, эквивалентный E(L) E(L) «Безрисковый» набор, эквивалентный лотерее L RP(L) CE(L) 0 X’B XB 3) Синяя линия – множество лотерей с таким же ожидаемым выигрышем, как у L. Она же – кривая безразличия риск-нейтрала.