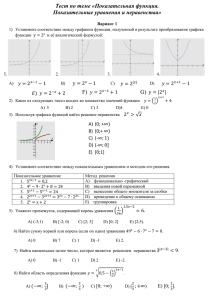
x(2)

КАК РЕШИТЬ ЗАДАЧУ НА
НАХОЖДЕНИЕ МАКСИМАЛЬНОГО
И МИНИМАЛЬНОГО ЗНАЧЕНИЯ
ФУНКЦИИ
Графический способ
решения
РАССМОТРИМ ЗАДАЧУ НА ПРИМЕРЕ
КОТОРОЙ ПОКАЖЕМ РЕШЕНИЕ
ЗАДАЧ НА НАХОЖДЕНИЕ
М А К С И М А Л Ь Н О Г О
И
МИНИМАЛЬНОГО ЗНАЧЕНИЯ
Ф
У
Н
К
Ц
И
И
УСЛОВИЕ ЗАДАЧИ
Найти максимальное и минимальное
значение функции f(x)=2x(1)-x(2)
при условиях
2x(1)–x(2)<=12,
x(1)–x(2)<=6,
x(1)–3x(2)>=1,
x(1)>=0,
x(2)>=0;
ШАГ 1
Построим графики уравнений
2x(1)-x(2)=12
x(1)-x(2)=6
x(1)-3x(2)=1
x(1)=0
x(2)=0
ПОСТРОИМ ГРАФИК УРАВНЕНИЯ
2x(1)-x(2)=12 (I)
1.
Графиком данного
уравнения
является прямая
Для построения
графика
необходимо взять
только две точки
2. Составим таблицу
значений
3. Построим график
уравнения
ПОСТРОИМ ГРАФИК УРАВНЕНИЯ
x(1)-x(2)=6 (II)
1.
Графиком данного
уравнения
является прямая
Для построения
графика
необходимо взять
только две точки
2. Составим таблицу
значений
3. Построим график
уравнения
ПОСТРОИМ ГРАФИК УРАВНЕНИЯ
x(1)-3x(2)=1 (III)
1.
Графиком данного
уравнения
является прямая
Для построения
графика
необходимо взять
только две точки
2. Составим таблицу
значений
3. Построим график
уравнения
ПОСТРОИМ ГРАФИК УРАВНЕНИЯ
x(1)=0 (IV)
1.
Графиком данного
уравнения
является прямая,
которая проходит
по оси ОX(2)
2. Построим график
уравнения
ПОСТРОИМ ГРАФИК УРАВНЕНИЯ
x(2)=0 (V)
1.
Графиком данного
уравнения
является прямая,
которая проходит
по оси ОX(1)
2. Построим график
уравнения
Построили графики уравнений
2x(1)-x(2)=12 (I)
x(1)-x(2)=6 (II)
x(1)-3x(2)=1 (III)
x(1)=0 (IV)
x(2)=0 (V)
ШАГ 2
Найдем решение системы неравенств
2x(1)–x(2)<=12,
x(1)–x(2)<=6,
x(1)–3x(2)>=1,
x(1)>=0,
x(2)>=0;
Найдем решение неравенства
2x(1)-x(2)<=12 (I)
Подставим в
неравенство координаты
х(1)=0, х(2)=0
2*0-0<=12,
0<=12 – верно
Решением неравенства
является любая пара
чисел по левую сторону
от прямой.
Найдем решение неравенства
x(1)-x(2)<=6 (II)
Подставим в
неравенство координаты
х(1)=0, х(2)=0
0-0<=6,
0<=6 – верно
Решением неравенства
является любая пара
чисел по левую сторону
от прямой.
Найдем решение неравенства
x(1)-3x(2)>=1 (III)
Подставим в
неравенство координаты
х(1)=0, х(2)=0
0-3*0>=1,
0>=1 – неверно
Решением неравенства
является любая пара
чисел по правую сторону
от прямой.
Найдем решение неравенства
x(1)>=0 (IV)
Подставим в
неравенство
координаты х(1)=1
1>=1 – верно
Решением неравенства
является любая пара
чисел по правую
сторону от прямой.
Найдем решение неравенства
x(2)>=0 (V)
Подставим в
неравенство
координаты х(2)=1
1>=1 – верно
Решением
неравенства является
любая пара чисел по
верхнюю сторону от
прямой.
Нашли решение системы
неравенств
Треугольник АВС – многоугольник решений
Найдем МАХ и МIN целевой функции
f(x)=2x(1)+x(2)
Строим вектор N с
координатами х(1)=2,
х(2)=1
Вектор N – это вектор
наибольшего
возрастания целевой
функции
Построим линию уровня
перпендикулярную
вектору N
Передвигаем
линию уровня по
направлению
вектора N до
пересечения с
самой дальней
точкой
многоугольника
решений. Этой
точкой является
точка В с
координатами (7;2)
Передвигаем
линию уровня
против направления
вектора N до
пересечения с
самой дальней
точкой
многоугольника
решений. Этой
точкой является
точка А – это точка
МIN. Координаты
точки (1;0)
Вычислим MAX и MIN функции
f MAX=2*В(х(1)-В(х2)
f MAX=2*7-2=12
f MIN=2*А(х(1)-А(х(2)
f MIN=2*1-0=2
Максимум функции равен 12
f MAX=12
Минимум функции равен 2
f MIN=2