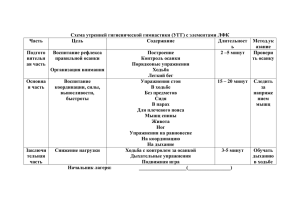
Организация самостоятельной деятельности на уроках
реклама

Самостоятельная учебная деятельность и её виды Цели: повышать эффективность учебно-воспитательного процесса и качество знаний обучающихся; глубже развивать их творческое мышление; научить учиться с помощью организации самостоятельной деятельности; Задачи: предоставить каждому обучающемуся право искать себя в рамках урока, на занятиях факультатива, на занятиях по индивидуальным планам, включаясь в самостоятельные, познавательные исследования; формировать положительную мотивацию к изучению математики; создать условия для самообразования обучающихся; заинтересовать исследованиями при решении различных увлекательных задач; задания на уроках приблизить к занимательным, неожиданным, удивительным, которые вызывают интерес у обучающихся к учебному предмету Уровни самостоятельной деятельности действия обучающихся по заданному образцу; репродуктивная деятельность по воспроизведению информации о различных свойствах изучаемого объекта; деятельность самостоятельного применения приобретённых знаний; самостоятельная деятельность по переносу знаний в новых ситуациях Требования к организации самостоятельной деятельности: порядок и приёмы выполнения работы; соответствие учебных возможностей; сочетание разнообразных видов работ; развитие познавательных способностей и инициативы, творческого мышления; выработка навыков и привычки к труду Формы организации самостоятельной работы: • индивидуальные • фронтальные •групповые Типы самостоятельной работы: • воспроизводящие; • реконструктивно-вариативные; • эвристические; • творческие Виды самостоятельной работы: работа с книгой упражнения практические и лабораторные работы контрольные работы, диктанты, сочинения доклады и рефераты выполнение заданий в связи с экскурсиями и наблюдениями в природе домашние лабораторные опыты и наблюдения техническое моделирование и конструирование Система упражнений. По целевому назначению упражнения можно разделить на три группы: •упражнения для изучения материала, приобретение умений и навыков •упражнения для закрепления пройденного материала •контрольные задания с целью проверки глубины полученных знаний Этапы Анализ содержания Цели План Реализация плана Проверка правильности действий Другие варианты действий Сопоставление с первым вариантом Устные упражнения. По горизонтали: 1. Геометрическая фигура 1 6 2 3 4 5 2. Символ, с помощью которого обозначают натуральные числа. 3. Инструмент для проведения отрезков. 4. Результат сложения. 5. Результат деления. По вертикали: 6. Знак одного из действий. Устные упражнения. Решите анаграммы: ДВАКАТР, РОЗТЕКО, ТЕРГАК и объясните, что означает каждое слово. Ответ: квадрат, отрезок, гектар. Устные упражнения. Раза два в неделю детям дают наборы из пяти «столбиков». Каждый ученик в «уме» выполняет все действия, затем на бумаге записывает только окончательные ответы и этот лист сдаёт на проверку. а) 50 б) 20 в) 40 г) 0 д) 53 Работа с учебником: • работу тщательно планировать • управлять действиями обучающимися • сочетать с другими видами работ • нельзя заучивать прочитанное наизусть • использовать графический материал • целенаправленнее работать с вопросами, которые даются в конце параграфа Изучение нового материала. 1. 2. 3. 4. 5. Прочитайте 1 абзац. О чём в нём говорится? Как его озаглавили? Почему фигуру назвали луч. Прочитайте 2 абзац. О чём в нём говорится? Как его можно озаглавить? Что обозначает в учебнике вертикальная черта? (Сведения, на которые следует обратить внимание). Прочитайте 3 абзац и рассмотрите рисунок. Сейчас вы попробуете выучить это определение и рассказать друг другу. Закрепление: На сколько частей делят плоскость две пересекающиеся прямые? 2. Какие фигуры начерчены на доске? 1. А В А А В Как называются точки А и В? Можно ли измерить длину прямой? Луча? Как правильно обозначить луч? 3. Какое определение мы выучили на уроке? Сформулируйте его. В Работа по плану План доказательства признаков равенства треугольников 1. Сроим третий треугольник, равный первому и определённым образом расположенный относительно второго. 2. Доказываем, что третий треугольник совпадает со вторым. 3. Делаем вывод: если первый и третий треугольники равны, и третий совпадает со вторым, значит, первый и второй треугольники равны План решения задач Найти расстояние между точками А и В ,если а) А (3; 0) и В (0; 4) б) А (4; 2) и В (1; 6) 1.Постройте точки А и В по их координатам 2.Определите вид треугольника АОВ 3. Сформулируйте теорему, которую можно использовать для вычисления отрезка АВ. Найдите АВ. 4. Запишите в общем виде формулу для вычисления длины отрезка АВ, если А (х; 0); В (0; у) Y В (0; 4) 0 А (3; 0) х Связь между старым и новым • Просмотрите в учебнике доказательство второго признака равенства треугольников. • Составьте план доказательства. • Сравните его с планом доказательства первого признака; отметьте, в чем разница, сделайте выводы. При изучении темы «Уравнение прямой» предлагается повторить материал о линейной функции и ответить на вопросы: что является графиком линейной функции? Приведите пример и постройте график. сколько пар соответствующих значений Х и У надо задать , чтобы построить график? Каково взаимное расположение графиков? у = 0,5х+3; у = 0,5х у = 0,5х -1 У = кх + в1; у = кх +в2 Самоконтроль. 1.Дать рецензию на ответ товарища. 2.Найти ошибку 1305 : 0,45 = 13050 :45 = 290 1470 : 1,4 = 14700 : 14 = 1050 у 3.С помощью теоремы Виета проверьте, являются ли корнями уравнения 2х2 – 3х + 1 = 0 числа 0,5 и 1 Верны ли следующие высказывания: Y < 0, х = 1 Y >0, х = 4 Y < 0, х = 1,5 Y > 0, х = - 3 4. 3 1 3 х Практическая работа Уго л 100 200 300 400 500 600 700 800 6 8 7 6 5 4 3 1 1 3 4 5 6 7 8 6 Итог урока Скорость Время 18 км/ч 3 ч. 90 км/ч Расстояни е 450 км 20 ч. 600 км Длина: а 3 дм Ширина: в 4 дм Площадь: S Периметр: Р 16 см 5 см 20 дм 64 см 80 дм 24 см Итог урока Найдите и запишите два отрезка, две прямые и три луча. 1. D E A N B F C K 2. Начертите луч CD. Постройте луч, дополнительный лучу CD и обозначьте его. На каждом луче отложите от его начала отрезок длиной 3 см 4 мм. 3. Начертите прямую МК, луч NP и отрезки АВ и CD так, чтобы прямая МК пересекала отрезки АВ и CD. Поменяться тетрадями и сверить с доской.