28.05.14 Задачи на построение

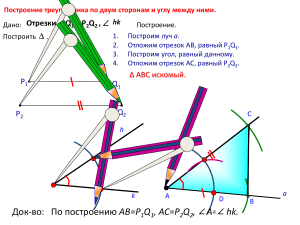
Задачи на построение
Это такие задачи, при
решении которых
нужно построить
геометрическую
фигуру,
удовлетворяющую
условию задачи с
помощью циркуля и
линейки без делений.
Схема решения задач на построение
1. Анализ (рисунок искомой фигуры,
устанавливающий связи между данными
задачи и искомыми элементами; и план
построения).
2. Построение по намеченному плану.
3. Доказательство, что данная фигура
удовлетворяет условиям задачи.
4. Исследование( при любых ли данных задача
имеет решение, и если имеет, то сколько).
В 7 классе мы с вами решаем самые простые
задачи на построение, поэтому иногда достаточно
только второго пункта схемы( или второго и
Из истории математики
В 1672 г. Датский математик Георг Мор, а затем в
1797 г. итальянский учёный Лоренцо Маскерони
доказали независимо один от другого такое
утверждение: всякая задача на построение,
разрешимая с помощью циркуля и линейки,
разрешима также с помощью одного только
циркуля. Эти название построения носят
построения Мора - Маскерони.
Швейцарский геометр Якоб Штейнер в 1883 г., а
несколько раньше французский математик
Ж.Понселе доказали тоже независимо друг
от друга такое утверждение: любая задача
на построение, разрешимая с помощью
циркуля и линейки, может быть разрешена с
помощью линейки, если только в плоскости
чертежа задана окружность и её центр. Такие
построения носят название построения
Понселе -Штейнера.
Построение треугольника по трем сторонам.
Дано:
отрезки
Р1Q1, Р2Q2, P3Q3.
P1
Q1
P2
P3
1. Построим луч а.
2. Отложим отрезок АВ, равный P1Q1.
3. Построим дугу с центром в т. А и
радиусом Р2Q2.
4. Построим дугу с центром в т.В и
радиусом P3Q3.
Q2
С
Q3
А
а
В
Треугольник АВС искомый. Обоснуй, используя III признак.
Построение треугольника по двум
сторонам и углу между ними.
1. Построим луч а.
Дано:
2. Отложим отрезок АВ, равный P1Q1.
3. Построим угол, равный данному.
Отрезки Р1Q1 и Р2Q2
4. Отложим отрезок АС, равный P2Q2.
P1
P2
Q1
Q2
С
h
Угол hk
а
А
D
В
Треугольник АВС искомый. Обоснуй, используя I признак.
k
Построение треугольника по стороне и
двум прилежащим к ней углам.
1. Построим луч а.
Дано:
2. Отложим отрезок АВ, равный P1Q1.
3. Построим угол, равный данному h1k1.
Отрезок Р1Q1
4. Построим угол, равный h2k2 .
P1
С
Q1
h1
h2
k1
а
А
N
D
В
Треугольник АВС искомый. Обоснуй, используя II признак.
Угол h1k1
k2
Спасибо
за урок