Математический анализ 1 семестр Исследование функций. Построение графиков.

Дистанционный курс высшей математики
НИЯУ МИФИ
Математический анализ
1 семестр
Лекция 12
Исследование функций.
Построение графиков.
Длина кривой.
4 декабря 2014 года
Лектор: Профессор НИЯУ МИФИ, д.ф.-м.н.
Орловский Дмитрий Германович
Исследование стационарной точки
Пусть функция f(x) дифференцируема в интервале (a–δ;a+δ) и
существует f’’(a). Пусть также f’(a)=0, а f’’(a)≠0.
Если f’’(a)<0, то x=a является точкой строгого максимума f(x).
Если f’’(a)>0, то x=a является точкой строгого минимума f(x).
1
f ' ' (a)( x  a) 2   ( x)( x  a) 2
2
1
f ( x)  f (a )  [ f ' ' (a )   ( x)]( x  a ) 2
2
f ( x)  f (a)  f ' (a)( x  a) 
1
1
lim [ f ' ' (a)   ( x)]  f ' ' (a)  0
x a 2
2
В некоторой окрестности (a–δ1;a+δ1) точки x=a
Sign ( f ( x)  f (a))  Sign f ' ' (a)
Исследование стационарной точки
Пусть функция f(x) имеет n-1 производную в интервале (a-(a–δ;a+δ) и существует f(n)(a). Пусть также
f ' (a)  f ' ' (a)  . . .  f ( n1) (a)  0, f ( n) (a)  0.
Тогда если
(1) n=2k+1 x=a не является точкой экстремума
(2) n=2k f(n)(a)<0 x=a является точкой максимума
f(n)(a)>0 x=a является точкой минимума
f ( k ) (a)
f ( n ) (a)
k
f ( x)  f (a)  f ' (a)( x  a)  ... 
( x  a)  ... 
( x  a) n  rn ( x),
k!
n!
rn ( x)  o(( x  a) n )   ( x)( x  a) n
(lim  ( x)  0).
xa
Исследование стационарной точки
f ( n ) (a)
f ( x)  f (a) 
( x  a) n   ( x)( x  a) n ,
n!
f ( n ) (a)
f ( x)  f (a )  (
  ( x))( x  a) n .
n!
f ( n ) (a)
f ( n ) (a)
lim (
  ( x)) 
 0.
x a
n!
n!
В некоторой окрестности (a–δ1;a+δ1) точки x=a
Sign ( f ( x)  f (a))  Sign ( f ( n ) (a)( x  a) n ).
Выпуклость функции
Функция называется выпуклой вниз (выпуклой) в интервале (a;b),
если для любой точки x0∊(a;b) и всех x∊(a;b)
f ( x)  f ( x0 )  f ' ( x0 )( x  x0 ).
Функция называется выпуклой вверх (вогнутой) в интервале (a;b),
если для любой точки x0∊(a;b) и всех x∊(a;b)
f ( x)  f ( x0 )  f ' ( x0 )( x  x0 ).
Выпуклость функции
Дифференцируемая в интервале (a;b) функция f(x) выпукла
тогда и только тогда ее производная возрастает.
(1) Функция выпукла и x1<x2
f ( x)  f ( x1 )  f ' ( x1 )( x  x1 ),
f ( x2 )  f ( x1 )  f ' ( x1 )( x2  x1 ),
f ' ( x1 ) 
f ( x2 )  f ( x1 )
,
x2  x1
f ( x)  f ( x2 )  f ' ( x2 )( x  x2 )
f ( x1 )  f ( x2 )  f ' ( x2 )( x1  x2 )
f ( x2 )  f ( x1 )
 f ' ( x2 )
x2  x1
f ' ( x1 )  f ' ( x2 ).
Выпуклость функции
Дифференцируемая в интервале (a;b) функция f(x) выпукла
тогда и только тогда ее производная возрастает.
(2) Производная функция возрастает. По теореме Лагранжа
f ( x)  f ( x0 )  f ' (ξ)( x  x0 )
а) x  x0  ξ  x0  f ' (ξ)  f ' ( x0 )
f ( x)  f ( x0 )  f ' (ξ )( x  x0 )  f ' ( x0 )( x  x0 )
f ( x)  f ( x0 )  f ' ( x0 )( x  x0 )
б) x  x0  ξ  x0  f ' (ξ)  f ' ( x0 )
f ( x)  f ( x0 )  f ' (ξ )( x  x0 )  f ' ( x0 )( x  x0 )
f ( x)  f ( x0 )  f ' ( x0 )( x  x0 )
в) x  x0 , неравенство
f ( x)  f ( x0 )  f ' ( x0 )( x  x0 )
превращается в равенство.
Выпуклость функции
Дифференцируемая в интервале (a;b) функция f(x) вогнута
тогда и только тогда ее производная убывает.
Функция f(x) вогнута тогда и только тогда, когда
g ( x)   f ( x)
выпукла, т.е. g’(x) возрастает. Однако, это равносильно тому, что
функция f’(x) = – g’(x) убывает
Выпуклость функции
Дважды дифференцируемая в интервале (a;b) функция f(x)
выпукла тогда и только тогда, когда всюду f’’(x)≥0.
(1)
f ' ' ( x )  0.
f ' ' (ξ )
f ( x)  f ( x0 )  f ' ( x0 )( x  x0 ) 
( x  x0 ) 2  f ( x0 )  f ' ( x0 )( x  x0 ).
2
(2) Функция выпукла.
f ' ' ( x0 )
( x  x0 ) 2   ( x)( x  x0 ) 2 (lim  ( x)  0).
xa
2
f ( x)  ( f ( x0 )  f ' ( x0 )( x  x0 ))
f ' ' ( x0 )  2
 2 ( x)  2 ( x)
2
( x  x0 )
f ( x)  f ( x0 )  f ' ( x0 )( x  x0 ) 
f ' ' ( x0 )  2 lim  ( x)  0.
xa
Выпуклость функции
Дважды дифференцируемая в интервале (a;b) функция f(x)
вогнута тогда и только тогда, когда всюду f’’(x)≤0.
(1) f ' ' ( x )  0.
f ' ' (ξ )
f ( x)  f ( x0 )  f ' ( x0 )( x  x0 ) 
( x  x0 ) 2  f ( x0 )  f ' ( x0 )( x  x0 ).
2
(2) Функция вогнута.
f ' ' ( x0 )
( x  x0 ) 2   ( x)( x  x0 ) 2 (lim  ( x)  0).
xa
2
f ( x)  ( f ( x0 )  f ' ( x0 )( x  x0 ))
f ' ' ( x0 )  2
 2 ( x)  2 ( x)
2
( x  x0 )
f ( x)  f ( x0 )  f ' ( x0 )( x  x0 ) 
f ' ' ( x0 )  2 lim  ( x)  0.
xa
Точка перегиба
Точка x=a называется точкой перегиба функции f(x) если
существует такое δ>0, что в интервалах (a–δ;a) и (a;a+δ) эта
функция выпукла в разные стороны.
Это определение равносильно тому, что производная либо
меняет возрастание на убывание, либо меняет убывание на
возрастание.
Точка перегиба
Необходимое условие точки перегиба.
Пусть точка x=a является точкой перегиба функции f(x) и в этой
точке у нее существует вторая производная. Тогда
f ' ' (a )  0.
Опасные моменты!
Равенство нулю второй производной является необходимым
условием наличия перегиба. Однако, достаточным условием
оно не является.
Точка перегиба
y  x4
y'  4 x3
y' '  4 x 2  0
Данная функция выпукла в одну сторону на всей числовой прямой
и перегибов не имеет. Тем не менее ее вторая производная в нуле
равна нулю.
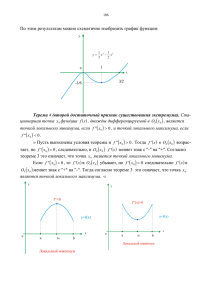
Точка перегиба
Перегиб
Нет перегиба
Перегиб
Нет перегиба
Точка перегиба
Пусть функция f(x) имеет n-1 производную в интервале (a-(a–δ;a+ δ) и существует f(n)(a). Пусть также
f ' ' (a)  . . .  f ( n1) (a)  0, f ( n ) (a)  0.
Тогда если
(1) n=2k+1 x=a является точкой перегиба
(2) n=2k
x=a не является точкой перегиба
Пример:
f ( x)  x 4 , a  0.
f ' ' ( x)  12 x 2 , f ' ' ' ( x)  24 x, f ( IV) ( x)  24.
f ' ' (0)  0, f ' ' ' (0)  0, f ( IV) (0)  0.
n=4, x=0 не является точкой перегиба.
Асимптоты
Вертикальная асимптота
Прямая x=a называется асимптотой если
lim f ( x)  .
x a
Асимптота может быть односторонней:
lim f ( x)   (левая односторонняя асимптота)
xa 0
lim f ( x)   (правая односторонняя асимптота)
xa  0
Асимптоты
y
1
x 1
асимптота
y  sin( 1 / x)
нет асимптоты
y  ln x
асимптота
y  e1/ x
асимптота
y
нет асимптоты
1
1
sin
x
x
Асимптоты
Наклонная асимптота
Наклонной асимптотой графика функции y=f(x) при x→+∞
называется прямая y=kx+b, если выполнены два условия:
(1) некоторый луч (a;+∞) целиком содержится в области
определения функции;
(2) расстояние по вертикали между графиком и прямой
стремится к 0 при x→+∞ :
lim [ f ( x)  (kx  b)]  0.
x  
Наклонной асимптотой графика функции y=f(x) при x→–∞
называется прямая y=kx+b, если выполнены два условия:
(1) некоторый луч (–∞;a) целиком содержится в области
определения функции;
(2) расстояние по вертикали между графиком и прямой
стремится к 0 при x→–∞ :
lim [ f ( x)  (kx  b)]  0.
x  
Асимптоты
Принято выделять частный случай наклонной асимптоты при k=0.
Такая асимптота называется горизонтальной. Прямая y=b является
горизонтальной асимптотой при x→+∞ ( x→–∞ ) если
lim f ( x)  b ( lim f ( x)  b).
x  
x  
Асимптоты
Нахождение наклонной асимптоты
Прямая y=kx+b является асимптотой функции f(x) при x→+∞ тогда
и только тогда, когда
f ( x)
k  lim
, b  lim ( f ( x)  kx).
x  
x  
x
Прямая y=kx+b является асимптотой функции f(x) при x→–∞ тогда и
только тогда, когда
f ( x)
k  lim
, b  lim ( f ( x)  kx).
x  
x  
x
Асимптоты
Пусть прямая y=kx+b является асимптотой при x→±∞. Тогда
lim [ f ( x)  (kx  b)]  0
x  
lim
x  
f ( x)
f ( x)
b
f ( x)  (kx  b)
 k  lim (
 k  )  k  lim
 k 0 k
x


x


x
x
x
x
lim ( f ( x)  kx)  b  lim [ f ( x)  (kx  b)]  b  0  b
x  
x  
Обратно, пусть выполнены предельные соотношения, тогда
lim [ f ( x)  (kx  b)]  lim ( f ( x)  kx)  b  b  b  0
x  
x  
Примеры
Построить график функции
( x  1)3
y
( x  1) 2
3( x  1) 2 ( x  1) 2  ( x  1)3 2( x  1) ( x  1) 2 (3x  3  2 x  2) ( x  1) 2 ( x  5)
y' 


4
3
( x  1)
( x  1)
( x  1)3
x 3  3x 2  9 x  5
(3x 2  6 x  9)( x  1)3  ( x 3  3x 2  9 x  5)3( x  1) 2
y' '  [
]' 

3
6
( x  1)
( x  1)
(3x 3  6 x 2  9 x  3x 2  6 x  9)  (3x 3  9 x 2  27 x  15) 24( x  1)


4
( x  1)
( x  1) 4
Примеры
Нахождение асимптот:
Вертикальная x=1.
Наклонная y=kx+b.
y ( x)
( x  1)3
k  lim
 lim
1
2
x 
x


x
x( x  1)
( x  1)3
( x  1) 3  x( x  1) 2
b  lim ( y ( x)  kx)  lim (
 x)  lim

2
x 
x  ( x  1) 2
x 
( x  1)
( x 3  3x 2  3x  1)  ( x 3  2 x 2  x)
 5x 2  2 x  1
 lim
 lim
 5
2
2
x 
x


( x  1)
( x  1)
y  x 5
Примеры
Знаки функции и производных
Точка экстремума
x  5; y  13,5
Точка перегиба
x  1; y  0
Примеры
График
( x  1)3
y
( x  1) 2
Длина кривой
Пусть на отрезке [α;β] заданы три функции f1(t), f2(t), f3(t). Множество
точек
L  {( x; y; z ) : x  f1 (t ), y  f 2 (t ), z  f 3 (t ),   t   }
называется параметрической кривой. Точка A(f1(α);f2(α);f3(α)) на кривой
L называется началом кривой, а точка B(f1(β);f2(β);f3(β)) называется
концом кривой. Часто начало и конец называются одним словом:
концы кривой.
Если функции f1(t), f2(t), f3(t) непрерывны, кривая L называется
непрерывной кривой (кривая класса C или C0).
Если функции f1(t), f2(t), f3(t) непрерывно дифференцируемы, то
кривая L называется гладкой кривой (кривая класса С1).
Длина кривой
Замечание. Часто гладкой называют
кривую при дополнительном условии
[ f1 ' (t )]2  [ f 2 ' (t )]2  [ f 3 ' (t )]2  0.
(1)
Однако, во многих утверждениях это
условие оказывается не нужным. Если
для гладкой кривой это последнее
условие выполнено, будем называть
такую кривую регулярной.
Условие (1) может быть выполнено в одних точках и не выполнено
в других точках. Точки, в которых условие (1) выполнено, назовем
регулярными, а точки, в которых это условие не выполнено, назовем
особыми точками кривой.
Длина кривой
Разбиение
T  {t0 , t1 , t2 , ... , tn }
  t0  t1  t2  ...  tn  
каждой точке разбиения отрезка отвечает точка на кривой
M i ( f1 (ti ); f 2 (ti ); f 3 (ti ))
Длину отрезка Mi-1Mi обозначим
li  ( f1 (ti )  f1 (ti 1 )) 2  ( f 2 (ti )  f 2 (ti 1 )) 2  ( f 3 (ti )  f3 (ti 1 )) 2
Длина кривой
Длину ломаной
M 0 M 1M 2 ... M n
обозначим
n
l (T )   li
i 1
Определение. Длиной кривой называется величина
| L | Sup l (T )
{T }
(кривая, у которой существует длина, называется спрямляемой).
Длина кривой
Аддитивность длины кривой
l ( AB)  l ( BC )  l ( AC )
Длина кривой
1) Пусть спрямляема кривая AC и пусть T1,T2 – произвольные
разбиения AB и BC. Тогда T= T1UT2 является разбиением AC,
причем
l (T )  l (T1 )  l (T2 ),
тогда для любого разбиения T1 кривой AB
l (T1 )  l (T )  l (T2 ) | AC | l (T2 ).
Поэтому кривая AB спрямляема и
| AB || AC | l (T2 ).
Но теперь для любого разбиения T2 кривой BC
l (T2 ) | AC |  | AB | .
Следовательно, кривая BC спрямляема и
т.е.
| BC || AC |  | AB |
| AB |  | BC || AC | .
Длина кривой
2) Пусть спрямляемы кривые AB и BC, а T – произвольное
разбиение кривой AC. Если точка B не входит в это разбиение, то
добавим ее и получим разбиение T+, которое распадается на
разбиения T1 и T2 кривых AB и BC. При этом
l (T )  l (T  )  l (T1 )  l (T2 )
Так как
l (T1 ) | AB |, l (T2 ) | BC |,
то
l (T ) | AB |  | BC | .
Отсюда следует, что кривая AC спрямляема и
| AC || AB |  | BC | .
Из пунктов 1) и 2) следует, что
| AC || AB |  | BC | .
Длина кривой
Теорема. Гладкая кривая спрямляема и ее длина удовлетворяет
неравенствам
m12  m22  m32 (   )  | L |  M12  M 22  M 32 (   ),
где
m j  Inf | f j ' (t ) |, (1  j  3),
[ ;  ]
M j  Sup | f j ' (t ) |, (1  j  3).
[ ;  ]
Длина кривой
Доказательство. Применим теорему Лагранжа
f j (ti )  f j (ti 1 )  f j ' (ξ ij )(ti  ti 1 )
m j (ti  ti 1 )  | f j (ti )  f j (ti 1 ) |  M j (ti  ti 1 )
m12  m22  m32 (ti  ti 1 )  li  M12  M 22  M 32 (ti  ti 1 )
Сложим полученные неравенства и учтем, что
n
 (t
получим
i 1
i
 ti 1 )    
m12  m22  m32 (   )  l (T )  M12  M 22  M 32 (   )
Длина кривой
m12  m22  m32 (   )  l (T )  M12  M 22  M 32 (   )
Число, стоящее справа, ограничивает множество длин всех
ломаных сверху. Поэтому рассматриваемое множество всех
этих длин имеет точную верхнюю грань (длину кривой) и по
определению точной верхней грани
| L |  M12  M 22  M 32 (   ).
Далее, по определению точной верхней грани, для любого
разбиения
но
Следовательно,
l (T ) | L |,
m12  m22  m32 (   )  l (T ).
m12  m22  m32 (   )  | L | .
Дистанционный курс высшей математики
НИЯУ МИФИ
Математический анализ.
Длина и кривизна кривой.
Лекция 12
завершена.
Спасибо за внимание!
Тема следующей лекции:
Приближенные методы решения уравнений.
Лекция состоится в четверг 11 декабря
В 10:00 по Московскому времени.