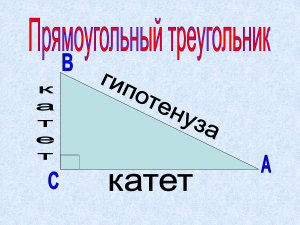
Косинусом острого угла в прямоугольном

МБОУ ООШ № 81
г. Краснодар
Тема урока:
«Синус, косинус и тангенс
острого угла прямоугольного
треугольника»
Учитель математики Дарьина Вера Сергеевна
Цели урока.
Образовательные:
формировать понятия синуса, косинуса и тангенса острого угла
прямоугольного треугольника;
Развивающие:
развивать способности к самостоятельному планированию и
организации работы; навыки коррекции собственной деятельности
через применение информационных технологий; умение обобщать,
абстрагировать и конкретизировать знания
Воспитательные:
воспитывать познавательный интерес к математике,
информационную культуру и культуру общения, самостоятельность,
способность к коллективной работе.
Математический диктант
1. Назовите стороны треугольника МРК.
2. Чему равна сумма углов треугольника?
3. Назвать стороны, противолежащие углу М.
4. Назвать стороны, прилежащие углу М.
5. Сформулировать свойство катета прямоугольного
треугольника, лежащего против угла 30°.
6. Сформулировать теорему Пифагора.
Изучение нового материала
Пусть АВС – прямоугольный
треугольник с прямым углом С и острым
углом при вершине А, равным 
В
С
А
А
АВ - гипотенуза
АС –
прилежащий
катет
В
С
ВС – противолежащий катет
Синусом острого угла в
прямоугольном треугольнике
называется отношение
противолежащего катета к
гипотенузе
В
BC
sin A =
AB
С
А
Косинусом острого угла в
прямоугольном треугольнике
называется отношение
прилежащего катета к гипотенузе
В
AC
cos A =
AB
С
А
Тангенсом острого угла в
прямоугольном треугольнике
называется отношение
противолежащего катета к
прилежащему
В
BC
tg A =
AC
С
А
Эти правила позволяют ,
зная одну из сторон
прямоугольного
треугольника и острый угол ,
находить две другие
стороны; зная две стороны,
находить острые углы
c
а


a = c sin 

b = c cos 

b
a = b tg

b = a ctg

Задача
В прямоугольном треугольнике
даны гипотенуза с и острый
угол α. Найти катеты.
Решение
C
α
A
c
B
AC = AB cos α = c cos α;
BC = AB sin α = c sin α;
III. Закрепление изученного материала
Решение прикладных задач
Найдите высоту
α=30°
S= 9м
дерева
Тень от вертикально стоящего шеста,
высота которого 33 м, составляет 3 м.
Выразите
в градусах высоту Солнца над
горизонтом.
α
Основное тригонометрическое
тождество
2
sin A
2
cos A
+
=1
tgA = sin A
cosA
Кроссворд