лек-12
реклама

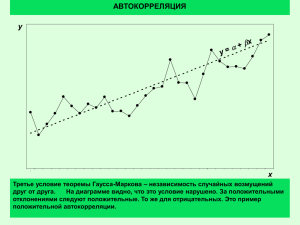
Динамические эконометрические модели Стохастические регрессоры Рассмотрим модель yt = a + bxt + et (1) Предположение: yt и xt – стационарные временные ряды, т.е. случайные величины yt имеют одно и то же распределение (аналогично и xt ). 3 случая: 1. Регрессоры xt и случайные члены et не коррелируют: Cov(xs, et) = 0 2. Значения регрессоров xt не коррелированы с et (т.е. в данный момент времени), но коррелируют с ошибками в более ранние моменты времени. Пример: 3. s, t = 1, …,n. yt = a + b1xt + b2yt-1 + et Значения регрессоров xt коррелированы с ошибками et . Теорема Пусть xt имеет конечное мат.ожидание и дисперсию. Тогда: оценки параметра b по методу наименьших квадратов являются: • в случае 1 – несмещёнными и состоятельными; • в случае 2 –состоятельными, но смещёнными; • в случае 3 – смещёнными и несостоятельными. Замечание 1. Для случая 2 в выборках большого объёма корреляция регрессора со случайным членом стремится к 0 и асимптотически есть несмещённость оценок. Замечание 2. Аналогичное утверждение верно и для множественной регрессии. Причины коррелированности: а) На случайный член и на регрессоры воздействуют одни и те же факторы; б) Ошибки при измерении регрессоров Причина а): Вместо модели yt = a + bxt + gut + nt xt = l + dut + zt рассматриваем модель yt = a + bxt + et Пример 1. В пункте А производится сырьё двух видов. Сырьё перевозится в пункт В, где на заводе производится полуфабрикат, который продаётся на завод по цене x. На заводе изготавливается конечный продукт, который перевозится в пункт С и реализуется по цене y. Цены на сырьё меняются и образуют временные ряды z1 и z2. Причина б): Пусть мы имеем искажённые, а не истинные значения x xt* = xt + ut Рассматриваем модель yt = bxt + et = b(xt* - ut) + et = bxt* + (et – but) Cov(xt*, (et – but)) = -bCov(ut, ut) 0. Опр. Динамическая эконометрическая модель – в момент времени t учитываются значения переменных как текущих, так и за предыдущие моменты времени. Опр. Лаг – константа, характеризующая величину запаздывания в воздействии фактора на результат. Опр. Лаговая переменная – факторная переменная, сдвинутая на несколько моментов времени. Типы динамических эконометрических моделей • явные модели – ARIMA (autoregressive integrated moving average) модели (метод БоксаДженкинса) – ADL (autoregressive distributed lags) модели • неявные модели • неполной корректировки • адаптивных ожиданий • рациональных ожиданий Явные модели модель авторегрессии p-го порядка AR(p) yt = b0 + b1yt-1 + b2yt-2 + … + bpyt-p + et модель скользящей средней q-го порядка MA(q) yt = et + g1et-1 + g2et-2 + … + gqet-q авторегрессионная модель скользящей средней порядков p и q соответственно ( ARMA(p,q) модель ) yt = b0 + b1yt-1 + b2yt-2 + … + bpyt-p + et + g1et-1 + g2et-2 + … + gqet-q модель с распределенным лагом p ( DL(p) ) yt = a + b0xt + b1xt-1 + … + bpxt-p + et авторегрессионная модель с распределёнными лагами порядков p и q ( ADL(p,q) модель ) yt = a + b0xt + b1xt-1 + … + bpxt-p + с1yt-1 + с2yt-2 + … + сqyt-q + et Модель с распределённым лагом (интерпретация параметров) yt a + b0 xt + b1 xt 1 + b2 xt 2 + e t b0 - краткосрочный мультипликатор b = b0 + b1 + … + bl - долгосрочный мультипликатор Преимущества и недостатки моделей ARIMA • Преимущества – – – – охватывают широкий спектр временных рядов не используются независимые переменные проверка на адекватность проста и доступна прогнозы и интервалы предсказания следуют прямо из модели • Недостатки – необходимо достаточно большое количество данных (для несезонных данных более 40 наблюдений) – при включении новых данных требуется перестройка всей модели – достаточно большие затраты времени и ресурсов Схема метода Бокса-Дженкинса • Выбор исходной модели – анализ графика временного ряда – анализ автокорреляционной функции – анализ частной автокорреляционной функции • Оценка параметров для экспериментальной проверки • Проверка адекватности модели • Использование модели для прогнозирования AR(1) Автокорреляция Частные автокорреляции 0,8 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 0 2 4 6 8 10 0 12 2 Автокорреляция 0 0,6 -0,1 0 0,4 -0,2 -0,3 0,2 -0,4 0 2 4 6 6 8 10 12 10 12 Частные автокорреляции 0,8 -0,2 0 4 8 10 12 -0,5 -0,6 -0,4 -0,7 -0,6 -0,8 -0,8 -0,9 2 4 6 8 AR(2) Частные автокорреляции Автокорреляция 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 0 0 2 4 6 8 10 2 0,8 0,8 0,6 0,6 0,4 0,4 0,2 0,2 0 -0,4 -0,6 -0,8 2 4 6 6 8 10 12 Частные автокорреляции Автокорреляция -0,2 0 4 12 8 10 12 0 -0,2 0 -0,4 -0,6 -0,8 -1 2 4 6 8 10 12 MA(1) Автокорреляция Частные автокорреляции 0 0 -0,1 0 -0,2 -0,3 -0,4 -0,5 -0,6 -0,7 -0,8 -0,9 -0,1 0 2 4 6 8 10 12 2 4 6 8 10 12 10 12 -0,2 -0,3 -0,4 -0,5 -0,6 -0,7 -0,8 -0,9 Автокорреляция Частнык автокорреляции 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 0,8 0,6 0,4 0,2 0 -0,2 0 -0,4 -0,6 0 2 4 6 8 10 12 -0,8 2 4 6 8 MA(2) Частнык автокорреляции Автокорреляция 0,8 1 0,8 0,6 0,6 0,4 0,4 0,2 0,2 0 0 -0,2 0 -0,2 0 2 4 6 8 10 12 -0,4 2 4 8 10 12 -0,4 -0,6 -0,6 -0,8 -0,8 Частные автокорреляции Автокорреляция 0 -0,1 0 -0,2 -0,3 -0,4 -0,5 -0,6 -0,7 -0,8 -0,9 6 0 -0,1 0 2 4 6 8 10 12 -0,2 -0,3 -0,4 -0,5 -0,6 -0,7 -0,8 -0,9 2 4 6 8 10 12 ARMA(1,1) Частные автокорреляции Автокорреляция 0 0 -0,1 0 2 4 6 8 10 -0,1 0 12 -0,2 -0,2 -0,3 -0,3 -0,4 -0,4 -0,5 -0,5 -0,6 -0,6 -0,7 -0,7 -0,8 -0,8 -0,9 -0,9 2 4 Автокорреляция 8 10 12 Частные автокорреляции 0,8 0,8 0,6 0,6 0,4 0,4 0,2 0,2 0 -0,2 0 6 0 2 4 6 8 10 12 -0,2 0 -0,4 -0,4 -0,6 -0,6 -0,8 -0,8 2 4 6 8 10 12 ARMA(1,1) Частные автокорреляции Автокорреляция 0,8 0,8 0,6 0,7 0,4 0,6 0,5 0,2 0,4 0 -0,2 0 2 4 6 8 10 12 0,3 0,2 -0,4 0,1 -0,6 0 0 -0,8 2 Автокорреляция 4 6 8 10 12 10 12 Частные автокорреляции 0,8 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 0 2 4 6 8 10 12 0 2 4 6 8 Модели с распределенным лагом • Конечномерная модель yt a + b0 xt + b1 xt 1 + ... + b p xt p + e t • Бесконечномерная модель yt a + b0 xt + b1 xt 1 + b2 xt 2 + ... + e t • Проблемы: – мультиколлинеарность; – уменьшение числа степеней свободы с увеличением величины лага; – автокорреляция остатков. • Структуры лага (зависимость коэффициентов bj от j): – – – – линейная геометрическая V – образная перевернутая V – образная Метод Алмон (конечномерная модель) Опр. Лаги Алмон – лаги, структура которых описывается полиномами. b j c0 + c1 j + c2 j + ... + ck j 2 k yt a + c0 ( xt + xt 1 + xt 2 + ... + xt l ) + + c1 ( xt 1 + 2 xt 2 + 3 xt 3 + ... + lxt l ) + + c2 ( xt 1 + 4 xt 2 + 9 xt 3 + ... + l xt l ) + ... + 2 + ck ( xt 1 + 2 xt 2 + 3 xt 3 + ... + l xt l ) + e t k k k • Введем новые переменные z0 xt + xt 1 + xt 2 ... + xt l z1 xt 1 + 2 xt 2 + 3xt 3 ... + lxt l z2 xt 1 + 4 xt 2 + 9 xt 3 ... + l 2 xt l …………………………………………………….. z k xt 1 + 2 k xt 2 + 3k xt 3 ... + l k xt l yt a + c0 z0 + c1 z1 + c2 z2 + ... + ck zk + e t Алгоритм метода Алмон Определяется максимальная величина лага l. Определяется степень полинома к, описывающего структуру лага. 3. Рассчитываются значения переменных z0, z1,..., zk. 4. Определяются параметры уравнения линейной регрессии. 5. Находятся параметры исходной модели с распределенным лагом. Замечания. 1. Методы определение величины лага l: - априорная информация; - измерение тесноты связи между результатом и лаговыми переменными; - критерий Шварца. 1. 2. 2. Методы определения степени полинома k - степень полинома k на единицу больше числа экстремумов в структуре лага - построение и сравнение моделей для разных значений k и выбор лучшей модели Достоинства метода Алмон: А) универсальность; Б) при k=2 или k=3 можно построить модель с лагом любой величины. В) мультиколлинеарность факторов z0,…,zk сказывается на оценках параметров b0,...,bl в меньшей степени, чем при применении стандартного МНК к исходной модели Пример. y – объем ВВП США (млрд $), x – внутренние инвестиции (млрд $). • Модель с распределенным лагом l=4 и к=2: yˆt 300 + 1,92 xt + 1,19 xt 1 + 0,81 xt 2 + 0,81 xt 3 + 1,18 xt 4 (0,21) (0,097) (0,142) (66,2) (0,21) (0,10) R 2 0,99 • Модель по стандартному МНК: yˆ t 297 + 2,08 xt + 0,78 xt 1 + 1,29 xt 2 + 0,43 xt 3 + 1,32 xt 4 (67,7) (0,31) (0,43) (0,44) R 2 0,991 (0,43) (0,097) Метод Койка для бесконечномерной модели yt a + b0 xt + b1 xt 1 + b2 xt 2 + ... + e t • Предположение: • лаг имеет геометрическую структуру: b j b0 l , 0 l 1 j yt a + b0 xt + b0 l xt 1 + b0 l2 xt 2 + ... + e t yt 1 a + b0 xt 1 + b0 l xt 2 + b0 l2 xt 3 + ... + e t 1 l yt 1 l a + b0 l xt 1 + b0 l2 xt 2 + b0 l3 xt 3 + ... + l e t 1 yt l yt 1 a l a + b0 xt + e t 1 l e t 1 Модель Койка (двухфакторная линейная авторегрессия): yt a (1 l ) + b0 xt + l yt 1 + ut ut = et – let-1. Коэффициент b0 – характеризует краткосрочное воздействие x на y. где Выражение b0/(1-l) - характеризует долгосрочное воздействие x на y. Преимущества: 1) простота метода 2) возможность анализировать и сравнивать краткосрочные и долгосрочные динамические свойства модели Проблема: одна из объясняющих переменных ( yt-1 ) коррелирует со случайным членом МНК смещённые и несостоятельные оценки по Выход: использовать нелинейный МНК для исходного уравнения. Оценивание моделей авторегрессии с распределёнными лагами yt = a + bxt + g yt-1 + et (2) yt-1 = a + bxt-1 + g yt-2 + et-1 в (2) yt = a(1+g) + bxt + bgxt-1 + g2 yt-2 + et + g et –1 yt = a/(1g) + bxt + b(gxt-1 + g2xt-2 + g3xt-3 + … ) + (et + g et –1 + g2 et –2 + … ) Модель: подставим Вывод: модель авторегрессии с распределёнными лагами (2) можно свести к модели Койка Плюс: устранена коррелированность регрессора с ошибками Минус: а) автокорреляция ошибок имеет сложную структуру б) неидентифицируемость модели Далее: применить нелинейный метод наименьших квадратов Нелинейный метод наименьших квадратов 1. 2. 3. 4. В множестве возможных значений g выбираем последовательность gh Для каждого gh вычисляем xth = xt + (gh xt-1 + gh2 xt-2 + gh3 xt-3 + … ) МНК оцениваем уравнение yt = a1 + bxth + ut Выбираем уравнение с наибольшим R2 Получаем g, a, b.