Приложение 1. Функции и графики в школьных учебниках
реклама
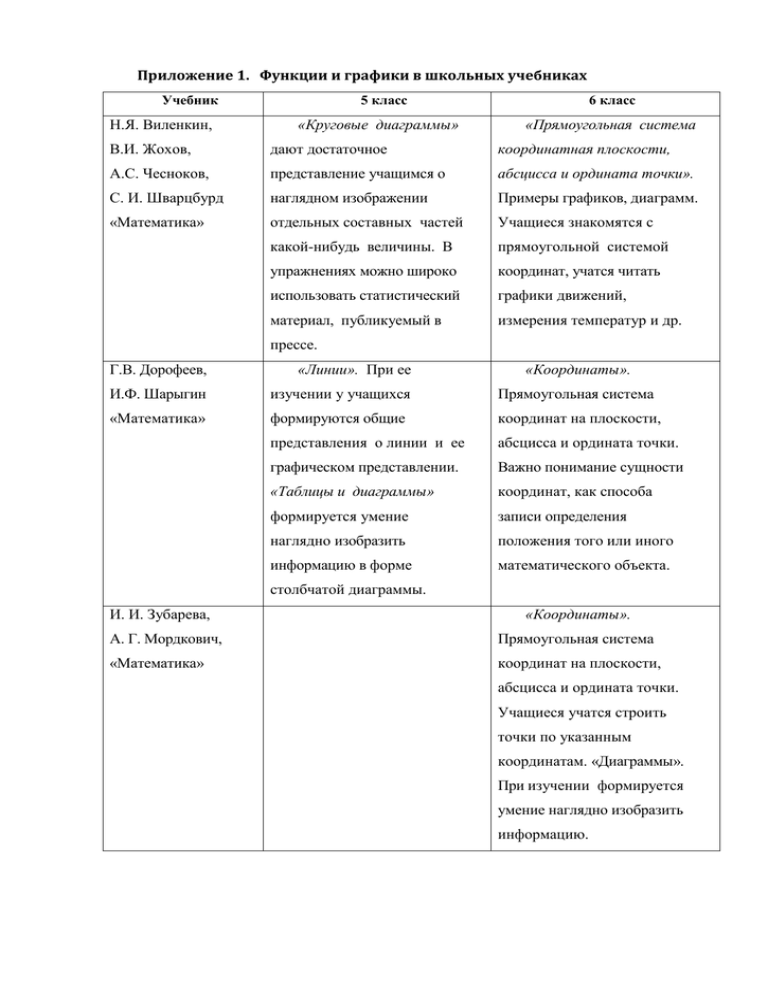
Приложение 1. Функции и графики в школьных учебниках Учебник Н.Я. Виленкин, 5 класс «Круговые диаграммы» 6 класс «Прямоугольная система В.И. Жохов, дают достаточное координатная плоскости, А.С. Чесноков, представление учащимся о абсцисса и ордината точки». С. И. Шварцбурд наглядном изображении Примеры графиков, диаграмм. «Математика» отдельных составных частей Учащиеся знакомятся с какой-нибудь величины. В прямоугольной системой упражнениях можно широко координат, учатся читать использовать статистический графики движений, материал, публикуемый в измерения температур и др. прессе. Г.В. Дорофеев, «Линии». При ее «Координаты». И.Ф. Шарыгин изучении у учащихся Прямоугольная система «Математика» формируются общие координат на плоскости, представления о линии и ее абсцисса и ордината точки. графическом представлении. Важно понимание сущности «Таблицы и диаграммы» координат, как способа формируется умение записи определения наглядно изобразить положения того или иного информацию в форме математического объекта. столбчатой диаграммы. И. И. Зубарева, «Координаты». А. Г. Мордкович, Прямоугольная система «Математика» координат на плоскости, абсцисса и ордината точки. Учащиеся учатся строить точки по указанным координатам. «Диаграммы». При изучении формируется умение наглядно изобразить информацию. Учебник 7 класс 8 класс 9 класс Ю. И. Функции: - функция у=k/x - квадратичная Макарычев -способы задания ее графики и функция; функции; свойства; - формирование -график функции; - функция у = x , умения находить -функция у=kх; ее свойства и по графику -функция у=kх+b; график; связь с промежутков - функции у=х2 , функцией у=х2 возрастания и и др. «Алгебра» у=х3; убывания, - их графики; промежутков - графический знакопостоянства; способ решения - решение систем уравнений. неравенств с одной переменной графическим способом; - степенная функция. Ш.А. Алимов Линейная функция и - построение - изучение «Алгебра» ее график. графика степенных При изучении этой квадратичной функций; темы учащиеся функции, изучение - функции у = х2; приобретают важные свойств у = х3; у= x ; умения читать квадратичной у=1/x; у=k/x; график. функции, - кроме - решение традиционных неравенств с примеров помощью графика. рассматривается моделирование реальных процессов, протекающих по законам линейной функции, - решение систем у = ах2 + bх + с; - формируется умение строить графики этих функций, вырабатывать умение устанавливать свойства (читать график) по уравнений заданному графическим графику. способом. Г.В. Дорофеев и - множества точек на - графики реальных - квадратичная др. «Математика» координатной зависимостей; функция; плоскости; - функции - свойства - графики у=kх+b; у = k/x их квадратичной зависимостей свойства и графики; функции. - у = х; - функциональная В системе у=\х\; терминология. упражнений - у = х 2 ; у =х 3 . Изложение строится значительное на основе работы с место занимают Акцент ставится на графиками реальных задачи умение считывать с зависимостей. прикладного графика нужную Представление в характера, информацию. общих свойствах которые решаются формируется при с опорой на рассмотрении графические графиков. представления. у = -х; - графический способ решения квадратичных неравенств; графический способ решения систем уравнений. К.С. Муравин, - функциональная - функция у = ах2, ее - графический Г. К. Муравин, символика; свойства и график; метод решения Г. В. Дорофеев - линейное уравнение « Алгебра» и его график; - функция у = k x систем рациональных - прямая ее свойства и выражений; пропорциональность график; - числовые и ее график; - построение функции. - взаимное графиков функций у Изучаются расположение = f(x+t), свойства функций, графиков линейных -график даются наглядно- функций; - функция у квадратичной геометрические = х2 и ее свойства и функции; представления о график; - построение и непрерывности, - функции, заданные чтение графиков выпуклости различными кусочных функций, функций. формулами на составленных из - обзор свойств и различных линейной и графиков всех промежутках квадратичной известных (кусочные функции); функций; функций; - графическое - графическое - функции y=xn, решение уравнений. решение y=x-n, их - понятие о уравнений; свойства и непрерывных и понятие графики; разрывных функциях квадратного корня рассматривается на вводиться примере кусочных используя график функций. функции. Ученик 10 класс 11 класс А.Н. Колмогоров и - тригонометрические - применение производной к др. «Алгебра и функции, их свойства и исследованию и построению начала анализа» графики; графика; - понятие асимптоты - показательная функция, ее графика. свойства и график; Особое внимание уделяется - площадь криволинейной графической интерпретации трапеции. свойств. - преобразование графиков; - графическая иллюстрация вывода формулы корней простейших тригонометрических уравнений. - графическая интерпретация понятия приращение аргумента, приращение функции; - геометрический смысл производной; - применение производной к исследованию функции. Ш.А. Алимов, - степенная функция, ее - тригонометрические Ю.М. Колягин, свойства и график; функции, их свойства и Ю.В. Сидоров и др. - показательная функция, ее графики; «Алгебра и начала свойства и график; - геометрический смысл анализа» - логарифмическая функция, производной; ее свойства и график. - применение производной к построению графиков функций; - нахождение площади криволинейной трапеции. А.Г. Мордкович - тригонометрические - вычисление площади «Алгебра и начала функции их свойства и криволинейной трапеции; анализа» графики; - функция у = n x , ее свойства - тригонометрические и график; уравнения. - степенные функции, их Формулы корней учащиеся свойства и график; выводят при работе с моделью «числовой окружности». - производная. Геометрическая модель предела функции на бесконечности. - Исследование и построение - показательная функция, ее свойства и график; функция у =logax, ее свойства и график. графика функции с помощью производной; -составление уравнения касательной к графику функции в точке.