Динамика вращательного движения

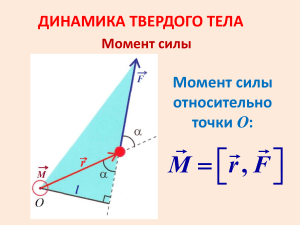
Динамика вращательного движения.
Основные понятия и формулы.
Момент силы относительно неподвижной точки
M   r , F  ,
где r – радиус-вектор, проведенный из этой точки в точку приложения
силы F .
Момент силы относительно неподвижной оси Z
M z   r , F  .
Модуль момента силы
M  Fl ,
где l – плечо силы (кратчайшее расстояние между линией
действия силы и осью вращения).
Момент инерции материальной точки
J  mr 2 ,
где m – масса точки; r – расстояние до оси вращения.
Момент инерции системы (тела)
n
J   mi ri2 ,
i 1
где ri – расстояние материальной точки массой mi до оси
вращения.
Ниже приведены моменты инерции некоторых однородных тел
массой m правильной геометрической формы.
Тело
Полый
тонкостенный
цилиндр
радиусом R
Сплошной
цилиндр
или диск
радиусом R
Прямой
тонкостенный
стержень длиной l
Положение оси
вращения
Ось симметрии
То же
Ось перпендикулярна
к стержню
и проходит через его
середину
Момент
инерции
mR 2
1
mR 2
2
1
ml 2
12
Ось перпендикулярна
к стержню
и проходит через его
конец
Ось проходит через
центр шара
То же
Шар радиусом R
1 2
ml
3
2
mR 2
5
В случае непрерывного распределения масс (сплошного
однородного твердого тела)
J   r 2 dm    r 2 dV ,
m
V
где  – плотность тела; V – его объем.
Теорема Штейнера
J  J c  ma 2 ,
где J c – момент инерции тела относительно оси, проходящей через
центр масс; J – момент инерции относительно параллельной оси,
отстоящей от первой на расстоянии a ; m – масса вращающегося тела.
Момент импульса материальной точки относительно неподвижной
точки
L   r , p   r , m .
Момент импульса (момент количества движения) твердого тела
относительно неподвижной оси вращения
n
Lz   mi i ri  J z z ,
i 1
где ri – расстояние от оси z до отдельной частицы тела; mi i –
импульс этой частицы; J z – момент инерции тела относительно оси Z ;
 z – угловая скорость вращения.
Закон сохранения момента импульса (момента количества
движения) для замкнутой системы
n
 Li  const .
i 1
Для двух взаимодействующих тел закон сохранения момента
импульса
J11  J 22  J11  J 2 2 ,
где J1 , J 2 , 1 , 2 – моменты инерции и угловые скорости тел до
взаимодействия; J1 , J 2 , 2 , 2 – те же величины после взаимодействия.
Основное уравнение (закон) динамики вращательного движения
твердого тела относительно неподвижной оси
d
dL
M z  Jz
 J z ,
;
dt
dt
где  – угловое ускорение; J z – момент инерции тела
M
относительно оси Z .
Элементарная работа при вращении тела
dA  M z d  ,
где d – угол поворота тела; M z – момент силы относительно оси
z.
Работа внешних сил при повороте твердого тела на конечный угол
φ

A   M zd .
0
Если M z = const, то работа
A  M z .
Кинетическая энергия тела, вращающегося вокруг неподвижной оси
Z,
J z 2
WКар 
,
2
где J z – момент инерции тела относительно оси Z ;  – его
угловая скорость.
Кинетическая энергия тела, катящегося по плоскости без
скольжения,
1
1
WK  mc2  J c2 ,
2
2
где m – масса тела; c – скорость центра масс тела; J c – момент
инерции тела относительно оси, проходящей через его центр масс;  –
угловая скорость тела.
Напряжение при упругой деформации тела

F
,
S
Где F – растягивающая (сжимающая) сила; S – площадь поперечного
сечения тела.
Относительное продольное растяжение (сжатие)

l
,
l
Где l – изменение длины тела при растяжении (сжатии); l – длина
тела до деформации.
Относительное поперечное растяжение (сжатие)
d
,
d
где d – изменение диаметра стержня при растяжении (сжатии);
 
d – диаметр стержня.
Связь между относительным поперечным сжатием (растяжением)
 и относительным продольным растяжением (сжатием)  :
   ,
где  – коэффициент Пуассона.
Закон Гука для продольного растяжения (сжатия)
  E ,
где E – модуль Юнга.
Потенциальная энергия упругорастянутого (сжатого) тела
W 
l

0
1 ES
E 2
2
Fdx 
(l ) 
V,
2 l
2
где V – объем тела.