Момент импульса, момент силы. Момент инерции. Теорема

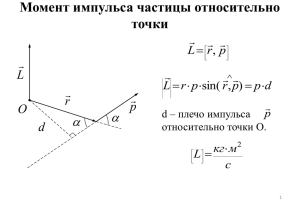
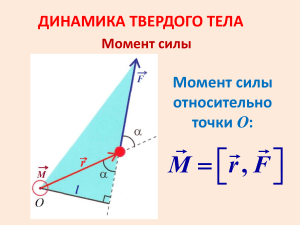
Момент импульса, момент силы. Момент инерции. Теорема Штейнера
Момент силы.
5.3.
К материальной точке, радиус – вектор которой относительно начала координат O раr
r
r
r
r
r
r
r
вен r = 3i + 4 j , приложена сила F = −2i + 1,5 j . Вычислите момент M и плечо l силы F относительно точки O.
Решение.
r
rr
По определению M = [r F ] . Вычисляем:
r
i
r
rr
M = [r F ] = x
Fx
r
j
y
Fy
r
r
r r
i
j k
k
r
4 0 = 12,5 ⋅ k .
z = 3
Fz − 2 1,5 0
r
r
Плечо силы определяется формулой M = lF , где M = M = 12,5 , F = F = 2 2 + 1,5 2 = 2,5 . Следовательно, l = M / F = 5 м.
Момент импульса материальной точки.
r
r
r
Радиус – вектор материальной точки относительно начала координат O равен r = 3i + 4 j . Имr
r
r
пульс этой материальной точки равен p = 2i . Вычислите момент импульса L материальной точки
относительно точки O.
5.10.
Решение.
r rr
По определению L = [r p] . Вычисляем:
r
i
r rr
L = [r p] = x
px
r
j
y
py
r
r r r
i j k
k
r
z = 3 4 0 = −8 ⋅ k .
pz 2 0 0
Сохранение момента импульса.
5.19. Частица движется в центральном поле сил с центром в
точке О (см. рис.). На рисунке показан участок траектории.
Считая известными v1 , α, r1, β и r2 , найдите v 2 .
Решение.
В центральном поле сил момент импульса относительно центра поля
(точка O на рис.) сохраняется, поскольку момент центральных сил
относительно точки O равен нулю. Проекция момента мпульса на ось Z , проходящую через точку O
перпендикулярно плоскости чертежа «от нас», равна:
Lz = υ1r1 sin α = υ 2 r2 sin β .
Поэтому
υ 2 = υ1
r1 sin α
.
r2 sin β
Момент сил, действующих на твердое тело
6.14. На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержr
r
ню прикладывают горизонтальные силы F1 и F2 как показано на рис.
Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
Решение.
r
F1
r
r
rr
r r
Векторы M 1 = [r1 F1 ] и M 2 = [r2 F2 ] направлены «на
нас» перепендикулярно плоскости чертежа. Учитыая,
что r1 = l / 4 , r2 = l / 2 и F1 = 2F2 , получим
r
r1
C
r
r2
M=
r
F2
l
l
F1 + F2 = F2 l .
4
2
Момент инерции твердого тела.
Теорема Штейнера
6.36 Найдите момент инерции тонкой однородной прямоугольной пластинки относительно
оси, перпендикулярной ее плоскости и проходящей через одну из ее вершин, если известно, что
момент инерции пластинки относительно параллельной оси, проходящей через ее центр, нахоm ⋅ a2 + b2
дится по формуле
. Масса пластинки m, длины ее сторон a и b.
12
(
)
Решение.
Момент инерции относительно оси 1, проходящей через центр масс, равен
m( a 2 + b 2 )
IC =
.
12
По теореме Штейнера момент инерции относительно
оси 2, параллельной оси 1, равен I 2 = I C + ml 2 ,
ось 1
ось 2
C
где l = (a / 2) 2 + (b / 2) 2 - расстояние между осями. После преобразований получим
m
I 2 = ⋅ (a 2 + b 2 ) .
3