1.4.Динамика твердого тела Момент инерции Момент инерции
реклама

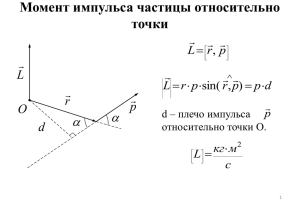
Момент инерции Момент инерции тела относительно неподвижной оси – физическая величина, равная сумме произведений элементарных масс на квадраты их расстояний до рассматриваемой оси и являющаяся мерой инертности тела во вращательном движении: n I mi ri 2 i 1 Суммирование производится по всем элементарным массам , на которые можно разбить тело. Момент инерции — величина аддитивная: момент инерции тела равен сумме моментов инерции его частей. Момент инерции тела в случае непрерывного распределения масс I r 2 dm r 2 dV где ρ - плотность тела в данной точке; dm=ρdV - масса малого элемента тела объемом dV, отстоящего относительно оси вращения на расстоянии r. Интегралы берутся по всему объему тела, причем величины ρ и r являются функциями точки (например, декартовых координат х, у и z). Момент инерции сплошного цилиндра Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr. Момент инерции каждого полого цилиндра dI r 2 dm , (dr r ). Объем элементарного цилиндра 2πrhdr, его масса dm = 2πrhρ dr и dI=2πhρr3 dr (ρ - плотность материала). Момент инерции сплошного цилиндра . R 1 I dI 2h r 3 dr hR 4 2 0 2 2 Поскольку R h - объем цилиндра, его масса m R h то момент инерции сплошного цилиндра: 1 I mR 2 2 http://www.youtube.com/watch?v=gO2CRb8FHLA&feature=related Теорема Штейнера Момент инерции тела I относительно любой оси вращения равен моменту его инерции Ic относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы m тела на квадрат расстояния а между осями. Моменты инерции однородных тел Тело Положение оси вращения Полый тонкостенный цилиндр радиуса R I mR2 Сплошной цилиндр или диск радиуса R 1 I mR2 2 Прямой тонкий стержень длиной l Шар радиуса R Прямоугольная тонкая пластинка со сторонами аиb Момент инерции I Ось проходит через центр шара 1 2 ml 12 2 I mR2 5 m( a 2 b 2 ) I 12 Кинетическая энергия вращающегося твердого тела Тело вращается вокруг неподвижной оси . Мысленно разбиваем это тело на элементарные массы m1 , m2 , ..., mi , ..., r1 , r2 , ..., ri , ... . При вращении находящиеся на расстоянии твердого тела элементарные объемы массами mi опишут окружности радиусов ri . Кинетическая энергия i-й элементарной массы mi i2 mi 2 ri 2 Eк i 2 2 Линейная скорость элементарной массы mi равна i ri (угловая скорость вращения всех элементарных объемов одинакова). Кинетическая энергия вращающегося твердого тела. n mi 2 2 2 n 2 Ек в р i 1 2 ri 2 m r i 1 i i I z 2 Eк вр 2 I z - момент инерции тела относительно оси z. Из сравнения формул следует, что момент инерции – мера инертности тела при вращательном движении. Плоское движение твердого тела Плоским называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Произвольное плоское движение можно представить как совокупность поступательного движения и вращения. Разбиение движения на поступательное и вращательное можно осуществить множеством способов, отличающихся значениями скорости поступательного движения, но соответствующих одной и той же угловой скорости . Поэтому можно говорить об угловой скорости вращения твердого тела, не указывая через какую точку проходит ось вращения. Тогда формула для скорости точек относительно неподвижной системы отчета будет иметь вид: V Vc r где Vc - скорость центра масс тела, ω - угловая скорость тела. Кинетическая энергия тела при плоском движении – складывается из энергии поступательного движения со скоростью, равной скорости центра масс, и энергии вращения вокруг оси, проходящей через центр масс тела. mVc2 I c 2 Eк 2 2 где m - масса тела; Ic - момент инерции тела относительно оси, проходящей через его центр масс. Момент силы Момент силы относительно неподвижной точки О физическая величина, определяемая векторным произведением радиуса-вектора r , проведенного из точки О в точку А приложения силы, на силу F M- М rF осевой вектор (псевдовектор), его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F . Модуль вектора момента силы M F r sin F l - угол между r и F , r sin l - кратчайшее расстояние между линией действия силы и точкой - плечо силы. Уравнение динамики вращательного движения Сила F приложена к точке В, находящейся от оси на расстоянии r , - угол между направлением силы и радиусом-вектором r . Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол d точка В приложения силы проходит путь r d и работа равна произведению проекции силы на направление смещения на величину смещения: d. A F sin r d Учитывая, что , M Z F r sin F l получаем d A M Z d . Работа вращения тела идет на увеличение его кинетической энергии: d A d Eк вр , d A M Z d , d Е d I I d . 2 Тогда d d IZ M Z d I Z d , или M Z . dt dt 2 Z к Z d Так как угловая скорость , то M Z I Z . dt Уравнение динамики твердого тела: M Z IZ вращательного движения . Момент сил твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловое ускорение. Аналогия в описании поступательного и вращательного движений Поступательное движение Масса m Вращательное движение Момент инерции I Скорость dr dt Угловая скорость d dt Ускорение d a dt Угловое ускорение d dt F Сила Основное уравнение F ma динамики Работа Кинетическая энергия M Момент силы dp F dt dA Fs ds m 2 2 Основное уравнение M I Z Z динамики Работа Кинетическая энергия dL M dt dA M Z d I Z 2 2 •Курс физики. Учебник для вузов/под. ред. проф. В.Н. Лозовского. СПб: Лань, 2009. Т.1 •Т.И. Трофимова. Краткий курс физики. Учебное пособие для вузов. М: КноРус, 2010. •Лозовский В.Н., Лозовский С.В. Концепции современного естествознания. Учебное пособие для вузов. - СПб: Лань, 2006. •Википедия http://ru.wikipedia.org/