φ α a x

y
φ
𝛚
⊙𝑧
α
a
𝑚𝑔
α
ℎ
𝛚
0
x
m
𝑉𝑟
β
𝑃
𝛷𝑐
𝛷𝑒
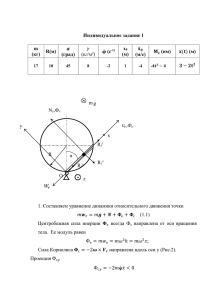
1) Составим уравнение динамики относительного движения точки
𝑚𝒘𝒓 = 𝑚𝒈 + 𝑵 + 𝚽е + 𝚽с (1.1)
Центробежная сила инерции 𝚽е всегда направлена от оси вращения тела. Ее
модуль равен
Фе = 𝑚𝑤𝑒 = 𝑚𝜔2 ℎ;
Сила Кориолиса 𝚽с = −2𝛚 × 𝑽𝒓 (направлена вдоль оси у)
Проекция Фс𝑦 = −2𝑚𝛗̇ 𝑥̇ < 0
Т.к 𝛗̇<0 и 𝑥̇ <0 , 𝛚 направлена от нас.(ось z на нас, т.к. φ против часовой)
Проектируем уравнение динамики на ось х, получаем
дифференциальное уравнение относительного движения точки.
𝑚𝑥̈ = Фе Cosβ = 𝑚𝜔2 ℎCosβ = 𝑚𝜔2 (𝑥 − 𝑎𝑆𝑖𝑛𝛼)
𝑥̈ − 𝜔2 x = −a𝑆𝑖𝑛𝛼
a𝑆𝑖𝑛𝛼 = 8 ∗ 𝑠𝑖𝑛45° = 5,66
𝑥̈ − 16x = −5,66
𝑥̈ − 16x = −5,66
2) Положение относительного равновесия находится в точке, где
ускорение равно нулю. Это точка Р с координатой:
ẍ = 0=> -16x=-5,66
x=0,35м
3) Найдем закон относительного движения и скорости точки. Это
обратная задача динамики. Решение неоднородного уравнения (1.1)
ищем в виде
𝑥 = 𝑥𝑜𝑜 + 𝑥ч
Решение однородного уравнения 𝑥𝑜𝑜 ищем в виде
𝑥𝑜𝑜 = 𝑒 𝜆𝑡 ;
Подставляя решение в однородное уравнение, приходим к
характеристическому уравнению с вещественными корнями
𝜆2 − 𝜔2 = 0;
𝜆1,2 = ±𝜔;
Решение принимает вид
𝑥𝑜𝑜 = 𝐶1 𝑒 𝜔𝑡 + 𝐶2 𝑒 −𝜔𝑡
Частное решение 𝑥ч ищем в виде правой части, т.е. постоянной
−𝜔2 𝑥ч = −𝑎𝜔2 𝑆𝑖𝑛𝛼;
𝑥ч = 𝑎𝑆𝑖𝑛𝛼
Полное решение уравнения динамики относительного движения точки
𝑥 = 𝐶1 𝑒 𝜔𝑡 + 𝐶2 𝑒 −𝜔𝑡 + 𝑎𝑆𝑖𝑛𝛼;
𝑥̇ = 𝜔𝐶1 𝑒 𝜔𝑡 − 𝜔𝐶2 𝑒 −𝜔𝑡
Постоянные 𝐶1 и 𝐶2 находим из начальных условий
t=0 ; x0 = 5 м; 𝑥̇ 0 = - 3 м/с
𝑎𝑆𝑖𝑛𝛼 = 5,66 = 𝑥ч
𝑥 = 𝐶1 + 𝐶2 + 5,66
{ 0
𝑥0̇ = 𝜔𝐶1 − 𝜔𝐶2
𝑥̇ 0
+ 𝐶2 = 𝐶1
𝜔
𝑥̇ 0
+ 2𝐶2 + 5,66;
𝜔
𝑥̇ 0
𝑥̇ 0
+ 𝐶2 = 𝐶1 𝑥0 = + 2𝐶2 + 5,66;
𝜔
𝜔
𝑥̇ 0
𝑥̇ 0
𝑥0 + − 5,66 = 2𝐶1 𝑥0 − − 5,66 = 2𝐶2 ;
𝜔
𝜔
1
𝑥̇ 0
1
𝑥̇ 0
𝑥 = (𝑥0 + − 5,66)𝑒 𝜔𝑡 + (𝑥0 − − 5,66)𝑒 −𝜔𝑡 + 5,66
2
𝜔
2
𝜔
𝑥0 =
1
𝑥̇ 0 1 𝜔𝑡
𝑥̇ 0
(𝑒 − 𝑒 −𝜔𝑡 ) = (𝑥0 − 5,66)𝑐ℎ𝑡 + 𝑠ℎ𝑡
𝑥 = (𝑥0 − 5,66) (𝑒 𝜔𝑡 + 𝑒 −𝜔𝑡 ) +
2
𝜔2
𝜔
С учетом начальных условий 𝛚 = 𝛗̇ = −𝟒 (1/с); 𝐱 𝟎 = 𝟓 м; 𝒙̇ 𝟎 = - 3 м/с
𝑥 = −0,66𝑐ℎ𝜔𝑡 + 0,75𝑠ℎ𝜔𝑡;
𝟏
𝟏
𝟐
𝟐
𝒔𝒉𝒕 = (𝒆𝝎𝒕 − 𝒆−𝝎𝒕 ); 𝒄𝒉𝒕 = (𝒆𝝎𝒕 + 𝒆−𝝎𝒕 )
𝑥̇ = 𝜔𝐶1 𝑒 𝜔𝑡 − 𝜔𝐶2 𝑒 −𝜔𝑡 = 𝜔(𝐶1 𝑒 𝜔𝑡 − 𝐶2 𝑒 −𝜔𝑡 ) =
5,66) 𝑒 𝜔𝑡 − (𝑥0 −
𝑥̇ 0
𝜔
1
2
𝜔 ((𝑥0 +
1
1
2
2
− 5,66) 𝑒−𝜔𝑡 ) = ω𝑥0 (𝑒 𝜔𝑡 − 𝑒 −𝜔𝑡 ) +
1
1
2
2
𝑒 −𝜔𝑡 ) + 2,83𝜔(𝑒 𝜔𝑡 − 𝑒 −𝜔𝑡 ) = 2,83𝜔2 (𝑒 𝜔𝑡 − 𝑒 −𝜔𝑡 ) +
𝑥̇ 0
𝜔
−
𝑥̇ 0 (𝑒 𝜔𝑡 +
𝑥̇ 0 (𝑒 𝜔𝑡 + 𝑒 −𝜔𝑡 ) =
45,3𝑠ℎ𝑡 − 3𝑐ℎ𝑡
𝑥̇ = 45,3𝑠ℎ𝑡 − 3𝑐ℎ𝑡
4. Найдем скорость точки в момент, когда она покидает тело. Можно
было бы и закона движения определить соответствующий момент
времени и подставить его в закон изменения скорости. Но проще найти
зависимость скорости точки от ее перемещения известной заменой
𝑑𝑥̇
𝑥̈ = 𝑥̇
𝑑𝑥
Которая фактически приводит к теореме об изменении кинетической
энергии точки.
Получаем
𝑥̈ − 𝜔2 x = −a𝑆𝑖𝑛𝛼
𝑥̈ = −a𝑆𝑖𝑛𝛼 + 𝜔2 x
𝑥̇
𝑑𝑥̇
= 𝜔2 x − a𝑆𝑖𝑛𝛼
𝑑𝑥
𝑥̇ 𝑑𝑥̇ = (𝜔2 x − a𝑆𝑖𝑛𝛼)𝑑𝑥
Интегрируя, находим зависимость относительной скорости точки от ее перемещения
𝑥̇ 2
2
=
𝜔2 𝑥 2
2
− ax𝑆𝑖𝑛𝛼+𝐶3
Находим 𝐶3 из начальных условий. 𝐶3 =
𝑥0̇ 2
2
−
𝜔2 𝑥0 2
2
𝐶3 =4,5-72+28=-39,5
𝑥̇ = √𝜔 2 𝑥 2 − 2ax𝑆𝑖𝑛𝛼 + 2𝐶3
Найдём 𝑥̇ при 𝑥 = 11,3(момент вылета, конец трубки)
+ ax0 𝑆𝑖𝑛𝛼
𝑥̇ = √16 ∗ 127.7 − 16 ∗ 11.3 ∗ 0.7 − 2 ∗ 39,5 = 42,9 м/с
5. Найдем закон изменения реакции тела на точку. Это прямая задача
динамики. Проекция уравнения (1.1) на ось z:
0 = 𝑁𝑧 − 𝑚𝑔;
дает проекцию реакции стержня на ось z
𝑁𝑧 = 𝑚𝑔
Проектируя уравнение (1.1) на ось у, находим:
0 = 𝑁𝑦 − Фе 𝑆𝑖𝑛β − Фсy ;
Теперь проекция нормальной реакции стержня на ось у равна
𝑁𝑦 =2𝑚𝛗̇𝑥̇ + 𝑚𝜔2 ℎ 𝑆𝑖𝑛β = 2𝑚𝛗̇𝑥̇ + 𝑚𝛗̇2 𝑎𝐶𝑜𝑠𝛼
Рассчитаем какой будет реакция трубки на тело в момент вылета
𝑁𝑧 = 𝑚𝑔 = 117,6 Н;
𝑁𝑦 = 2 ∗ 12 ∗ 4 ∗ 42.9 + 12 ∗ 16 ∗ 5,66 = 5205,1 Н
6. Составляющие реакции шарнира R найдем по известным ускорениям
тела и точки из теоремы о движении центра масс.
Представленная пластина – равносторонний прямоугольный треугольник,
от сюда следует, что его центр масс находиться в пересечении биссектрис.
Точка 0 (центр тяжести пластины) 2/3h, где h – перпендикуляр
опущенный от оси на край пластины
𝑹 = 𝑀𝒘𝒄
𝑀𝒘𝒄 = 𝑀1 𝒘𝒆1 + 𝑚𝒘 = 𝑹𝟏 + 𝑹𝟐
𝑚𝑔
где 𝑹𝟏 составляющая от ускорения
φ
𝛚
центра тяжести пластины, а 𝑹𝟑 от
𝑅1
a
α
ускорения точки. Последнее состоит
α
𝑅𝑒
0
из относительного, переносного и
𝑅𝑐
Кориолисова ускорений:
𝒉
𝑅𝑟
𝑹𝟒 = 𝑹𝑟4 + 𝑹𝑒4 + 𝑹𝑐4
0
m
2
1
2
3
2
3
𝑅1 = 𝑀1 𝜔2 ℎ=𝑐 ∗ 𝑎2 𝜔2 ∗ aCos45°=1,88 γ𝑎2 𝜔2
= 𝑚𝒘𝑟 + 𝑚𝒘𝑒 + 𝑚𝒘𝑐
𝑹𝑟2 = 𝑚𝑥̈ = 𝜔2 x − a𝐶𝑜𝑠𝛼 ; 𝑹𝑒2 = 𝜔2 h(ℎ − расстояние от оси до тела)
𝑹𝑐2 = 𝑚𝒘𝑐 = 2m 𝜔𝑉𝑟
Задание И2. Теорема об изменении кинетического момента.
Дифференциальное уравнение вращения тела. Условие равномерного
вращения.
1) Найдем закон изменения угловой скорости тела из теоремы об
изменении кинетического момента относительно оси вращения тела.
Кинетический момент системы складывается из кинетического момента
пластины с зафиксированной на ней в текущий момент точкой М и
кинетического момента точки М в относительном движении (плечо
aCosα=aSinα, (α=45º) aSinα=8 ∗
√2
=5,66
2
𝐾𝑧 = (𝐽пластины + 𝐽𝑚 )𝜑̇ − 𝑚𝑥̇ 𝑎𝑆𝑖𝑛𝛼
(2.1)
Последнее слагаемое положительно, поскольку при 𝑥̇ > 0 момент
относительной скорости сонаправлен со
y
стрелкой 𝜑.
φ
⊙𝑧
α
a
c
α
Пластина- четверть квадрата. Отсюда ¼
h
момента инерции и ¼ площади.
α
x
m
0
1
Jпластины = Jквадрата
4
β
с
Sпластины =
𝐽пластины =
Jпластины =
𝛷𝑒
a2
2
64
2
1
γa2
4
2
(32+32)
12
3
1
∗ ;(из таблицы
4
осевых моментов однородных пластин)
= Sквадрата ; mпластины=
∗
mпластины (c2 +b2 )
=170,6 кгм2
; b=aCosα=5,66 ; c=aSinα=5,66
𝐽𝑚 = 𝑚ℎ2 =12* (𝑎2 + 𝑥 2 − 2𝑎𝑥𝐶𝑜𝑠𝛼)=768+12(2 − 3𝑡 2 )2 −135,84(2-3𝑡 2 ) =
768 + 48 − 144𝑡 2 + 108𝑡 4 − 271,68 + 407,52𝑡 2 =544,32+263,52𝑡 2 + 108𝑡 4
; 𝑚𝑥̇ 𝑎𝑆𝑖𝑛𝛼 = 12 ∗ (−6𝑡) ∗ 5,66 = −407,5𝑡
Кинетический момент системы равен
𝐾𝑧 =(714,92+263,52𝑡 2 + 108𝑡 4 )𝜑̇ -407,5t
Интегрируем теорему об изменении кинетического момента
𝐾𝑧̇ = 𝑀𝑧 = −2𝑡 2 + 3;
Получаем
2𝑡 3
𝐾𝑧 = −
+ 3𝑡
3
От сюда (714,92+263,52𝑡 2 + 108𝑡 4 )𝜑̇ -407,5t = −
2𝑡 3
3
+ 3𝑡
2𝑡 3
+ 410,5𝑡
3
𝜑̇ =
(714,92 + 263,52𝑡 2 + 108𝑡 4 )
−
В момент, когда точка покидает тело.
x=2-3𝑡 2 =0 ; t 2 =
2
3
2
; 𝑡 = √ = 0,82 ; 𝜑̇ = 0,357 𝑐 −1 (посчитано в
3
маткаде, файл приложен к работе)
2. Найдем закон изменения движущей силы сцепления 𝑭сц , которая создается
мотором экипажа и обеспечивает заданное движение точки по телу. С
учетом силы 𝑭сц дифференциальное уравнение относительного движения
точки приобретает вид
𝑚𝑥̈ = 𝑚𝜔2 (𝑥 − 𝑎𝐶𝑜𝑠𝛼) + 𝐹𝑐ц
Отсюда находим закон изменения силы (𝑥̈ = −6) ; (𝑥 = 2 − 3𝑡 2 )
𝐹𝑐ц (𝑡) = 𝑚𝑥̈ + 𝑚𝜔2 (𝑎𝐶𝑜𝑠𝛼 − 𝑥) = −72 + [
2𝑡3
+410,5𝑡
3
(714,92+263,52𝑡 2 +108𝑡 4 )
−
2
] (3,66+3𝑡 2 )
3. Силу реакции 𝑵𝒚 точки на тело найдем из дифференциального уравнения
вращения тела.
𝐽пластины 𝜑̈ = 𝑀𝑧 + 𝑁𝑦 (𝑥 − 𝑎𝐶𝑜𝑠𝛼)
𝑁𝑦 =
𝐽пластины 𝜑̈ − 𝑀𝑧
𝑥 − 𝑎𝐶𝑜𝑠𝛼
Дифференцируя закон угловой скорости 𝜑̇ , получаем:
2𝑡 3
− 410,5𝑡) (527𝑡 + 432𝑡 3 )
3
[714,92 + 263,52𝑡 2 + 108𝑡 4 ]2
(−2𝑡 2 + 410,5)(714,92 + 263,52𝑡 2 + 108𝑡 4 ) + (
𝜑̈ =
Таким образом
2𝑡 3
3
(−2𝑡 2 + 410,5)(714,92 + 263,52𝑡 2 + 108𝑡 4 ) + (
3 − 410,5𝑡) (527𝑡 + 432𝑡 )
256 ∗ [
] + 2𝑡 2
[714,92 + 263,52𝑡 2 + 108𝑡 4 ]2
𝑁𝑦 =
2 − 3𝑡 2 − 𝑎𝐶𝑜𝑠𝛼
В момент вылета t=0,82
(Функция посчитана в маткаде, файл приложен к работе)
𝑁𝑦 = −7.823
4. Если тело вращается равномерно, значит сумма моментов всех сил,
действующих на тело, равна нулю. На тело, кроме момента 𝑀𝑧 , действует
сила давления, обратная по направлению силе 𝑁𝑦 , найденной в И1
(𝑁𝑦 =2𝑚𝛗̇𝑥̇ + 𝑚𝜔2 ℎ 𝑆𝑖𝑛β = 2𝑚𝛗̇𝑥̇ + 𝑚𝛗̇2 𝑎𝐶𝑜𝑠𝛼)
Следовательно
𝑁𝑦 = −𝑚𝛗̇ (2𝑥̇ + 𝛗̇ 𝑎𝐶𝑜𝑠𝛼)
Ее момент относительно оси z равен
𝑁𝑦 (𝑥 − 𝑎𝐶𝑜𝑠𝛼)
𝐱 𝐨̇
-3 м/с
α
45гр
𝝋̇
-4 1/с
−2𝑡 2 + 3
2 − 3𝑡 2
Приравнивая сумму моментов нулю
𝑀𝑧 + 𝑁𝑦 (𝑥 − 𝑎𝐶𝑜𝑠𝛼) = 0
находим закон изменения вращательного момента, поддерживающий
постоянную угловую скорость тела 𝛗̇ = −𝟒 𝒄−𝟏
𝑀𝑧 = −𝑁𝑦 (𝑥 − 𝑎𝐶𝑜𝑠𝛼) = 𝑚𝛗̇ (2𝑥̇ + 𝛗̇ 𝑎𝐶𝑜𝑠𝛼)(𝑥 − 𝑎𝐶𝑜𝑠𝛼) = 48(2𝑥̇ −
22,64)(𝑥 − 5,66) нм
y
φ
⊙𝑧
α
a
α
a
ℎ
𝑣𝑒 = ℎ𝜑̇
β
x
m
0
1. Найдем закон изменения
угловой скорости из уравнения
𝑣𝑟 = 𝑥̇
Лагранжа
𝑑 𝜕𝑇 𝜕𝑇
−
= 𝑄𝜑
𝑑𝑡 𝜕𝜑̇ 𝜕𝜑
Кинетическая энергия системы складывается из энергии тела и точки
𝑇 = 𝑇𝐴𝑂𝐵 + 𝑇𝑀 =
𝐽пластины 2 𝑚 2
𝜑̇ + 𝑣
2
2
𝒉𝟐 = (𝑎2 + 𝑥 2 − 2𝑎𝑥𝐶𝑜𝑠𝛼); 𝑱пластины = 256 кгм2
𝒙 = 2 − 3𝑡 2 ;
𝒙𝟐 = 4 − 12𝑡 2 + 9𝑡 4 ; 𝒙̇ = −6𝑡
𝑇 = 128𝝋̇𝟐 +
𝒎 𝟐
(𝒙̇ + 𝝋̇𝟐 (𝑎2 + 𝑥 2 − 2𝑎𝑥𝐶𝑜𝑠𝛼) − 2𝑥̇ 𝜑̇ 𝑎𝑆𝑖𝑛𝛼)
𝟐
T = 128φ̇2 + 216t 2 + 384φ̇2 + 24φ̇2 − 72t 2 φ̇2 + 54t 4 φ̇2 − 135,84φ̇2
+ 203,76t 2 φ̇2 − 407,52tφ̇
𝜕𝑇
= 0,
𝜕𝜑
𝜕𝑇
= 256φ̇ + 768φ̇ + 48φ̇ − 144t 2 φ̇ + 108t 4 φ̇ − 271,68φ̇ + 407,52t 2 φ̇ − 407,52t
𝜕𝜑̇
𝜕𝑇
𝜕𝜑̇
= 𝐾𝑧 = −
2𝑡 3
3
+ 3𝑡
256φ̇ + 768φ̇ + 48φ̇ − 144t 2 φ̇ + 108t 4 φ̇ − 271,68φ̇ + 407,52t 2 φ̇ − 407,52t = −
2𝑡 3
+ 3𝑡
3
2𝑡 3
−
+ 410,52𝑡
3
𝜑̇ =
800,32 + 263,52𝑡 2 + 108𝑡 4
Приходим к тому-же результату, что и в И2
При t=0.82 c
𝜑̇ = 0,328 𝑐 −1
Задание И5. Уравнений Лагранжа. Теорема об изменении кинетической
энергии в переносном движении
Из условий задачи aSinα=aCosα=5,66. Угол альфа = 45°. Значит углы при основании пластины равны
Дифференциальные уравнения движения системы найдем из уравнений Лагранжа. За обобщенные
координаты выберем x и φ.
Запишем соответствующие уравнения Лагранжа:
𝑑 𝜕𝑇 𝜕𝑇
−
= 𝑄𝑥 ;
𝑑𝑡 𝜕𝑥̇ 𝜕𝑥
𝑑 𝜕𝑇 𝜕𝑇
−
= 𝑄𝜑
𝑑𝑡 𝜕𝜑̇ 𝜕𝜑
(5.1)
Выражение кинетической энергии системы (4.2) позаимствуем из задания И4
𝑇 = 𝑇пластины + 𝑇𝑀 =
𝐽пластины 2 𝑚 2
𝜑̇ + 𝑣
2
2
𝑇 = 85.3𝝋̇𝟐 +
`
𝒎
𝟐
(𝒙̇ 𝟐 + 𝝋̇𝟐 (𝑎2 + 𝑥 2 −
2𝑎𝑥𝐶𝑜𝑠𝛼) − 2𝑥̇ 𝜑̇ 𝑎𝐶𝑜𝑠𝛼)
Производные по 𝑥:
φ
d ∂T
⊙𝑧
dt ∂ẋ
𝜕𝑇
α
a
𝑁𝑦
𝑣𝑒 = ℎ𝜑̇
α
a
β
𝑣𝑟 = 𝑥̇
= 𝑚𝜑̇ 2 (𝑥 − 5,66) (2)
Обобщённая сила 𝑄𝑥 = 0,
равна нулю, поскольку нет сил,
имеющих составляющие вдоль 𝒙
ℎ
α
m
0
𝜕𝑥
= 𝑚(𝑥̈ + 5,66𝝋̈𝒙̈ ) (1)
x
подставим (1) и (2)в ур-е Лагранжа
𝑚(𝑥̈ + 5,66𝝋̈𝒙̈ ) = 𝑚𝜑̇ 2 (𝑥 − 5,66) (3)
Поскольку.
𝜕𝑇
= 0;
𝑄𝜑 = 0
𝜕𝜑
то 𝜑 является циклической координатой, и ей соответствует циклический
интеграл дифференциального уравнения по 𝜑:
𝜕𝑇
= 170.6𝜑̇ + 𝑚(64𝜑̇ + 𝑥 2 𝜑̇ − 11.32𝑥𝜑̇ ) − 𝑚5,66𝑥̇ = 𝑐𝑜𝑛𝑠𝑡 (4)
̇
𝜕𝜑
Покажем, что циклический интеграл (4) выражает факт сохранение
кинетического момента системы относительно оси z. Согласно формуле (𝐾𝑧 )
задания И2
𝐾𝑧 = (𝐽пластины + 𝐽𝑚 )𝜑̇ − 𝑚𝑥̇ 𝑎𝑆𝑖𝑛𝛼
Подстановка данных задачи дает
𝐾𝑧 = 𝜑̇ (170.6 + 𝑚 ∗ (𝑎2 + 𝑥 2 − 2𝑎𝑥𝐶𝑜𝑠𝛼)) − 𝑥̇ 𝑚5,66
= 170.6𝜑̇ + 𝑚𝜑̇ (64 + 𝑥 2 − 5,66𝑥) − 𝑚5,66𝑥̇
Что полностью совпадает с выражением (4)
Значит (3) действительно выражает факт сохранение кинетического момента
системы относительно оси z. Ввиду начального покоя системы
𝐾𝑧 = 𝐶𝑜𝑛𝑠𝑡 = 0 (5)
Производная от (4) приводит к дифференциальному уравнению по 𝜑
𝑑 𝜕𝑇
= 170.6𝜑̈ + 𝑚64𝜑̈ + 𝜑̈ 𝑚𝑥 2 − 5.66𝑚𝑥𝜑̈ + 2𝑚𝜑̇ 𝑥̇ 𝑥 − 𝑚5,66𝑥̇ 𝜑̇ + 𝑚5,66𝑥̈
𝑑𝑡 𝜕𝜑̇
=0
1) При подстановке условий задачи 𝜑̇ = −4=const в уравнение (3)
𝑚(𝑥̈ + 5,66𝝋̈𝒙̈ ) = 𝑚𝜑̇ 2 (𝑥 − 5,66)
(6)
𝑥̈ = 16𝑥 − 90,56, что полностью соответствует уравнению в И1
2) Проверим закон угловой скорости тела, найденный в условиях задачи Б
При подстановке условий задачи Б при отсутствии момента 𝑀𝑧 : 𝑥 =
2 − 3𝑡 2 Проверим закон угловой скорости тела, найденный в условиях
задачи Б
При подстановке условий задачи Б при отсутствии момента 𝑀𝑧 : 𝑥 = 2 − 3𝑡 в (4)
2
получаем тот же закон угловой скорости. (m=12)
170.6𝜑̇ + 𝑚𝜑̇ (64 + (4 − 12𝑡 2 + 9𝑡 4 ) − 11.32(2 − 3𝑡 2 )) − 𝑚5.66(−6𝑡) =0
𝐾𝑧 = 0 = 𝜑̇ (170.6 + 768 + 48 − 144𝑡 2 + 108𝑡 4 − 271.68 + 407.52𝑡 2 ) + 407.52
𝐾𝑧 = 𝜑̇ (714.92 + 263.52𝑡 2 + 108𝑡 2 ) + 407.52 (такое − же как и в И2)
𝜑̇ =
3)
−407.5
(714.92 + 263.52𝑡 2 + 108𝑡 2 )
Общее выражение зависимости реакции
𝑵𝒚 тела на точку найдем из теоремы об изменении
кинетической энергии точки в переносном движении
𝑇1̇ + 2𝑇̇0 −
𝜕𝑇
= 𝑵𝒚 ∙ 𝒗𝑒
𝜕𝑡
(7)
Здесь использовано разложение выражения кинетической энергии точки Т на слагаемые по степеням
относительной скорости. Справа стоит мощность внешних сил (они здесь состоят из одной реакции
на переносном движении точки.
(из уравнения Т)
𝑵𝒚 )
𝑚
2
(𝒙̇ 𝟐 + 𝝋̇𝟐 (𝑎2 + 𝑥 2 − 2𝑎𝑥𝐶𝑜𝑠𝛼) − 2𝑥̇ 𝜑̇ 𝑎𝐶𝑜𝑠𝛼) = 𝑇2 + 𝑇1 + 𝑇0
Cosa=Sina
𝑇=
𝒎
𝟐
(𝒙̇ 𝟐 + 𝝋̇𝟐 (𝑎2 + 𝑥 2 − 2𝑎𝑥𝐶𝑜𝑠𝛼) − 2𝑥̇ 𝜑̇ 𝑎𝐶𝑜𝑠𝛼)
`
Кинетическая энергия Т не содержит
времени t, поэтому
𝜕𝑇
=0
𝜕𝑡
φ
Энергия T1 , содержащая 𝑥̇ в первой
степени и ее производная
𝑻𝟏 = −𝒎𝒙̇ 𝝋̇𝒂𝑪𝒐𝒔𝜶
⊙𝑧
a
α
α
a
ℎ
𝑣𝑒 = ℎ𝜑̇
Энергия T0 , содержащая 𝑥̇ в нулевой
β
m
0
𝑻𝟏̇ = −𝒎𝒂(𝒙̈ 𝝋̇ + 𝒙̇ 𝝋̈)𝑪𝒐𝒔𝒂
x
степени и ее производная (Cosα=Sinα)
𝑣𝑟 = 𝑥̇
𝑇0 =
m 𝟐 2
𝝋̇ (𝑎 + 𝑥 2 − 2𝑎𝑥𝑆𝑖𝑛𝛼) ; 𝑇0̇
2
= m𝝋̈(𝑎2 + 𝑥 2 − 2𝑎𝑥𝑆𝑖𝑛𝛼) + m𝝋̇𝟐 (𝑥𝑥̇ − 𝑎𝑥̇ 𝑆𝑖𝑛𝛼)
2𝑇0̇ = 2m𝝋̈(𝑎2 + 𝑥 2 − 2𝑎𝑥𝑆𝑖𝑛𝛼) + 2m𝝋̇𝟐 (𝑥𝑥̇ − 𝑎𝑥̇ 𝑆𝑖𝑛𝛼)
𝑵𝒚 ∙ 𝒗𝑒 = −𝑵𝒚 𝝋̇𝒉𝑪𝒐𝒔𝜷 = −𝑵𝒚 𝝋̇(𝒂𝑺𝒊𝒏𝒂 − 𝒙) (8)
𝑵𝒚 ∙ 𝒗𝑒 = 𝑇1̇ + 2𝑇̇0 −
𝜕𝑇
𝜕𝑇
, где
= 0, от сюда
𝜕𝑡
𝜕𝑡
𝑵𝒚 ∙ 𝒗𝑒 = 2m𝝋̈(𝑎2 + 𝑥 2 − 2𝑎𝑥𝑆𝑖𝑛𝛼) + 2m𝝋̇𝟐 (𝑥𝑥̇ − 𝑎𝑥̇ 𝑆𝑖𝑛𝛼) − 𝒎𝒂(𝒙̈ 𝝋̇ + 𝒙̇ 𝝋̈)𝑪𝒐𝒔𝒂)
(9)
Сопоставим (8)и (9)
−𝑵𝒚 𝝋̇(𝒂𝑺𝒊𝒏𝒂 − 𝒙)
= 2m𝝋̇𝝋̈(𝑎2 + 𝑥 2 − 2𝑎𝑥𝑆𝑖𝑛𝛼) + m𝝋̇𝟐 (𝑥𝑥̇ − 𝑎𝑥̇ 𝑆𝑖𝑛𝛼) − 𝒎𝒂(𝒙̈ 𝝋̇ + 𝒙̇ 𝝋̈)𝑪𝒐𝒔
Проверим выражение (для реакции Ny в условиях задачи А, где: 𝜑̇ = −4 =
𝐶𝑜𝑛𝑠𝑡, 𝜑̈ = 0 )
2m𝝋̈(𝑎2 + 𝑥 2 − 2𝑎𝑥𝑆𝑖𝑛𝛼) + 2m𝝋̇𝟐 (𝑥̇ − 𝑎𝑥̇ 𝐶𝑜𝑠𝛼) − 𝒎𝒂(𝒙̈ 𝝋̇ + 𝒙̇ 𝝋̈)𝑪𝒐𝒔𝒂
𝑁𝒚 =
𝝋̇(𝒂𝑺𝒊𝒏𝒂 − 𝒙)
2m𝝋̇𝟐 (𝑥𝑥̇ − 𝑎𝑥̇ 𝑆𝑖𝑛𝛼) − 𝒎𝒂𝒙̈ 𝝋̇𝑪𝒐𝒔𝒂
𝑁𝒚 =
𝝋̇(𝒂𝑺𝒊𝒏𝒂 − 𝒙)
̇ − x)
Дифференциальное уравнение движения 𝑥̈ = φ̇2 (aSinα
(𝑚𝑥̈ = Фе Cosβ = 𝑚𝜔2 ℎCosβ = 𝑚𝜔2 (𝑥 − 𝑎𝑆𝑖𝑛𝛼) ; 𝑥̈ − 𝜑̇ 2 x = −φ̇2 a𝑆𝑖𝑛𝛼
) Из И1
𝟐𝒎𝝋̇𝟐 𝒙̇ (𝒙 − 𝒂𝑺𝒊𝒏𝒂) − 𝒎𝒂φ̇3 (aSinα − x)Cosa
𝑁𝒚 =
−𝝋̇(𝒂𝑺𝒊𝒏𝒂 − 𝒙)
𝑁𝒚 = 𝟐𝒎𝝋̇𝒙̇ + 𝒎𝝋̇𝟐 𝒂𝑪𝒐𝒔𝒂
что сходится с И1