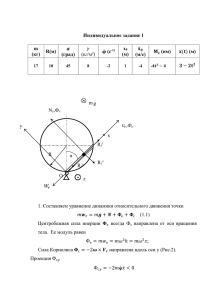
Задача А

1
m (кг)
R(м)
𝛼 (град)
18
6
-
Данные для задач А, Б и В
𝛾 (кг/м2) 𝛗̇ (c-1) x0 (м) 𝒙̇ 𝟎 (м/с)
8
-2
5
-3
𝑴𝒛 (нм)
𝒙(𝒕) (м/с)
-3t3+2
𝟒 − 𝟐𝒕𝟑
Задача А
Тело вращается с постоянной угловой скоростью
𝝋̇.
Найти
1. Дифференциальное уравнение
относительного движения точки.
2. Положение относительного равновесия,
если оно
существует.
3. Закон относительного движения и скорости
Рис.1
точки.
4. Скорость точки в момент, когда точка
покидает тело
5. Закон изменения реакции тела на точку и ее
значение в момент, когда точка покидает тело.
6. Выражения для составляющих главного вектора реакций шарниров тела.
Задание И1. Основное уравнения динамики относительного движения точки. Теорема о
движении центра масс системы.
1. Составляем уравнение динамики относительного движения точки
𝑚𝒘𝒓 = 𝑚𝒈 + 𝑵 + 𝚽е + 𝚽с (1.1)
Центробежная сила инерции 𝚽е всегда
направлена от оси вращения тела. Ее модуль
равен
Фе = 𝑚𝑤𝑒 = 𝑚𝜔2 𝑙;
Сила Кориолиса 𝚽с = −2𝑚𝛚 × 𝑽𝒓 направлена
вдоль оси у (Рис.2).
Проекция Фс𝑦
Рис.2
Фс𝑦 = −2𝑚𝛗̇𝑥̇ > 0
поскольку 𝑥̇ > 0, а 𝛗̇ < 𝟎.
Точка движется от начала х
Проектируя уравнение (1.1) на ось х, получаем дифференциальное уравнение
относительного движения точки
𝑚𝑥̈ = Фе Cosβ = 𝑚𝜔2 (𝑥 − 𝑅)
𝑥̈ − 𝜔2 𝑥 = −𝜔2 𝑅
или
𝑥̈ − 4𝑥 = −24
(1.2)
2. Положение относительного равновесия находится в точке, где ускорение равно нулю. Это
точка Р с координатой
𝑥 = 𝑥 0 = 𝑅 = 6м
При 𝑥0 > 𝑥 0 и 𝑥̇ 0 > 0 точка будет удаляться от начала О координаты 𝑥. При 𝑥0 < 𝑥 0 и
𝑥̇ 0 < 0 точка будет приближаться к началу О координаты х. При заданных начальных
условиях точка движется к началу координатной оси х.
2
3. Найдем закон относительного движения и скорости точки. Это обратная задача
динамики. Решение неоднородного уравнения (1.2) ищем в виде суммы общего решения
однородного уравнения 𝑥𝑜𝑜 и частного решения 𝑥ч уравнения (1.2)
𝑥 = 𝑥𝑜𝑜 + 𝑥ч
Общее решение однородного уравнения
𝑥̈ − 𝜔2 𝑥 = 0
ищем в виде
𝑥𝑜𝑜 = 𝑒 𝜆𝑡 ;
Подставляя это решение в однородное уравнение, приходим к характеристическому
уравнению с вещественными корнями
𝜆2 − 𝜔2 = 0; 𝜆1,2 = ±𝜔;
Решение 𝑥𝑜𝑜 принимает вид
𝑥𝑜𝑜 = 𝐶1 𝑒 𝜔𝑡 + 𝐶2 𝑒 −𝜔𝑡
Частное решение ищем в виде правой части, т.е. постоянной 𝑥ч = 𝐶𝑜𝑛𝑠𝑡. Подставив 𝑥ч в
уравнение (1.2), получим
−𝜔2 𝑥ч = −𝜔2 𝑅;
𝑥ч = 𝑅
Полное решение уравнения (1.2)
𝑥 = 𝐶1 𝑒 𝜔𝑡 + 𝐶2 𝑒 −𝜔𝑡 + 𝑅;
𝑥̇ = 𝜔𝐶1 𝑒 𝜔𝑡 − 𝜔𝐶2 𝑒 −𝜔𝑡 (1.3)
Постоянные 𝐶1 𝐶2 в (1.3) находим из начальных условий
𝑡 = 0: 𝑥0 = 5 м; 𝑥̇ 0 = −3 м/с (1.4)
Подставив (1.4) в (1.3), получим:
𝑥0 = 𝐶1 + 𝐶2 + 𝑅;
𝑥̇ 0 = 𝜔(𝐶1 − 𝐶2 )
Иначе
𝑥̇ 0
𝑥̇ 0
+ 𝐶2 = 𝐶1 𝑥0 = + 2𝐶2 + 𝑅;
𝜔
𝜔
𝑥̇ 0
𝑥̇ 0
𝑥0 + − 𝑅 = 2𝐶1 𝑥0 − − 𝑅 = 2𝐶2 ;
𝜔
𝜔
Решение приобретает вид
1
𝑥̇ 0 1 𝜔𝑡
𝑥̇ 0
(𝑒 − 𝑒 −𝜔𝑡 ) + 𝑅 = (𝑥0 − 𝑅)𝑐ℎ𝜔𝑡 + 𝑠ℎ𝜔𝑡 + 𝑅
𝑥 = (𝑥0 − 𝑅) (𝑒 𝜔𝑡 + 𝑒 −𝜔𝑡 ) +
2
𝜔2
𝜔
С учетом начальных условий (1.4)
𝑥 = −𝑐ℎ𝑡 − 1,5𝑠ℎ𝑡 + 𝑅;
𝑥̇ = −𝑠ℎ𝑡 − 1,5𝑐ℎ𝑡 (1.5)
4. Найдем скорость точки в момент, когда она покидает тело. Можно было бы из закона
движения определить соответствующий момент времени и подставить его в закон
изменения скорости. Но проще найти зависимость скорости точки от ее перемещения
известной заменой
𝑑𝑥̇
𝑥̈ = 𝑥̇
𝑑𝑥
Которая фактически приводит к теореме об изменении кинетической энергии точки.
Получаем
𝑑𝑥̇
𝑥̇
= 𝜔2 𝑥 − 𝜔2 𝑅; или 𝑥̇ 𝑑 𝑥̇ = (𝜔2 𝑥 − 𝜔2 𝑅)𝑑𝑥
𝑑𝑥
Интегрируя, находим зависимость относительной скорости точки от ее перемещения
𝑥̇ 2 = 𝜔2 𝑥(𝑥 − 2𝑅) + 𝐶3 (1.6)
Из начальных условий (1.4) находим
𝐶3 = 𝑥̇ 0 2 + 𝜔2 𝑥0 (2𝑅 − 𝑥0 ) = 9 + 20(12 − 5) = 149 м2 /с2
Находим скорость при 𝑥1 = 0 = 0м
3
𝑥̇ 1 = √0(0 − 12) + 149 = 12,2 м/с
Шарик вылетает справа, т.к. по формуле (1.5) 𝑥̇ <0
5. Найдем закон изменения реакции тела на точку. Это прямая задача динамики.
Проекция уравнения (1.1) на ось z:
0 = 𝑁𝑧 − 𝑚𝑔;
дает проекцию реакции стержня на ось z
𝑁𝑧 = 𝑚𝑔
(1.7)
Проектируя уравнение (1.1) на ось у, находим:
0 = 𝑁𝑦 − Фе 𝑆𝑖𝑛β + Фсy ;
Теперь проекция нормальной реакции стержня на ось у равна
𝑁𝑦 = 2𝑚𝛗̇𝑥̇ + 𝑚φ̇2 𝑙𝑆𝑖𝑛β = 𝑚𝛗̇(2𝑥̇ + 𝛗̇𝑅) = −72𝑥̇ + 432 н (1.8)
𝑁𝑦 зависит от найденной относительной скорости точки (1.5).
В момент, когда точка покидает тело
𝑁𝑧 = 𝑚𝑔 = 176,4 н;
𝑁𝑦 = 𝑚𝛗̇(2𝑥̇ 1 + 𝛗̇𝑅)|𝑥=𝑥1 = −36(24,4 − 12) = −446.4 н
(1.9)
6. Составляющие реакции шарнира R найдем по известным ускорениям тела и точки из
теоремы о движении центра масс
𝑹 = 𝑀𝒘𝒄
Это прямая задача динамики.
𝑀𝒘𝒄 = 𝑀1 𝒘𝒄1 + 𝑚𝒘 = 𝑹𝟏 + 𝑹𝟐
где 𝑹𝟏 составляющая от ускорения центра тяжести
пластины, а 𝑹𝟐 от ускорения точки. Последнее
состоит из относительного, переносного и
Кориолисова ускорений:
𝑹𝟐 = 𝑹𝑟2 + 𝑹𝑒2 + 𝑹𝑐2 = 𝑚𝒘𝑟 + 𝑚𝒘𝑒 + 𝑚𝒘𝑐
Направления составляющих изобразим на рисунке
и вычислим их величину
Рис.3
𝑅1 = γπR3 𝜔2 ;
𝑅2𝑒 = 𝑚𝜔2 √2𝑅
𝑅2𝑟 = 𝑚𝑥̈ = 𝑚𝜔2 𝑅
𝑅2𝑐 = 𝑚𝑤𝑐 = 2𝑚𝜔𝑥̇ 1
(1.10)
4
Задача Б
Тело вращается из состояния покоя под
действием момента 𝑴𝒛 . Самодвижущийся экипаж М,
принимаемый за точку массы m, движется без
сопротивления по закону 𝒙(𝒕) за счет силы
сцепления с телом.
Найти
1. Закон угловой скорости тела и ее значение в
момент, когда точка
покидает тело.
2. Закон силы сцепления 𝐅сц точки с телом,
обеспечивающей
заданное движение точки
3. Закон силы реакции тела на точку и ее
значение в момент вылета точки с тела.
4. В задаче А найти закон вращательного момента 𝐌𝐳 ,
обеспечивающий равномерное вращение тела
Задание И2. Теорема об изменении кинетического момента. Дифференциальное
уравнение вращения тела. Условие равномерного вращения.
1. Найдем закон изменения угловой скорости тела из теоремы об изменении кинетического
момента относительно оси вращения тела.
Кинетический момент системы складывается из кинетического момента диска с
зафиксированной на нем в текущий момент точкой m и кинетического момента точки m в
относительном движении (плечо 𝑅).
𝐾𝑧 = (𝐽диск + 𝐽𝑚 )𝜑̇ + 𝑚𝑥̇ 𝑅
(2.1)
𝐽диск вычисляется по формуле Штейнера
𝑚𝑅 2
𝐽диск =
+ 𝑚𝑅 2 = 𝐶𝑜𝑛𝑠𝑡
(2.2)
2
1
32555,52
𝐽диск = γπR4 + γπR4 =
+ 32555,52 = 48833.28 кгм2
2
2
(γ условились принимать как кг/м2 ) Момент инерции точки в текущем положении
𝐽𝑚 = 𝑚(𝑅 2 + (𝑥 − 𝑅)2 ) = 𝑚(2𝑅 2 + 𝑥 2 − 2𝑅𝑥) = 𝟏𝟖(𝟕𝟐 + 𝟏𝟔 − 𝟏𝟔𝐭 𝟑 + 4𝑡 6 − 48 + 24𝑡 3 )
= 18(40 + 8𝑡 3 + 4𝑡 6 ) = 720 + 144𝑡 3 + 72𝑡 6 кгм2 ;
Итак
𝐽 = 𝐽диск + 𝐽𝑚 = 49553.28 + 144𝑡 3 + 72𝑡 6 кгм2
(2.3)
Кинетический момент системы равен:
𝐾𝑧 = (49553.28 + 144𝑡 3 + 72𝑡 6 )𝜑̇ − 648𝑡 3
(2.4)
Интегрируем теорему об изменении кинетического момента
𝐾𝑧̇ = 𝑀𝑧 = −3𝑡 3 + 2;
Получаем
𝑡4
𝐾𝑧 = −3 + 2𝑡
(2.5)
4
Иначе
𝑡4
(49553.28 + 144𝑡 3 + 72𝑡 6 )𝜑̇ − 648𝑡 3 = −3 + 2𝑡
4
Отсюда находим закон угловой скорости тела
2𝑡 − 0,75𝑡 4 + 648𝑡 3
𝜑̇ =
(2.6)
49553.28 + 144𝑡 3 + 72𝑡 6
5
В момент, когда точка покидает тело.
𝑥1 = 4 − 2𝑡1 3 = 0;
3
𝑡1 = √2 𝑐,
𝜑̇ 1 =
1296,625
= 0,026 с−1
50129,28
(2.7)
2. Найдем закон изменения движущей силы сцепления 𝑭сц , которая создается мотором
экипажа и обеспечивает заданное движение точки по телу. С учетом силы 𝑭сц
дифференциальное уравнение относительного движения точки (1.2) приобретает вид
𝑚𝑥̈ = 𝑚𝜔2 (𝑥 − 𝑅) + 𝐹𝑐ц
(2.8)
Отсюда находим закон изменения силы
2
2𝑡 − 0,75𝑡 4 + 648𝑡 3
𝐹𝑐ц (𝑡) = 𝑚𝑥̈ + 𝑚𝜔
− 𝑥) = −216𝑡 + 36 [
] ∙ ( 1 + 𝑡 3 ) (2.9)
49553.28 + 144𝑡 3 + 72𝑡 6
3. Силу реакции 𝑁𝑦 точки на тело найдем из дифференциального уравнения вращения тела.
𝐽диск 𝜑̈ = 𝑀𝑧 + 𝑁𝑦 (𝑥 − 𝑅)
(2.10)
Или
𝐽диск 𝜑̈ = −3𝑡 3 + 2 + 𝑁𝑦 (𝑥 − 6)
(2.11)
Отсюда
𝐽диск 𝜑̈ + 3𝑡 3 − 2
𝑁𝑦 =
(2.12)
𝑥−6
Дифференцируя закон угловой скорости 𝜑̇ , получаем:
2 − 3𝑡 3 + 1944𝑡 2
432𝑡 2 (2𝑡 − 0,75𝑡 4 + 648𝑡 3 )(1 + 𝑡 3 )
𝜑̈ =
−
49553,28 + 144𝑡 3 + 72𝑡 6
(49553,28 + 144𝑡 3 + 72𝑡 6 )2
99106,56 + 96331576,32𝑡 2 − 149239,84𝑡 3 − 832𝑡 6 + 108𝑡 9 − 139968𝑡 8
=
(2.13)
(49553,28 + 144𝑡 3 + 72𝑡 6 )2
2 (𝑅
48833.28(
Таким образом 𝑁𝑦 =
99106,56+96331576,32𝑡2 −149239,84𝑡3 −832𝑡6 +108𝑡9 −139968𝑡8
)+3𝑡 3 −2
2
(49553,28+144𝑡3 +72𝑡6 )
−2−2𝑡 3
(2.14)
3
В момент вылета точки 𝑡1 = √2 𝑐 и
2950,76 + 4
𝑁𝑦1 =
= −492.46 н
−6
(2.15)
4. В задаче А тело вращается равномерно, значит сумма моментов всех сил, действующих на
тело, равна нулю. На тело, кроме момента 𝑀𝑧 , действует сила давления, обратная по
направлению силе 𝑁𝑦 , найденной в задаче А
𝑁𝑦 = −𝑚𝛗̇(2𝑥̇ − 𝛗̇𝑅)
Ее момент относительно оси z равен
𝑁𝑦 (𝑥 − 𝑅)
Приравнивая сумму моментов нулю
𝑀𝑧 + 𝑁𝑦 (𝑥 − 𝑅) = 0
(2.16)
находим закон изменения вращательного момента, поддерживающий постоянную угловую
скорость тела
𝑀𝑧 = −𝑁𝑦 (𝑥 − 𝑅) = 𝑚𝛗̇(2𝑥̇ − 𝛗̇𝑅)(𝑥 − 𝑅) = 18𝛗̇(2𝑥̇ − 𝛗̇6)(𝑥 − 6) нм (2.17)
где законы относительного движения 𝑥 и скорости точки 𝑥̇ являются известными функциями
времени, а функция 𝛗̇ была найдена ранее(1.5).
6
Задание И3. Уравнения Лагранжа. Теорема об изменении кинетической энергии.
1. Методом Лагранжа получить дифференциальное уравнение относительного
движения точки, найденное в И1.
2. С помощью теоремы об изменении кинетической энергии найти реакцию тела на
точку, и сравнить ее с результатом в И1.
Решение
1. Найдем дифференциальное уравнение относительного движения точки из уравнения
Лагранжа
𝑑 𝜕𝑇 𝜕𝑇
𝑚
−
= 𝑄𝑥 , (3.1)
𝑇 = 𝑉2
𝑑𝑡 𝜕𝑥̇ 𝜕𝑥
2
Абсолютная скорость V точки складывается из переносной и относительной скоростей
𝑉 2 = 𝑥̇ 2 + 𝑣𝑒 2 + 2𝑥̇ 𝑣𝑒 𝑆𝑖𝑛β,
𝑣𝑒 = 𝜔𝑙, 𝑙 = √𝑅 2 + (𝑥 − 𝑅)2 ; 𝑙𝑆𝑖𝑛β = 𝑅 (3.2)
Нет рисунка
Таким образом, кинетическая энергия приобретает выражение
𝑚
𝑇 = (𝑥̇ 2 + 𝜔2 (𝑅 2 + (𝑥 − 𝑅)2 ) + 2𝑥̇ 𝜔 𝑅)
(3.3)
2
Находим производные:
𝜕𝑇
𝑑 𝜕𝑇
𝜕𝑇
= 𝑚(𝑥̇ + 𝜔𝑅);
= 𝑚𝑥̈ ;
= 𝑚𝜔2 (𝑥 − 𝑅);
𝜕𝑥̇
𝑑𝑡 𝜕𝑥̇
𝜕𝑥
Обобщенная сила 𝑄𝑥 = 0 поскольку сила тяжести перпендикулярна скорости точки и не
имеет мощности.
Подставив производные в уравнение Лагранжа приходим к дифференциальному
уравнению (1.2), найденному в И1
𝑥̈ − 𝜔2 𝑥 = −𝜔2 𝑅
(3.4)
2. Реакцию 𝑁𝑦 тела на точку найдем из теоремы об изменении кинетической энергии
точки.
𝑇̇ = 𝑁
где N- мощность физических сил, приложенных к точке, в переносном и в относительном
движениях точки.
𝑁 = 𝑁𝜑 + 𝑁𝑥
Физических сил, имеющих проекцию на ось 𝑥 нет, поэтому
𝑁𝑥 = 𝑄𝑥 𝑥̇ = 0
Во вращательном переносном движении точки мощность реакции вычисляем через момент
𝑁𝜑 = 𝑚𝑧 (𝑵𝑦 )𝜑̇ ;
В соответствии с Рис.2
𝜕𝑇
𝜕𝑇
𝑇̇ =
𝑥̈ +
𝑥̇ = 𝑚(𝑥̇ + 𝜔𝑅)𝑥̈ + 𝑚𝜔2 (𝑥 − 𝑅)𝑥̇ = 𝑁𝒚 𝜔(𝑥 − 𝑅)
𝜕𝑥̇
𝜕𝑥
Из дифференциального уравнения (3.4)
𝑥̈ = 𝜔2 (𝑥 − 𝑅)
Таким образом, после сокращения на 𝜔(𝑥 − 𝑅) находим тот же результат, что и в И1
𝑁𝑦 = 𝑚𝜔(2𝑥̇ + 𝜔𝑅) = − 72𝑥̇ + 432 н
(3.5)
Ответ задачи А
1
2
3
4
5
0
𝑁𝑦
𝑥̈ − 4𝑥 = −24
𝑥 = 5м 𝑥 = −𝑐ℎ𝑡 − 1,5𝑠ℎ𝑡 + 𝑅 𝑣1
𝑥̇ = −𝑠ℎ𝑡 − 1,5𝑐ℎ𝑡
= 12,2 м/с = − 72𝑥̇ + 432 н
7
𝑁𝑦1 = 446,4 н
ve
Задание И4. Уравнения Лагранжа.
1. Найдем закон изменения угловой скорости из уравнения Лагранжа
𝑑 𝜕𝑇 𝜕𝑇
−
= 𝑄𝜑
(4.1)
𝑑𝑡 𝜕𝜑̇ 𝜕𝜑
Кинетическая энергия системы складывается из энергии диска и точки
𝐽диск 2 𝑚 2
𝑇 = 𝑇диск + 𝑇𝑀 =
𝜑̇ + 𝑣
2
2
𝑚
2
= 24416.64𝜑̇ + (𝑥̇ 2 + 𝜑̇ 2 (𝑅 2 + (𝑥 − 𝑅)2 ) + 2𝑥̇ 𝜑̇ 𝑅)
2
(4.2)
Подставив данные задачи, находим
𝑇 = 24416.64𝜑̇ 2 + 9{36𝑡 4 + 𝜑̇ 2 [36 + 16 − 16𝑡 3 + 4𝑡 6 − 12(4 − 2𝑡 3 ) + 36] + 𝟏𝟐𝜑̇ (−6𝑡 2 )}
= 24416.64𝜑̇ 2 + 9{36𝑡 4 + 𝜑̇ 2 [40 + 8𝑡 3 + 4𝑡 6 ] − 𝟕𝟐𝜑̇ 𝑡 2 }(4.3)
Обобщенная сила 𝑄𝜑 = 𝑀𝑧 = −3𝑡 3 + 2
(4.4)
𝜕𝑇
𝜕𝑇
3𝑡 4
= 0,
= 48833.28𝜑̇ + 18𝜑̇ [40 + 8𝑡 3 + 4𝑡 6 ] − 648𝑡 2 = −
+ 2𝑡
𝜕𝜑
𝜕𝜑̇
4
Приходим к тому же результату, что и в И2:
2𝑡 − 0,75𝑡 4 + 648𝑡 2
1296,625
𝜑̇ =
; 𝜑̇ 1 =
= 0,026 с−1
3
6
49553.28 + 144𝑡 + 72𝑡
50129,28
Ответ задачи Б
1
2
(4.5)
4
8
𝜑̇
2𝑡 − 0,75𝑡 4 + 648𝑡 2
=
49553.28 + 144𝑡 3 + 72𝑡 6
𝜑̇ 1 = 0,026 с−1
𝐹𝑐ц (𝑡) = 𝑚𝑥̈ + 𝑚𝜔2 (𝑅 − 𝑥)
= −216𝑡
2
2𝑡 − 0,75𝑡 4 + 648𝑡 2
+ 36 [
]
49553.28 + 144𝑡 3 + 72𝑡 6
∙ ( 1 + 𝑡3)
𝑀𝑧 = −𝑁𝑦 (𝑥 − 𝑅) = 𝑚𝛗̇(2𝑥̇ − 𝛗̇𝑅)(𝑥 − 𝑅)
= 18𝛗̇(2𝑥̇ − 𝛗̇6)(𝑥 − 6) нм
3
99106,56 − 149239,84𝑡 3 + 64221050,88𝑡 − 828𝑡 6 − 93312𝑡 4 + 108𝑡 9 − 186624𝑡 7
48833.28 (
) + 3𝑡 3 − 2
(49553,28 + 144𝑡 3 + 72𝑡 6 )2
𝑁𝑦 =
−2 − 2𝑡 3
𝑁𝑦1 = −492.46 н
Задание И5. Уравнений Лагранжа. Теорема об изменении кинетической энергии в
переносном движении
1.
Дифференциальные уравнения движения системы найдем из уравнений Лагранжа. За обобщенные
координаты выберем x и φ.
Запишем соответствующие уравнения Лагранжа:
𝑑 𝜕𝑇 𝜕𝑇
𝑑 𝜕𝑇 𝜕𝑇
−
= 𝑄𝑥 ;
−
= 𝑄𝜑 (5.1)
𝑑𝑡 𝜕𝑥̇ 𝜕𝑥
𝑑𝑡 𝜕𝜑̇ 𝜕𝜑
Выражение кинетической энергии системы (4.2) позаимствуем из задания И4
𝐽диск 2 𝑚 2
𝑚
𝑇 = 𝑇диск + 𝑇𝑀 =
𝜑̇ + 𝑣 = 24416.64𝜑̇ 2 + (𝑥̇ 2 + 𝜑̇ 2 (𝑅 2 + (𝑥 − 𝑅)2 ) + 2𝑥̇ 𝜑̇ 𝑅)(5.2)
2
2
2
Производные по 𝑥:
Обобщенная сила
𝑑 𝜕𝑇
= 𝑚(𝑥̈ + 𝜑̈ 𝑅);
𝑑𝑡 𝜕𝑥̇
𝜕𝑇
= 𝑚(𝑥 − 𝑅)𝜑̇ 2 ;
𝜕𝑥
(5.3)
𝑄𝑥 = 0 (5.4)
равна нулю, поскольку нет сил, имеющих составляющие вдоль 𝑥
Подставив (5.3) и (5.4) в (5.1) получаем дифференциальное уравнение по 𝑥:
𝑥̈ + 𝜑̈ 𝑅 = (𝑥 − 𝑅)𝜑̇ 2 (5.5)
Поскольку.
𝜕𝑇
= 0;
𝜕𝜑
𝑄𝜑 = 0 (5.6)
9
то 𝜑 является циклической координатой, и ей соответствует циклический интеграл
дифференциального уравнения по 𝜑:
𝜕𝑇
= 𝜑̇ (49589,28 + 18𝑥 2 − 216𝑥) + 108𝑥̇ = 𝑐𝑜𝑛𝑠𝑡 (5.7)
𝜕𝜑̇
Покажем, что циклический интеграл (5.7) выражает факт сохранение кинетического момента
системы относительно оси z. Согласно формуле (2.1) задания И2
𝐾𝑧 = (𝐽диск + 𝐽𝑚 )𝜑̇ + 𝑚𝑥̇ 𝑅
(5.8)
Подстановка значений дает
𝐾𝑧 = 𝜑̇ (49589,28 + 18𝑥 2 − 216𝑥) + 108𝑥̇
что в точности совпадает с выражением (5.7).
Значит (5.7) действительно выражает факт сохранение кинетического момента системы
относительно оси z. Ввиду начального покоя системы
𝐾𝑧 = 𝐶𝑜𝑛𝑠𝑡 = 0 (5.9)
Производная от (5.7) приводит к дифференциальному уравнению по 𝜑
𝜑̈ (49589,28 + 18𝑥 2 − 216𝑥) + 36𝑥̇ 𝜑̇ (𝑥 − 6) + 108𝑥̈ = 0
(5.10)
2. Проверим уравнение относительного движения точки (1.2) в условиях задачи А.
При подстановке условий задачи А: 𝜑̇ = −2 = 𝐶𝑜𝑛𝑠𝑡 в (5.5) получаем точно такое же
уравнение, как в задаче А
𝑥̈ − 4𝑥 = −24
(5.11)
3. Проверим закон угловой скорости тела, найденный в условиях задачи Б
При подстановке условий задачи Б при отсутствии момента 𝑀𝑧 = −3𝑡 3 + 2 в (5.7) получаем тот же
закон угловой скорости
(49553.28 + 144𝑡 3 + 72𝑡 6 )𝜑̇ − 648𝑡 2 = 𝐾𝑧 = 0 или 𝜑̇ =
что и в задании И2 при отсутствии момента.
4.
648𝑡 2
49553.28 + 144𝑡 3 + 72𝑡 6
(5.12)
Общее выражение зависимости реакции 𝑁𝑦 тела на точку найдем из теоремы об изменении
кинетической энергии точки в переносном движении
𝑇̇1 + 2𝑇̇0 −
𝜕𝑇
= 𝑵𝒚 ∙ 𝒗𝒆
𝜕𝑡
(5.13)
Здесь использовано разложение выражения кинетической энергии точки Т на слагаемые по степеням
относительной скорости. Справа стоит мощность внешних сил (они здесь состоят из одной реакции 𝑁𝑦 )
на
переносном движении точки.
𝑚
𝑇𝑀 = (𝑥̇ 2 + 𝜑̇ 2 (𝑅 2 + (𝑥 − 𝑅)2 ) + 2𝑥̇ 𝜑̇𝑅) = 𝑇2 + 𝑇1 + 𝑇0
(5.14)
2
Кинетическая энергия Т не содержит времени t, поэтому
𝜕𝑇
=0
(5.15)
𝜕𝑡
Энергия T1 , содержащая 𝑥̇ в первой степени и ее производная
𝑇1 = 𝑚𝑥̇ 𝜑̇𝑅
𝑇̇1 = 𝑅𝑚(𝑥̈ 𝜑̇ + 𝑥̇ 𝜑̈)
(5.16)
Энергия T0 , содержащая 𝑥̇ в нулевой степени и ее производная
𝜑̇2
(𝑥 2 − 2𝑅𝑥 + 2𝑅 2 )
2𝑇̇0 = 2𝑚𝜑̈ 𝜑̇ (𝑥 2
2
Мощность реакции в переносном движении точки
𝑇0 = m
− 2𝑅𝑥 + 2𝑅 2 ) + 2𝜑̇ 2 𝑥̇ 𝑚(𝑥 −R)
(5.17)
𝑵𝒚 ∙ 𝒗𝑒 = 𝑁𝒚 𝜑̇ (𝑥 − 𝑅)
(5.18)
После подстановки в теорему (5.13) получаем
𝑁𝒚 𝜑̇ (𝑥 − 𝑅) = 𝑅𝑚(𝑥̈ 𝜑̇ + 𝑥̇ 𝜑̈) + 2𝑚𝜑̈ 𝜑̇ (𝑥2 − 2𝑅𝑥 + 2𝑅2 ) + 2𝜑̇ 2 𝑥̇ 𝑚(𝑥 −R)
𝑅𝑚(𝑥̈ 𝜑̇ + 𝑥̇ 𝜑̈) + 2𝑚𝜑̈ 𝜑̇ (𝑥2 − 2𝑅𝑥 + 2𝑅2 )
𝑁𝒚 = 2𝑥̇ 𝜑𝑚
̇ +
𝜑̇ (𝑥 − 𝑅)
(5.19)
Проверим выражение (для реакции Ny в условиях задачи А, где: 𝜑̇ = −2 = 𝐶𝑜𝑛𝑠𝑡, 𝜑̈ = 0
Подставив эти условия в (5.19), получаем
10
216𝑥̈
2(𝑥 − 6)
В силу дифференциального уравнения движения точки
𝑥̈ − 4𝑥 = −24
получаем то же выражение (1.8)
𝑁𝑦 = −72𝑥̇ + 432
что и в задании И1.
𝑁𝑦 = −72𝑥̇ +
Ответ задачи В
2
1
𝑥̈ + 𝜑̈ 𝑅 − (𝑥 − 𝑅)𝜑̇ 2 = 0
𝜑̈ (49589,28 + 18𝑥 2 − 216𝑥) + 36𝑥̇ 𝜑̇ (𝑥 − 6) + 108𝑥̈ = 0
3
4
2
𝜑̇ =
𝑥̈ − 4𝑥 = −24
648𝑡
49553.28 + 144𝑡 3 + 72𝑡 6
216𝑥̈
2(𝑥 − 6)
𝑁𝑦 = −72𝑥̇ + 432
𝑁𝑦 = −72𝑥̇ +