R(м)

Индивидуальное задание 1
m
(кг)
R(м)
𝛼
(град)
𝛾
(кг/м2)
𝛗̇ (c-1)
x0
(м)
𝐱̇ 𝟎
(м/с)
17
10
45
8
-2
1
-4
𝐌𝐳 (нм)
-𝟒𝐭 𝟑 − 𝟒
𝐱(𝐭) (м)
𝟑 − 𝟐𝐭 𝟐
mg
Ny,Фc
g g
g ω
y
𝑣𝑟 ,Фе
g z
x
// //
r
, , R1
R
α
R1
е
α
z
𝑊𝑒
//
z
g
,
z
O
R1с
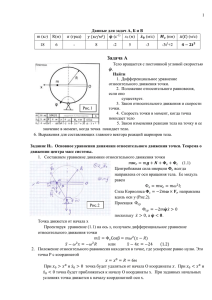
1. Составляем
уравнение динамики относительного движения точки
ω
z
𝑚𝒘𝒓 = 𝑚𝒈 + 𝑵 + 𝚽е + 𝚽с
(1.1)
Центробежная
сила инерции 𝚽е всегда Фе направлена от оси вращения
//
тела.
, Ее модуль равен
Фе = 𝑚𝑤𝑒 = 𝑚𝜔2 ℎ = 𝑚𝜔2 𝑥;
Сила Кориолиса 𝚽с = −2𝛚 × 𝑽𝒓 направлена вдоль оси у (Рис.2).
Проекция Фс𝑦
Фс𝑦 = −2𝑚𝛗̇ 𝑥̇ < 0
поскольку 𝑥̇ < 0, а 𝛗̇ < 𝟎.
Проектируя
уравнение (1.1) на ось х, получаем дифференциальное
уравнение относительного движения точки
𝑚𝑥̈ = Феx = 𝑚𝜔2 𝑥
𝑥̈ = 𝜔2 𝑥
или
𝑥̈ − 16𝑥 = 0
(1.2)
2) Положение относительного равновесия находится в точке, где ускорение
равно нулю. Это точка Р с координатой
𝑥̈ − 16𝑥 = 0
𝑥̈ = 0
16𝑥 = 0
𝑥 = 𝑥0 = 0 м
Очевидно, что при 𝑥0 > 𝑥 0 и 𝑥̇ 0 > 0 точка будет удаляться от начала О
координаты 𝑥. При заданных начальных условиях точка движется в
направлении оси х.
3) Найдем закон относительного движения и скорости точки. Это обратная
задача динамики. Решение однородного уравнения (1.1) ищем в виде
𝑥 = 𝑥𝑜𝑜
Решение однородного уравнения 𝑥𝑜𝑜 ищем в виде
𝑥𝑜𝑜 = 𝑒 𝜆𝑡 ;
Подставляя
решение
в
однородное
уравнение,
приходим
характеристическому уравнению с вещественными корнями
𝜆2 − 𝜔2 = 0;
𝜆1,2 = ±𝜔;
Решение принимает вид
𝑥𝑜𝑜 = 𝐶1 𝑒 𝜔𝑡 + 𝐶2 𝑒 −𝜔𝑡
Полное решение уравнения (1.1)
𝑥 = 𝐶1 𝑒 𝜔𝑡 + 𝐶2 𝑒 −𝜔𝑡 ;
𝑥̇ = 𝜔𝐶1 𝑒 𝜔𝑡 − 𝜔𝐶2 𝑒 −𝜔𝑡 (1.3)
Постоянные 𝐶1 𝐶2 в (1.3) находим из начальных условий
𝑡 = 0: 𝑥0 = 1 м;
𝑥̇ 0 = 4 м/с
(1.4)
Подставив (1.4) в (1.3), получим:
𝑥0 = 𝐶1 + 𝐶2 ;
𝑥̇ 0 = 𝜔(𝐶1 − 𝐶2 )
к
Иначе
𝑥̇ 0
𝑥̇ 0
+ 𝐶2 = 𝐶1 𝑥0 = + 2𝐶2 ;
𝜔
𝜔
𝑥̇ 0
𝑥̇ 0
𝑥̇ 0
𝐶2 = 𝐶1 −
𝑥0 = + 2𝐶2 = 2𝐶1 −
;
𝜔
𝜔
𝜔
𝑥̇ 0
𝑥̇ 0
2𝐶2 = 𝑥0 −
;
2𝐶1 = 𝑥0 +
𝜔
𝜔
Решение приобретает вид
1
𝑥̇ 0 1 𝜔𝑡
𝑥̇ 0
(𝑒 − 𝑒 −𝜔𝑡 ) = 𝑥0 𝑐ℎ𝜔𝑡 + 𝑠ℎ𝜔𝑡
𝑥 = 𝑥0 (𝑒 𝜔𝑡 + 𝑒 −𝜔𝑡 ) +
2
𝜔2
𝜔
С учетом начальных условий (1.4)
𝑥 = 𝑐ℎ(2𝑡) − 2𝑠ℎ(2𝑡);
𝑥̇ = 2𝑠ℎ(2𝑡) − 4𝑐ℎ(2𝑡) (1.5)
1. Найдем скорость точки в момент, когда она покидает тело. Можно было бы и
закона движения определить соответствующий момент времени и подставить его в
закон изменения скорости. Но проще найти зависимость скорости точки от ее
перемещения известной заменой
𝑑𝑥̇
𝑑𝑥
Которая фактически приводит к теореме об изменении кинетической
𝑥̈ = 𝑥̇
энергии точки.
Получаем
𝑑𝑥̇
= 𝜔2 𝑥; или 𝑥̇ 𝑑𝑥̇ = 𝜔2 𝑥𝑑𝑥
𝑑𝑥
Интегрируя, находим зависимость относительной скорости точки от ее
𝑥̇
перемещения
𝑥̇ 2 = 𝜔2 𝑥 2 + 𝐶3
(1.6)
Из начальных условий (1.4) находим
2
𝐶3 = 𝑥̇ 0 2 − 𝜔2 𝑥0 = 16 − 4 = 12 м2 /с2
Находим скорость при 𝑥1 = 𝑅21/2 = 14м
𝑥̇ 1 = √16 ∗ 196 + 12 = 56 м/с
5) Найдем закон изменения реакции тела на точку.
динамики. Проекция уравнения (1.1) на ось z:
0 = 𝑁𝑧 − 𝑚𝑔;
Это прямая задача
дает проекцию реакции стержня на ось z
𝑁𝑧 = 𝑚𝑔
(1.7)
Проектируя уравнение (1.1) на ось у, находим:
0 = 𝑁𝑦 + Фсy ;
Теперь проекция нормальной реакции стержня на ось у равна
𝑁𝑦 = 2𝑚𝛗̇ 𝑥̇ = 136𝑥̇ н (1.8)
𝑁𝑦 зависит от найденной относительной скорости точки (1.5).
В момент, когда точка покидает тело
𝑁𝑧 = 𝑚𝑔 = 170 н;
𝑁𝑦 = −2𝑚𝛗̇ 𝑥̇ 1 |𝑥=𝑥1 = 7616 н
(1.9)
6) Составляющие реакции шарнира R найдем по известным ускорениям
тела и точки из теоремы о движении центра масс
𝑹 = 𝑀𝒘𝒄
Это прямая задача динамики.
z
ω
ω
//
z
,
x
//
R1 r
,
R1е
R2
R
R1с
O
𝑀𝒘𝒄 = 𝑚𝒘 + 𝑀2 𝒘𝒄2 = 𝑹𝟏 + 𝑹𝟐
где
𝑹𝟏 составляющая
от
ускорения
точки.
Она
относительного, переносного и Кориолисова ускорений:
𝑹𝟏 = 𝑹1𝑟 + 𝑹1𝑒 + 𝑹1𝑐 = 𝑚𝒘𝑟 + 𝑚𝒘𝑒 + 𝑚𝒘𝑐
состоит
из
Направления составляющих изобразим на рисунке и вычислим их
величину
𝑅2 = 𝜋𝑅2 γ𝜔2 𝑅= 𝜋γ𝜔2 𝑅3
𝑅1𝑒 = 𝑚𝜔2 𝑅21/2
𝑅1𝑟 = 𝑚𝑥̈ = 𝑚ω2 (x − 𝑅21/2 )
𝑅1𝑐 = 𝑚𝑤𝑐 = 2𝑚𝜔𝑣1
(1.10)
Индивидуальное задание 2
m
(кг)
R(м)
𝛼
(град)
𝛾
(кг/м2)
𝐌𝐳 (нм)
𝐱(𝐭) (м)
17
10
45
8
-𝟒𝐭 𝟑 − 𝟒
𝟑 − 𝟐𝐭 𝟐
z
mg
y
x
R
α
𝑋0
O
1. Найдем закон изменения угловой скорости тела из теоремы об изменении
кинетического момента относительно оси вращения тела.
Кинетический момент системы складывается из кинетического момента
стержней АОВ с зафиксированной на них в текущий момент точкой.
𝐾𝑧 = (𝐽п + 𝐽𝑚 )𝜑̇
(2.1)
Моменты инерции пластины равен:
𝑚пл 𝑅2
3
𝐽пл =
+ 𝑚пл 𝑅2 = 𝛾𝜋𝑅4 = 3.77 ∗ 105 (2.2)
2
2
Момент инерции точки в текущем положении
𝐽𝑚 = 𝑚𝑥 2 = 𝑚(3 − 2𝑡 2 )2 = 𝐦(𝟗 − 𝟏𝟐𝐭 𝟐 + 𝟒𝐭 𝟒 )
= 𝟏𝟓𝟑 − 𝟐𝟎𝟒𝐭 𝟐 + 𝟔𝟖𝐭 𝟒 кгм2 ;
Итак
𝐽 = 𝐽пл + 𝐽𝑚 = 3.771 ∗ 105 − 204𝑡 2 + 68𝑡 4 кгм2
(2.3)
Кинетический момент системы равен:
𝐾𝑧 = (3.771 ∗ 105 − 204𝑡 2 + 68𝑡 4 )𝜑̇
(2.4)
Интегрируем теорему об изменении кинетического момента
𝐾𝑧̇ = 𝑀𝑧 = 𝟒𝐭𝟑 − 𝟒;
Получаем
𝐾𝑧 = 𝑡 4 − 4𝑡
(2.5)
Иначе
(3.771 ∗ 105 − 204𝑡 2 + 68𝑡 4 )𝜑̇ = 𝑡 4 − 4𝑡
Отсюда находим закон угловой скорости тела
𝜑̇ =
𝑡 4 − 4𝑡
(3.771 ∗ 105 − 204𝑡 2 + 68𝑡 4 )
(2.6)
В момент, когда точка покидает тело.
𝑥1 = 𝟑 − 𝟐𝐭 𝟐 = 0; 𝑡1 = √1.5 = 1.225 𝑐,
𝜑̇ 1 = −7.029 ∗ 10−6 с−1
(2.7)
2. Найдем закон изменения движущей силы сцепления 𝑭сц , которая создается
мотором экипажа и обеспечивает заданное движение точки по телу. С
учетом силы 𝑭сц дифференциальное уравнение относительного движения
точки (1.2) приобретает вид
𝑚𝑥̈ = 𝑚𝜔2 𝑥 + 𝐹𝑐ц𝑥
Отсюда находим закон изменения силы
(2.8)
(𝑡 4 − 4𝑡)2 (3 − 2𝑡 2 )
𝐹𝑐ц (𝑡) = 𝑚𝑥̈ − 𝑚𝜔 𝑥 = 17 (−4 −
)
(3.771 ∗ 105 − 204𝑡 2 + 68𝑡 4 )2
2
(2.9)
3. Силу реакции 𝑁𝑦 точки на тело найдем из дифференциального уравнения
вращения тела. 𝐽пл 𝜑̈ = 𝑀𝑧 + 𝑁𝑦 𝑥
(2.10)
Или
𝐽пл 𝜑̈ = −𝟒𝐭𝟑 − 𝟒 + 𝑁𝑦 𝑥
(2.11)
Отсюда
𝐽пл 𝜑̈ + 𝟒𝐭𝟑 + 𝟒
𝑁𝑦 =
𝑥
(2.12)
Дифференцируя закон угловой скорости 𝜑̇ , получаем:
𝜑̈
(4𝑡 3 − 4)(3.771 ∗ 105 − 204𝑡 2 + 68𝑡 4 ) + (408𝑡 − 272𝑡 3 )(𝑡 4 − 4𝑡)
=
(3.771 ∗ 105 − 204𝑡 2 + 68𝑡 4 )2
(2.13)
В момент вылета точки 𝑡1 = √3 𝑐
𝜑1̈ = 6.5 ∗ 10−6
𝑁𝑦1 =
3.77∗105 ∗6.5∗10−6 +4∗1,2253 +4
3−2∗1,2252
(2.14)
= −11040 Н (2.15)
4. В задаче А тело вращается равномерно, значит сумма моментов всех сил,
действующих на тело, равна нулю. На тело, кроме момента 𝑀𝑧 , действует
сила давления, обратная по направлению силе 𝑁𝑦 , найденной в задаче А
𝑁𝑦 = 2𝑚𝛗̇ 𝑥̇
Ее момент относительно оси z равен
𝑁𝑦 𝑥
Приравнивая сумму моментов нулю
𝑀𝑧 − 𝑁𝑦 𝑥 = 0
(2.16)
находим
закон изменения вращательного момента, поддерживающий
постоянную угловую скорость тела
𝑀𝑧 = 𝑁𝑦 𝑥 = 2𝑚𝛗̇ 𝑥̇ 𝑥 = −68𝑥̇ 𝑥 нм (2.17)
где законы относительного движения 𝑥 и скорости точки 𝑥̇ являются
известными функциями времени (1.5)
Индивидуальное задание №3
m
(кг)
R(м)
𝛼
(град)
𝛾
(кг/м2)
𝛗̇ (c-1)
x0
(м)
𝐱̇ 𝟎
(м/с)
17
10
45
8
-2
1
-4
𝟑 − 𝟐𝐭 𝟐
g g
g ω
y
𝑣𝑟 ,Фе
g z
x
// //
r
, , R1
h
R
-𝟒𝐭 𝟑 − 𝟒
𝐱(𝐭) (м)
Не было рисунка
mg
Ny,Фc
𝐌𝐳 (нм)
α
R1
е
R1с
1.
Найдем
дифференциальное
уравнение
относительного движения
точки из уравнения
Лагранжа
α
𝑊𝑒
//
g
,
ω
𝑑 𝜕𝑇 𝜕𝑇
−
= 𝑄𝑥 ,
𝑑𝑡 𝜕𝑥̇ 𝜕𝑥
(3.1)
𝑇=
𝑚 2
𝑉
2
z
Абсолютная
скорость V точки складывается из переносной и относительной
//
скоростей
(Рис.2)
,
𝑉 2 = 𝑥̇ 2 + 𝑣𝑒 2 ,
𝑣𝑒 = 𝜔ℎ, ℎ = 𝑥;
(3.2)
Таким образом, кинетическая энергия приобретает выражение
𝑚
𝑇 = (𝑥̇ 2 + 𝜔2 𝑥 2 )
(3.3)
2
Находим производные:
𝜕𝑇
= 𝑚𝑥̇ ;
𝜕𝑥̇
𝑑 𝜕𝑇
= 𝑚𝑥̈ ;
𝑑𝑡 𝜕𝑥̇
𝜕𝑇
= 𝑚𝜔2 𝑥;
𝜕𝑥
Обобщенная сила 𝑄𝑥 = 0 поскольку сила тяжести перпендикулярна скорости
точки и не имеет мощности.
Подставив
производные
в
уравнение
Лагранжа
приходим
к
дифференциальному уравнению (1.2), найденному в И1
𝑥̈ − 𝜔2 𝑥 = 0
(3.4)
𝑥̈ = 𝜔2 𝑥 (1.2) (из И1)
2. Реакцию 𝑁𝑦 тела на точку найдем из теоремы об изменении
кинетической энергии точки.
𝑇̇ = 𝑁
где N- мощность физических сил, приложенных к точке, в переносном и в
относительном движениях точки.
𝑁 = 𝑁𝜑 + 𝑁𝑥
Физических сил, имеющих проекцию на ось 𝑥 нет, поэтому
𝑁𝑥 = 𝑄𝑥 𝑥̇ = 0
Во вращательном переносном движении точки мощность реакции вычисляем
через момент
𝑁𝜑 = 𝑚𝑧 (𝑵𝑦 )𝜑̇ ;
В соответствии с Рис.2
𝑇̇ =
𝜕𝑇
𝜕𝑇
𝑥̈ +
𝑥̇ = 𝑚𝑥̇ 𝑥̈ + 𝑚𝜔2 𝑥𝑥̇ = 𝑁𝒚 𝜔𝑥
𝜕𝑥̇
𝜕𝑥
Из дифференциального уравнения (3.4)
𝑥̈ = 𝜔2 𝑥
Таким образом, после сокращения на 𝜔𝑥 находим тот же результат,
что и в И1
𝑁𝑦 = 𝑚𝜔𝑥̇ + 𝑚𝜔𝑥̇ = 2𝑚𝜑̇ 𝑥̇ = 136𝑥̇ н
(3.5)
Задание И4. Уравнения Лагранжа.
m
(кг)
R(м)
𝛼
(град)
𝛾
(кг/м2)
Mz (нм)
x(t) (м)
17
10
45
8
4t 3 − 4
3 − 2t 2
z
mg
y
x
R
α
𝑋0
O
1. Найдем закон изменения угловой скорости из уравнения Лагранжа
𝑑 𝜕𝑇 𝜕𝑇
−
= 𝑄𝜑
𝑑𝑡 𝜕𝜑̇ 𝜕𝜑
(4.1)
Кинетическая энергия системы складывается из энергии тела и точки
𝑇 = 𝑇пл + 𝑇𝑀 =
𝐽пл 2 𝑚 2 3
𝑚
𝜑̇ + 𝑣 = 𝛾𝜋𝑅4 𝜑̇ 2 + (𝑥̇ 2 + 𝜑̇ 2 𝑥 2 )
2
2
4
2
(4.2)
Подставив данные задачи, находим
𝑇 = 188500𝜑̇ 2 +
17
{16𝑡 2 + 𝜑̇ 2 (9 − 12𝑡 2 + 4𝑡 4 )} (4.3)
2
Обобщенная сила 𝑄𝜑 = 𝑀𝑧 = −4t 3 − 4
𝜕𝑇
= 0,
𝜕𝜑
(4.4)
𝜕𝑇
= 3.77 ∗ 105 𝜑̇ + 17𝜑̇ (9 − 12𝑡 2 + 4𝑡 4 ) = 𝑡 4 − 4𝑡,
𝜕𝜑̇
Приходим к тому же результату, что и в И2:
𝑡 4 − 4𝑡
𝜑̇ =
;
3.771 ∗ 105 − 204𝑡 2 + 68𝑡 4
𝜑̇ 1 = −1.055 ∗ 10−5 с−1 (4.5)
Видим, что в данном примере кинетический момент системы связан с
кинетической энергией формулой
𝜕𝑇
= 𝐾𝑧
𝜕𝜑̇
(4.6)
Задание И5. Уравнений Лагранжа. Теорема об изменении кинетической
энергии в переносном движении
z
mg
y
x
R
α
𝑋0
O
m
(кг)
R(м)
𝛼
(град)
𝛾
(кг/м2)
𝐌𝐳 (нм)
𝐱(𝐭) (м)
17
10
45
8
-𝟒𝐭 𝟑 − 𝟒
𝟑 − 𝟐𝐭 𝟐
1. Дифференциальные уравнения движения системы найдем
из уравнений Лагранжа. За обобщенные координаты
выберем x и φ.
Запишем соответствующие уравнения Лагранжа:
𝑑 𝜕𝑇 𝜕𝑇
𝑑 𝜕𝑇 𝜕𝑇
−
= 𝑄𝑥 ;
−
= 𝑄𝜑 (5.1)
𝑑𝑡 𝜕𝑥̇ 𝜕𝑥
𝑑𝑡 𝜕𝜑̇ 𝜕𝜑
Выражение кинетической энергии системы (4.2) позаимствуем из задания И4
𝑇 = 𝑇пл + 𝑇𝑀 =
𝐽пл 2 𝑚 2 3
𝑚
𝜑̇ + 𝑣 = 𝛾𝜋𝑅4 𝜑̇ 2 + (𝑥̇ 2 + 𝜑̇ 2 𝑥 2 ) (5.2)
2
2
4
2
Производные по 𝒙:
𝑑 𝜕𝑇
= 𝑚𝑥̈ ;
𝑑𝑡 𝜕𝑥̇
Обобщенная сила
𝜕𝑇
= 𝑚𝜑̇ 2 𝑥;
𝜕𝑥
(5.3)
𝑄𝑥 = 0 (5.4)
равна нулю, поскольку нет сил, имеющих составляющие вдоль 𝑥
Подставив (5.3) и (5.4) в (5.1) получаем дифференциальное уравнение
по 𝑥:
𝑚𝑥̈ = 𝑚𝜑̇ 2 𝑥 (5.5)
Поскольку.
𝜕𝑇
= 0;
𝑄𝜑 = 0
(5.6)
𝜕𝜑
то 𝜑 является циклической координатой, и ей соответствует циклический
интеграл дифференциального уравнения по 𝜑:
𝜕𝑇 3
= 𝛾𝜋𝑅4 𝜑̇ + 𝑚𝜑̇ 𝑥 2 = 𝐶𝑜𝑛𝑠𝑡
(5.7)
𝜕𝜑̇ 2
Покажем, что циклический интеграл (5.7) выражает факт сохранение
кинетического момента системы относительно оси z. Согласно формуле (2.1)
задания И2
𝐾𝑧 = (𝐽п + 𝐽𝑚 )𝜑̇
Подстановка данных задачи дает
3
𝐾𝑧 = ( 𝛾𝜋𝑅4 + 𝑚𝑥 2 )𝜑̇
(5.8)
2
что в точности совпадает с выражением (5.7).
Значит (5.7) действительно выражает факт сохранение кинетического
момента системы относительно оси z. Ввиду начального покоя системы
𝐾𝑧 = 𝐶𝑜𝑛𝑠𝑡 = 0 (5.9)
Производная от (5.7) приводит к дифференциальному уравнению по 𝜑
3
𝜑̈ ( 𝛾𝜋𝑅4 + 𝑚𝑥 2 ) = 0
(5.10)
2
2. Проверим уравнение относительного движения точки (1.2) в
условиях задачи А.
При подстановке условий задачи А: 𝜑̇ = −4 = 𝐶𝑜𝑛𝑠𝑡 в (5.5) получаем точно
такое же уравнение, как в задаче А
ẍ − 16x = 0
(5.11)
3. Проверим закон угловой скорости тела, найденный в условиях
задачи Б
При подстановке условий задачи Б при отсутствии момента 𝑀𝑧 : 𝑥 = 𝟑 − 𝟐𝐭 𝟐
в (5.7) получаем тот же закон угловой скорости
3
( 𝛾𝜋𝑅4 + 𝑚(3 − 2𝑡 2 )2 )𝜑̇ = 𝐾𝑧 = 0 или 𝜑̇ = 0 (5.12)
2
что и в задании И2 при отсутствии момента.
4. Общее выражение зависимости реакции 𝑁𝑦 тела на точку
найдем из теоремы об изменении кинетической энергии
точки в переносном движении
𝜕𝑇
𝑇1̇ + 2𝑇̇0 −
= 𝑵𝒚 ∙ 𝒗𝑒 (5.13)
𝜕𝑡
Здесь использовано разложение выражения кинетической энергии
точки Т на слагаемые по степеням относительной скорости. Справа
стоит мощность внешних сил (они здесь состоят из одной реакции
𝑁𝒚 ) на переносном движении точки.
𝑚 2
(𝑥̇ + 𝜑̇ 2 𝑥 2 ) = 𝑇1 + 𝑇0
𝑇𝑀 =
(5.14)
2
Кинетическая энергия Т не содержит времени t, поэтому
𝜕𝑇
=0
(5.15)
𝜕𝑡
Энергия T1 , содержащая 𝑥̇ в первой степени и ее производная
𝑇1 = 0
𝑇1̇ = 0
(5.16)
Энергия T0 , содержащая 𝑥̇ в нулевой степени и ее производная
𝑚
𝑇0 = 𝜑̇ 2 𝑥 2
2𝑇̇0 = 2𝑚𝜑̇ 2 𝑥̇ 𝑥
(5.17)
2
Мощность реакции в переносном движении точки
𝑵𝒚 ∙ 𝒗𝑒 = 𝑁𝒚 𝜑̇ 𝑥
(5.18)
После подстановки в теорему (5.13) получаем
𝑁𝒚 𝜑̇ 𝑥 = 2𝑚𝜑̇ 2 𝑥̇ 𝑥
𝑁𝒚 = 2𝑚𝛗̇𝑥̇ (5.19)
Проверим выражение (для реакции Ny в условиях задачи А, где: 𝜑̇ = −4 =
= 𝐶𝑜𝑛𝑠𝑡
Подставив эти условия в (5.19), получаем
𝑁𝑦 = 136𝑥̇
то же выражение (1.8), что и в задании И1.