Приложение №1
реклама

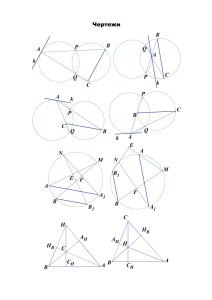
Приложение №1 1. Две окружности касаются внешним образом в точке A. Прямая l касается первой окружности в точке B, а второй - в точке C. a) Докажите, что треугольник ABC прямоугольный. b) Найдите площадь треугольника ABC, если радиусы окружностей 8 и 2. 2. Окружность проходит через вершину C прямоугольника ABCD, касается стороны AB, пересекает сторону CD в точке M и касается стороны AD в точке K. a) Докажите, что угол CKD равен углу KMD. b) Найдите сторону AB, зная, что AD = 18, DM = 4. 3. Окружности 𝜔1 с центром O1 и окружность 𝜔2 с центром O2 касаются внешним образом. Из точки O1 к 𝜔2 проведена касательная O1A, а из точки O2 к 𝜔1 проведена касательная O2B (A и B – точки касания). a) Докажите, что углы O1AB и O1O2B равны. b) Найдите площадь четырехугольника O1O2AB, если известно, что точки A и B лежат по одну сторону от прямой O1O2, а радиусы окружностей равны соответственно 2 и 3. 4. На диаметре AB окружности 𝜔 выбрана точка C. На отрезках AC и BC как на диаметрах построены окружности 𝜔1 и 𝜔2 соответственно. Прямая l пересекает окружность 𝜔 в точках A и D, окружность 𝜔1 в точках A и E, а окружность 𝜔2 - в точках M и N. a) Докажите, что MD=NE. b) Найдите радиус круга, касающегося окружностей 𝜔, 𝜔1 и 𝜔2 , если известно, что AC = 10, BC = 6. 5. Окружность касается стороны AB параллелограмма ABCD, пересекает стороны AD и BC в точках M и N соответственно и проходит через вершины C и D. a) Докажите, что DN = CM. b) Найдите DN, зная, что AM = 9, BN = 16, BC = 18. 6. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K. a) Докажите, что отрезок BK больше отрезка CK. b) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB , если BK = 18 и BN = 17.