1)Формулы сокращенного умножения. 1) Квадрат суммы двух
реклама
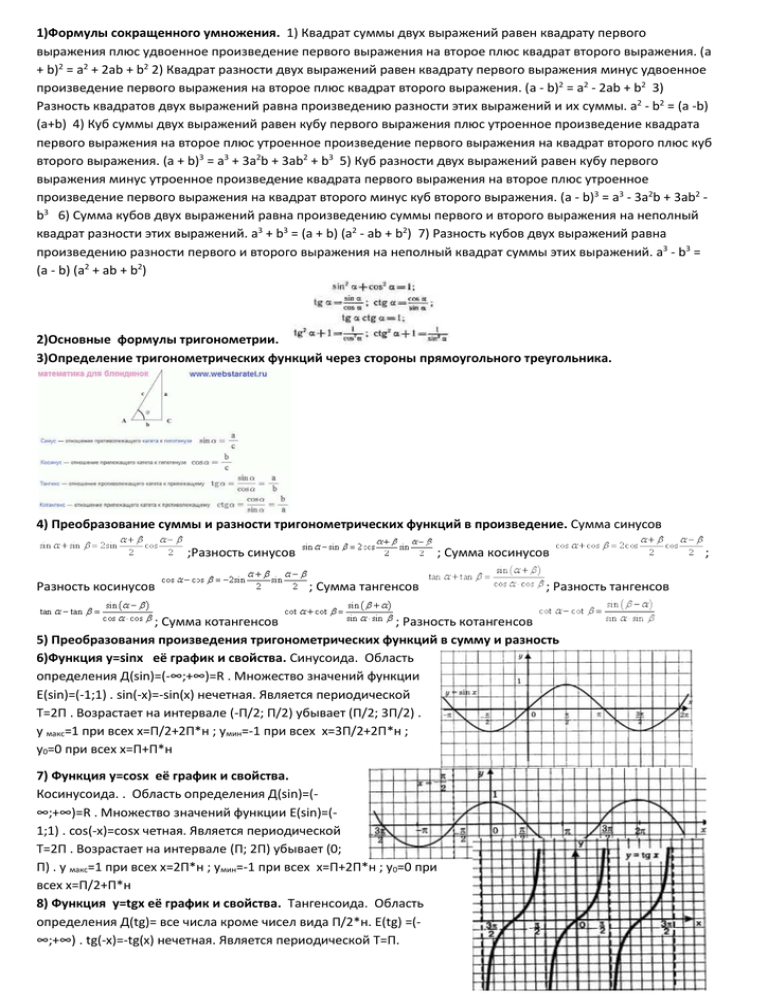
1)Формулы сокращенного умножения. 1) Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения. (a + b)2 = a2 + 2ab + b2 2) Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения. (a - b)2 = a2 - 2ab + b2 3) Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. a2 - b2 = (a -b) (a+b) 4) Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. (a + b)3 = a3 + 3a2b + 3ab2 + b3 5) Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. (a - b)3 = a3 - 3a2b + 3ab2 b3 6) Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений. a3 + b3 = (a + b) (a2 - ab + b2) 7) Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений. a3 - b3 = (a - b) (a2 + ab + b2) 2)Основные формулы тригонометрии. 3)Определение тригонометрических функций через стороны прямоугольного треугольника. 4) Преобразование суммы и разности тригонометрических функций в произведение. Сумма синусов ;Разность синусов Разность косинусов ; Сумма косинусов ; Сумма тангенсов ; Разность тангенсов ; Сумма котангенсов ; Разность котангенсов 5) Преобразования произведения тригонометрических функций в сумму и разность 6)Функция y=sinx её график и свойства. Синусоида. Область определения Д(sin)=(-∞;+∞)=R . Множество значений функции Е(sin)=(-1;1) . sin(-x)=-sin(x) нечетная. Является периодической Т=2П . Возрастает на интервале (-П/2; П/2) убывает (П/2; 3П/2) . у макс=1 при всех х=П/2+2П*н ; умин=-1 при всех х=3П/2+2П*н ; у0=0 при всех х=П+П*н 7) Функция у=cosx её график и свойства. Косинусоида. . Область определения Д(sin)=(∞;+∞)=R . Множество значений функции Е(sin)=(1;1) . cos(-x)=cosx четная. Является периодической Т=2П . Возрастает на интервале (П; 2П) убывает (0; П) . у макс=1 при всех х=2П*н ; умин=-1 при всех х=П+2П*н ; у0=0 при всех х=П/2+П*н 8) Функция у=tgx её график и свойства. Тангенсоида. Область определения Д(tg)= все числа кроме чисел вида П/2*н. Е(tg) =(∞;+∞) . tg(-x)=-tg(x) нечетная. Является периодической Т=П. ; Возрастает на всей области определения (-П/2+П*н; П/2+П*н). Не убывает. Умакс-нет . умин-нет . у0=0 при х = П*н . Положительное значение (П*н;П/2+П*н) . Отрицательное значение (-П/2+П*н; П*н) 9) Функция y=ctgx её график и свойства. Котангенсоида. Область определения Д(tg)= все числа кроме чисел вида П*н. Е(сtg) =(-∞;+∞) . сtg(-x)= -сtg(x) нечетная. Является периодической Т=П. Убывает на всей области определения (П*н; П+П*н). Не возрастает. Умакс-нет . умин-нет . у0=0 при х =П/2+ П*н . Положительное значение (П*н; П/2+П*н) . Отрицательное значение (-П/2+П*н; П*н) 10)Определение обратной функции arcsinA .Примеры. Арксинусом числа «а» называют такой угол принадлежащий интервалу от –П/2 до П/2 синус которого равен числу «а» 𝜋 𝜋 arcsin= φ 𝜑𝜖 [− ; ] sin φ=a. arcsin1=П/2 sinП/2=1; arcsin-1=-П/2 sin-П/2=-1 2 2 11) Определение обратной функции arccosA.Примеры. Арккосинусом числа «а» называют такой угол принадлежащий интервалу от 0 до П косинус которого равен числу «а». arccosа= φ φϵ[0;π] cos φ=a. Arccos1=0 cos0=1; arccos1/2=П/3 cosП /3=1/2; arccos-1/2=2П/3 cos2П /3=-1/2; 12) Определение обратной функции arctgA.Примеры. Арктангенсом числа «а» называют такой угол принадлежащий интервалу от от –П/2 до П/2 тангенс которого равен числу «а». arctga= φ φϵ(-π/2;π/2) tg φ=a. Arctg0=0 tg0=0; arctg1=П/4 tgП/4=1 ; arctg-1=-П/4 tg-П/4=-1 13) Определение обратной функции arcctgA.Примеры. Арккотангенсом числа «а» называют такой угол принадлежащий интервалу от от 0 до П котангенс которого равен числу «а» . arcctgа= φ φϵ(0;π) ctg φ=a . arcctg0=П/2 ctgП/2=0; arcctg1=П/4 ctgП/4=1; arcctg-1=3П/4 ctg3П/4=-1 14)Решение простейшего тригонометрического уравнения вида sinx=a. Уравнение sinx=a имеет бесчисленное количество решений если -1≤а≤1 . 𝑥 = (−1)𝑛 ∗ 𝑎𝑟𝑐𝑠𝑖𝑛𝑎 + 𝜋 ∗ 𝑛 . sinx=-1 x=-П/2+2П*n. Sinx=0 x=П*n. sinx=1 x=П/2+2П*n. 15) Решение простейшего тригонометрического уравнения вида cosx=a. Уравнение cosx=a имеет бесчисленное количество решений если -1≤а≤1. 𝑥 = ±𝑎𝑟𝑐𝑐𝑜𝑠𝑎 + 2𝜋 ∗ 𝑛. Cosx=-1 x=П+2П*n. Cosx=0 х=П/2+П*n. Cosx=1 x=2П*n. 16) Решение простейшего тригонометрического уравнения вида tgx=a. tgx=a x=arctga + П*n ; tgx=0; x=П*n 17) Решение простейшего тригонометрического уравнения вида ctgx=a. сtgx=a x=arcсtga + П*n ; ctg=-1 x=3П/4+П*n; ctgx=1 x=-П/2+П*n 18)Способы решения сложных уравнений. Решить уравнение вида 2cos2x+3cosx-2=0 cosx=t 2t2+3t-2=0 D=25 t1=1/2 t2=-2 cosx=1/2 x=±arccos1/2+2П*n x=±П/3+2П*n x=±60°+360°n cos=-2 -2‹-1 19) Решить уравнение вида cosx+cos2x+cos3x=0 20)Определение производной функции. Производные элементарных функций. Правила вычисления производных.





