Ф. И. Группа Дата Карта занятия по медицинской статистике №2
реклама
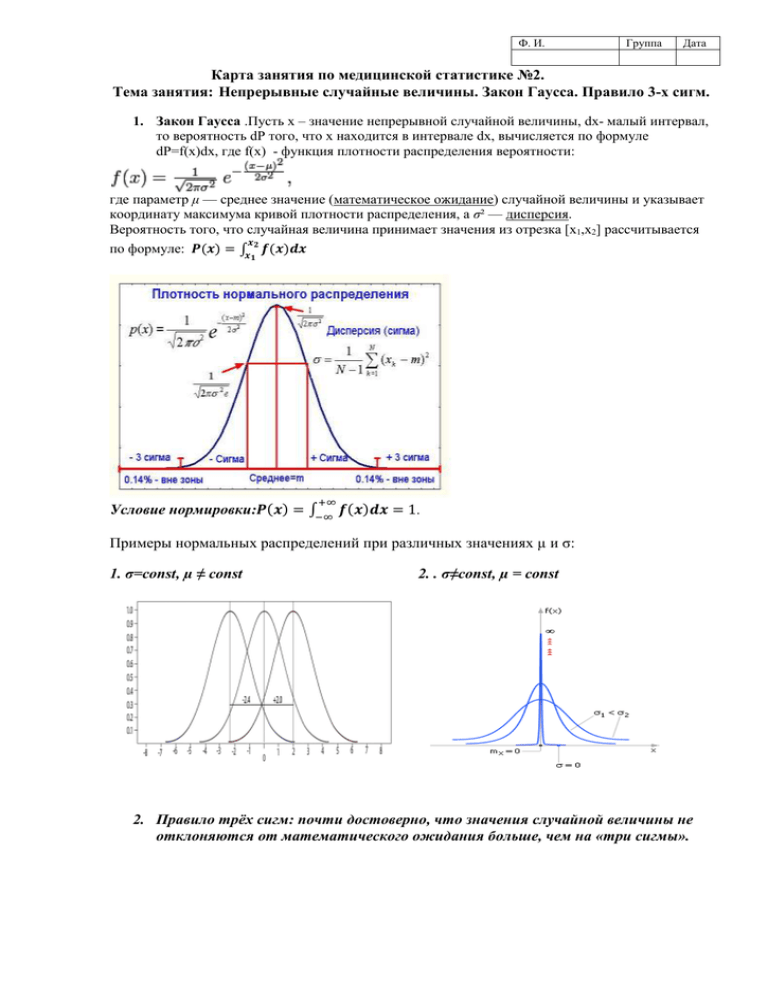
Ф. И. Группа Дата Карта занятия по медицинской статистике №2. Тема занятия: Непрерывные случайные величины. Закон Гаусса. Правило 3-х сигм. 1. Закон Гаусса .Пусть х – значение непрерывной случайной величины, dx- малый интервал, то вероятность dP того, что х находится в интервале dx, вычисляется по формуле dP=f(x)dx, где f(x) - функция плотности распределения вероятности: где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия. Вероятность того, что случайная величина принимает значения из отрезка [x1,x2] рассчитывается 𝒙 по формуле: 𝑷(𝒙) = ∫𝒙 𝟐 𝒇(𝒙)𝒅𝒙 𝟏 +∞ Условие нормировки:𝑷(𝒙) = ∫−∞ 𝒇(𝒙)𝒅𝒙 = 1. Примеры нормальных распределений при различных значениях µ и σ: 1. σ=const, µ ≠ const 2. . σ≠const, µ = const 2. Правило трёх сигм: почти достоверно, что значения случайной величины не отклоняются от математического ожидания больше, чем на «три сигмы». 3. Решение задач: 1) Нарисуйте кривые Гаусса для а) одинаковых µ и разных σ: µ=10, σ1 = 1, σ2= 3 и в) для различных µ и одинаковых σ:σ= 2, µ1= 4, µ2 =8. 2) Покажите на графике, чему равна вероятность того, что случайная непрерывная величина принимает значения из интервала 1 до 2. Запишите интеграл для расчета этой величины 3) Смоделируйте графики нормальных распределений суточных температур у здорового человека и больного ОРВИ:









