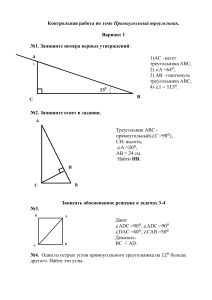
Задачи. 1. точке D, причём AD = R.
реклама

Задачи. 1. В треугольник АВС вписана окружность радиуса R, касающаяся стороны АС в точке D, причём AD = R. а) Докажите, что треугольник АВС прямоугольный. б) Вписанная окружность касается сторон АВ и ВС в точках E и F. Найдите площадь треугольника BEF, если известно, что R = 2 и CD = 10. 2. На гипотенузу АВ прямоугольного треугольника АВС опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE. а) Докажите, что точки А, В, К и Е лежат на одной окружности. б) Найдите радиус этой окружности, если АВ = 24, СН = 7. 3. Окружность, вписанная в треугольник АВС, касается его средней линии, параллельной стороне ВС. а) Докажите, что АС + АВ = 3ВС. б) Найдите меньшую из сторон АВ и АС треугольника АВС, если известно, что его площадь равна 28,5 и ВС = 9,5. 4. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С1 и В1 соответственно. а) Докажите, что треугольник АВС подобен треугольнику АВ1С1. б) Найдите радиус данной окружности, если А = 300, В1С1 = 5 и площадь треугольника АВ1С1 в три раза меньше площади четырёхугольника ВС В1С1 5. В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N; АВ = 6, ВС = 5, АС = 9. а) Докажите, что биссектриса угла С делит отрезок MN пополам. б) Пусть Р – точка пересечения биссектрис треугольника АВС. Найдите отношение АР:PN.