Основные темы и типовые задачи по алгебре
реклама

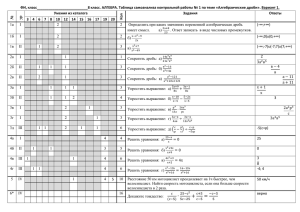
Математика Основные темы и типовые задачи по алгебре I. Рациональные дроби 1. При каких значениях р имеет смысл выражение: 2. Представить в виде дроби: a. ; b. ; c. 3. . Выполнить действия: a. ; b. ; c. 4. Привести дробь к знаменателю 5. Упростить: a 3 - 216 . 6. II. Зная, что a 2b a 2 , найти . b a Квадратные корни 1. Найти значение выражения: . a. ; b. ; c. 2. . Упростить: a. ; b. ; c. ; d. . 3. Вынести множитель из-под знака корня: 4. Внести множитель под знак корня: a. ; b. ; , если b<0. c. 5. Сравнить: 6. Освободиться от иррациональности в знаменателе: a. и c. 7. . ; b. III. , при b<0. ; . Построить график функции: Квадратные уравнения. Теорема Виета . 1. Решить уравнения: a. ; b. ; c. ; d. 2. . Решить методом замены переменной: a. ; b. ; c. 3. . Сократить дробь: . 4. 5. Составить квадратное уравнение с корнями: a. и b. и b. ; . Не вычисляя корней уравнения a. b. 7. . Составить квадратное уравнение с рациональными коэффициентами, если один из корней равен: a. 6. ; , найти: ; . При каком значении параметра a уравнение иметь равные корни будет IV. 1. 2. Построить график функции: a. f x 5x2 2 x 3 b. f c. f x x2 6 x 5 y = -2x + + 4; 2 x2 x 3 Найти значения коэффициэнтов a, b и c функции: y = ax 2 + bx + c , если график проходит через точки M (-1;0), A (-2;3), B (0;-9). 3. Найти значение коэффициэнта с и построить график функции : y = -x 2 + 4x +c , если известно, что наибольшее значение функции равно 2. V. Неравенства с одной переменной 1. Доказать неравенство: (6x - 5)(3x + 1) - (4x - 1)2 > x(x - 1) - 11. 2. Решить неравенства: 3. (4x - 3) 2 + (3x - 7)2 > (5x + 1)2 ; a. a. b. 2 < 12x - 51 < 8. При каких значениях x имеет смысл выражение: a. b. ;