Энергетические и скоростные свойства эллиптических орбит

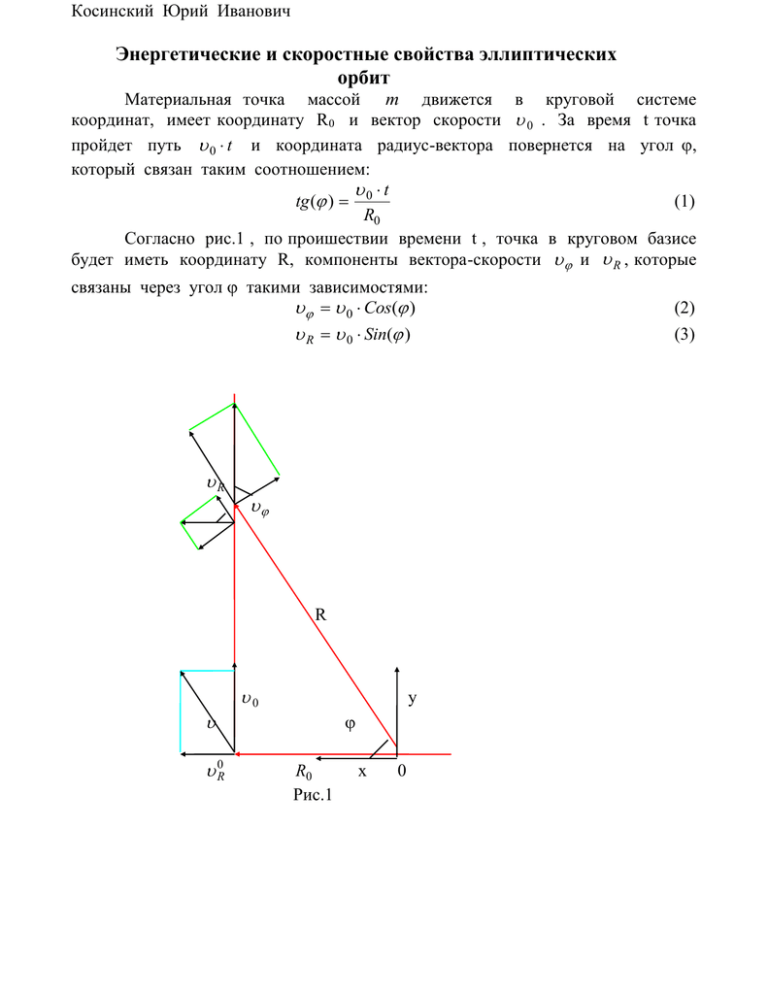
Косинский Юрий Иванович
Энергетические и скоростные свойства эллиптических
орбит
Материальная точка массой m движется в круговой системе
координат, имеет координату R0 и вектор скорости  0 . За время t точка
пройдет путь  0  t и координата радиус-вектора повернется на угол ,
который связан таким соотношением:
 t
(1)
tg ( )  0
R0
Согласно рис.1 , по проишествии времени t , точка в круговом базисе
будет иметь координату R, компоненты вектора-скорости   и  R , которые
связаны через угол  такими зависимостями:
   0  Cos( )
 R   0  Sin( )
R

R
0
y

 0R

R0
Рис.1
x
0
(2)
(3)
R0
(4)
Cos( )
Исключив из соотношений (2),(4) Сos(), получим очень важную зависимость,
которая будет применена в дальнейшем:
(5)
R    R0   0 ,
R
где слева равенства стоит произведение переменных величин, а справа
находится произведение констант-начальных условий.
В общем случае, когда начальный вектор имеет две составляющие  0
и  0R (см, рис.1), соотношения (2)-(3) запишутся в таком виде:
   0  Cos( )   0R  Sin( ) ;
   y  Cos( )   x  Sin( ) ,
 R   0  Sin( )   0R  Cos( ) ;
 R   y  Sin( )   x  Cos( ) .
Возьмем дифференциал от левой и правой части соотношения (1):
1

 d  0  dt .
2
R0
Cos ( )
(6)
(7)
(8)
Исключим функцию Cos2 ( ) с помощью соотношений (2), (4). В результате
получим:
R
(9)
d 
 dt .

В дальнейшем это соотношение будет использовано при замене переменных и
вычислении периода обращения тела на орбите..
Путем дифференцирования соотношений (2), (3) можно получить также
следующие зависимости:
d 
  R
d
d R
(10)
 
d
d 2 
 d  2
   0
Постановка задачи следующая: на тело (точку) массой m, имеющее
скорость  0 (максимальную), действует центральная гравитационная сила
a
(11)
F 2,
R
где a    m  M ,
(11A)
 - гравитационная постоянная,
m - масса тела,
M - центральная масса,
R - радиус-вектор расстояния между массами.
В декартовых координатах по осям x и y действуют соответствующие силы:
a
Fx   2  Cos( )
R
(12)
a
Fy   2  Sin( )
R
Соответствующие импульсы [1] силы обозначим так:
t
I x ( t )   Fx ( t ')  dt '
0
t
(13)
I y ( t )   Fy ( t ')  dt '
0
Подставив значения (9), (12) в соотношения (13) и учитывая равенство (5),
получим функциональные зависимости для импульсов:


a
a
I x ( )   
 Cos( ')  d '   
 Cos( ')  d '
R


R



0
0
0 0


a
a
I y ( )   
 Sin( ')  d '   
 Sin( ')  d '
R


R



0
0
0 0
(14)
Соответствующие им компоненты скоростей [1] имеют такую зависимость:
1
 I x (t )
m
1
 y ( t )   0y   I y ( t )
m
 x ( t )   0x 
Начальные условия следующие:
 0x  0
(15)
(16)
 0y   0
С учетом начальных условий и соотношений (14) компоненты скоростей примут
такой вид:

 x    B  Cos( ')  d '   B  Sin( ),
0
,

(17)
 y   0   B  Sin( ')  d '   0  B  B  Cos( ).
0
где введено обозначение : В - скоростной параметр орбиты.
1
a
(18)

m R0   0
Подставив функциональные зависимости (17) в соотношения (6). (7), найдем
зависимости для компонент скорости в круговом базисе:
    0  B  Cos( )  B
.
(19)
 R   0  B  Sin( )
Из функциональных зависимостей (19) следует, что при равенстве  0  B ,
радиальная составляющая скорости равна нулю, а угловая скорость имеет
постоянную величину, т.е. точка вращается по круговой орбите, Этот же вывод
следует из соотношений (17). При начальной скорости (угол )  0 больше
или меньше скоростного параметра орбиты В орбита принимает форму
эллипса. Из соотношения (17) для  y следует, что при  0 В
B
а при  0 В
 max   0 (  0)
,
 min  2B   0 (   )
 min   0 (  0)
 max  2B   0 (   )
.
(20)
(21)
где  max - максимальное значение скорости , которое может принимать тело
на орбите,  min - минимальное значение скорости, которое может принимать
тело на орбите.
Область возможных значений начальной скорости  0 (при сохранении
тела на замкнутой орбите ) находится в пределах: 0   0  2B .
(22)
Из соотношения (5) найдем функциональную зависимость от угла  для
радиуса орбиты.
R
R0   0

где e 
 R0 
0  B
0
B  ( 0  B )  Cos( )
 R0 
1
0  B
1 e
B
, (23)
 R0 
0  B
1

e

Cos
(

)
1
Cos( )
B
- эксцентриситет орбиты.
(24)
B
Как видно из формул (23), (24) , эксцентриситет орбиты e ,как параметр,
функционально заменяет скоростной параметр орбиты В
Согласно (22) эксцентриситет орбиты может находиться в пределах 1  e  1
и быть как положительным так и отрицательным числом .
(25)
При этом, если e  0 , R (   )  Rmax  R0 , а если e  0, R (   )  Rmin  R0 .
Эксцентриситет орбиты также можно выразить через (из (23))
экстремальные значения радиуса орбиты:
R  R0
e  max
 0,
Rmax  R0
(26)
Rmin  R0
e
 0.
Rmin  R0
А также
Rmax 1  e
, e>0.
(26A)

R0
1 e
Из
формул
(24), (20), (21) выразим
эксцентриситет
орбиты
через
экстремальные значения скорости тела на орбите:
   min
e 0
 0,
 0   min
(27)
 0   max
e
 0.
 0   max
А также
0
1 e
,
e>0.
(27A)

 min 1  e
На круговой орбите, когда начальная скорость равна скоростному
параметру орбиты :  0  B , из соотношения (18) следует
a
m   20 
,
(28)
R0
что удвоенная кинетическая энергия равна потенциальной энергии. Это и
есть физическое условие движения тела по круговой орбите. Равенство (28)
можно представить еще в таком виде:
m   20
(29)
 F (R0 ) .
R0
В формуле (29) представлено соотношение между силой, которая притягивает
к центру орбиты, радиусом кривизны орбиты , кинетической энергией
вращающегося тела, которое необходимо выполнять, чтобы тело двигалось по
круговой орбите.
Из соотношений (17) найдем абсолютную скорость вращающегося тела в
общем случае на эллиптической орбите.
(30)
 2   2x   2y  B 2  2  B  ( 0  B)  Cos( )  ( 0  B)2
На эллиптической орбите соотношение между начальной скоростью  0 и
скоростным параметром В согласно (24) можно представить в таком виде:
 0  B  (1  e)
(31)
В случае эллиптической орбиты равенство:  0  B и условие (равенство)
(28), (29) нарушается.
m   20
(29A)
 F ( R0 )  (1  e)
R0
Удвоенная кинетическая энергия может быть уже больше или меньше
потенциальной энергии. В связи с этим, в процессе движения тела на орбите,
происходит перекачка определенной части энергии из кинетической энергии в
потенциальную и наоборот. Покажем это на примере. Пусть  0  B , в
начальном состоянии (  0) удвоенная кинетическая энергия согласно (30)
равна
m   2 (  0)  m   20 .
(32)
Потенциальная енергия согласно (18) равна
a
m   20
(33)
 m  B 0 
 m   20
R0
1 e
и меньше удвоенной кинетической на величину:
 B
a
(33A)
m   20  m   0  B  m  0
0  B  e 
B
R0
Найдем различие кинетической энергии в двух экстремальных точках:
(=0) и (=) при этом будут использованы соотношения (18),(20),(24),(30),(31).
m   20 (  0) m   2min (   ) m 2

   0   20  4  B 0  B  2  m  B 0  B 
2
2
2
(34)




B
B


B
e
2

e
a
2  m  B2  0
 2  m B 0    0
 B 0 

  2  m
B
B 
1 e
1  e R0
0
Как видно из соотношения (34) после поворота на угол  кинетическая
2 e a
энергия тела уменьшилась на величину
 . При этом потенциальная
1  e R0
энергия увеличилась на эту же величину:

Rmax (   )

R0 (  0 )

R
 1
a max
1 
a 2 e

dR



a





.
R R0
 R0 Rmax  R0 1  e
R2
a
(35)
Здесь были использованы соотношения (23),(26). На круговой орбите
эксцентриситет орбиты e =0, начальное условие для скорости  0  B равно
скоростному параметру орбиты. Круговая орбита - это условный ноль отсчета.
На ней эксцентриситет орбиты равен нулю, начальные условия для скорости
и радиуса орбиты остаются неизменными при вращении тела по орбите. При
 0  B эксцентриситет орбиты становится e  0 , при движении тела по орбите
радиус и скорость изменяются, достигая при  своего Rmax ,  min . значения
которых выражаются соответствующими формулами. При  0  B можно
использовать
те
же
формулы,
заменив
в
них
e  ( e), Rmax  Rmin ,  min   max . Например, формулы
(34), (35) примут
такой вид:
m   20 m   2max (   )
2 e a


 ,
(36)
2
2
1  e R0
Rmin (  )

R0 (  0)
a
 dR  
2
R0
2 e a
 ,
1  e R0
(37)
где тело на орбите в экстремальной точке () имеет максимальную
скорость и минимальный радиус.
Из соотношений (34), (35) можно получить равенство :
m   20 m   2min
a
a
2 e a
(38)





2
2
R0 Rmax 1  e R0
откуда следует
m   20
a
m   2min a
(39)


 ,
2
Rmax
2
R0
что сумма кинетической и потенциальной ( в экстремально противоположных
точках орбиты) энергий сохраняется (Рис. 2). Из (38) также следует, что разница
между кинетической и потенциальной энергией тела в экстремальных точках
сохраняется:
m   20 a
m   2min
a
(40)



2
R0
2
Rmax
Такие зависимости вероятно связаны с тем, что вектор скорости кинетической
энергии и сила потенциальной энергии в экстремальных точках перпендикулярны
друг к другу. Результат (38), (39) можно обобщить на произвольное состояние
тела на орбите:
m   2 ( )
a
m   2 (   )
a
(41)



2
R (   )
2
R ( )
m   2 ( )
a
m   2 (   )
a
m   20 a
(42)





2
R ( )
2
R (   )
2
R0
Найдем размеры полуосей орбиты а0 и b0 , выраженные через начальные
условия  0 , R0 и эксцентриситет орбиты e . Большая полуось а0 равна
полусумме максимальному и минимальному радиусу R в
экстремальных
точках, т.е. согласно (23) получим:
1
1  e
1
a0   R0  R0 
(43)
  R0 
2
1  e
1 e
Малая полуось b0 пересекает орбиту в точке, где скорость орбиты  y  0
 y  0   0  B  B  Cos( ) ,
откуда следует угол этой точки  b :
 B  0 
 b  arccos
  arccos( e)
(44)
(45)
 B 
Подставив (45) в (23), найдем длину радиуса этой точки:
1 e
1
,
(46)
Rb  R0 
 R0 
2
1 e
1 e
Зная соотношение для радиуса (46), найдем величину малой полуоси из формулы:
1 e
 1

(47)
b0  Rb  Sin( b )  R0  
 1  e2   R0 
 1 e

1 e
По математическому определению [1] эксцентриситет есть величина
равная:
em 
c0
,
a0
(48)
где величина с0 равна:
c0  a02  b02
Подставив соотношения (43), (47) в (49), найдем параметр с0
e
1
1 e
c0  R0 


R

.
0
2
1

e
1

e
1

e
 
(49)
(50)
Выразим эксцентриситет из математического
определения (48) через
эксцентриситет из физического определения (24), (26), (27). Для этого
подставим соотношения (43), (50) в (48) и получим:
(51)
em  e
Если учесть, что физический эксцентриситет может быть как положительным,
так и отрицательным числом, эксцентриситеты совпадают.
Период времени обращения тела на орбите вычислим по формуле (9):
2
R ( )  d 2 R0   0
R0   0 2
d
T 
 

d





2
2
2


B


B




0
0
0
 Cos( )
1 0


B
(52)

R0
0
  1  e 
2
2

0
d
 1  e  Cos( ) 2
Здесь в преобразованиях были использованы соотношения (5), (19), (24), (31).
Согласно [2] интеграл в соотношении (52) решается следующим
образом.
2

0
d
 1  e  Cos( ) 2


1
1  e2
e  Sin( )
e  1  1  e  Cos( 
2

2

2

0
1
e2  1

2

0
0
d

1  Cos( )
d
2 
d



2 
1  Cos( ) 1  e 0 1  Cos( )








 (1  e)  tg 2   
2  2
  2 



arctg


1  e2  1  e2
1  e2

 
1  e2




0


3
(53)
2
Подставив соотношение (53) в (52), найдем функциональную зависимость для
периода времени обращения материальной точки на орбите от начальных условий
и параметров орбиты.
R0 (1  e) 2
R
1 e
(54)
T  2   
 2 0
3
0
0 1  e 3
2 2
1 e




Функционально период Т можно выразить и через другие параметры.
1
1  e  R0 0  1
a0  R0
 R0

.

1 e
1  e2  B  1  e2
В преобразованиях было использовано соотношение (24).
(55)
 R0 0  1


 B  B2
 2

2 3
1 e
2
R   1
T  2  0 0 
 B B
1
3
2 2
e
1  
m
 R0 0 


 B  mB  0 R0


(56)
3
T  2
1  e 
2 3
 2 a03
m
a
Здесь в преобразованиях были применены соотношения (55), (18). Использовав
соотношение (11А) , можно получить зависимость периода Т от гравитационной
постоянной и массы центральных сил.
a03
(57)
M
Если силу F в экстремальной точке R0 обозначить как произведение
массы на ускорение:
a
F   2   mg0 ,
(58)
R0
и применить это соотношение в функциональной зависимости (18):
a
g R
(59)
B
 0 0,
mR0 0
0
мы получим известное соотношение для первой и второй космической
скоромти в одной формуле.
B 0  g0 R0 ;  20  (1  e)g0 R0
(60)
 0  (1  e)g0 R0
T  2
Подставим соотношение (60) в функциональную зависимость (54):
R0 (1  e) 2
R0
 32
T= 2

2

1

e


3
0
g0
2 2
1 e

(61)

Здесь мы получили функциональную зависимость для периода эллиптической
орбиты в форме функции периода математического маятника. В левой части
соотношения (61) эксцентриситет можно менять за счет изменения ускорения g
в начальной экстремальной точке при неизменных начальных условиях R0 ,  0. В
правой части эксцентриситет можно менять за счет изменения скорости  в
начальной экстремальной точке при неизменных начальных условиях R 0, g0. Т.е.
за счет преобразований в соотношении (61) были изменены начальные условия
 0  g0 .
Следует заметить, что формула вычисления периода обращения тела на
орбите (52) выводится (9). Другой вариант формулы вычисления периода
обращения тела на орбите следует из физических соображений.
по
2
2
R ( )  d 2 R0   0  d R0
d
2
.
T 
 

 1  e  
1

(

)



(

)

2
2

0
0
0
0  1  e  Cos( ) 1  2Cos( )  e


(62)
Этот интеграл (62) функционально не вычисляется. Его можно вычислить только
на вычислительной машине. Для этого была составлена программа ellips на языке
FORTRAN и произведено численное вычисление (результат Т=). Параллельно
численно вычислялся интеграл (52) (результат Т1=), а также
функция
2 1.2245
(результат Т2=), численное значение которой близко с точностью до
(1  e )
одного процента (в пределах изменения эксцентриситета е 19.5)к результату
вычисления интеграла (62) (результат Т=) . Распечатка вычисления интегралов
(62),(52), и функции, заменяющей интеграл (62) приводится ниже.
Программа ellips
Введите данные: r0,v0,e,n
r0= .1000E+01 v0= .1000E+01 e= .0000E+00 n= 200
T= .6283E+01 T1= .6283E+01 T2= .6283E+01
Программа ellips
Введите данные: r0,v0,e,n
r0= .1000E+01 v0= .1000E+01 e= .3000E+00 n= 200
Т= .1195E+02 Т1= .1223E+02 Т2= .1192E+02
Программа ellips
Введите данные: r0,v0,e,n
r0= .1000E+01 v0= .1000E+01 e= .6000E+00 n= 200
Т= .2801E+02 Т1= .3142E+02 Т2= .2778E+02
Программа ellips
Введите данные: r0,v0,e,n
r0= .1000E+01 v0= .1000E+01 e= .9000E+00 n= 200
Т= .1733E+03 Т1= .2739E+03 Т2= .1733E+03
Программа ellips
Введите данные: r0,v0,e,n
r0= .1000E+01 v0= .1000E+01 e= .9500E+00 n= 200
Т= .4040E+03 Т1= .7848E+03 Т2= .4132E+03
Проанализировав результат вычисления, можно прийти к выводу, что если
следовать физическим соображениям, в функциональных зависимостях (54), (56),
(61) функцию (1  e2 )
(1  e2 ) 1.2245  (1  e2 )
примут вид
 32
 32
необходимо заменить на функцию
 (1  e2 )  .2755 . После этого формулы (54), (56), (61)
T  2
T  2
a03
R0
0



m
 1  e2
a
1 e
1 e


3
 .2755

1  e2

 .2755
,

a03
 2
 1  e2
M

(63)

 .2755
(64)

 .2755
3
R0
(65)
 1  e  2  1  e2
g0
В работе был представлен вывод функциональных зависимостей для орбит
вращения материальной точки массой m в поле центральных гравитационных сил
a
FR   2 . Представляет также интерес рассмотрения такого взаимодействия в
R
поле центральных сил обратно пропорциональных первой степени расстояния от
T  2
центра силы FR  

. По аналогии с соотношениями (14), (15) , компоненты
R
скоростей для такой центральной силы примут следующую функциональную
зависимость.
x 
 0x

1 Cos( )
 
d ,
m 0 

1 Sin( )
 y   0y  
d .
m 0 
(66)
Если принять к сведению, что компоненты скорости в декартовом и
круговом базисе связаны такой функциональной зависимостью
(67)
   x  Sin( )   y  Cos( ) ,
 R   x  Cos( )   y  Sin( ) ,
то можно прийти к выводу, что интегралы в соотношениях (66) в общем
аналитическом виде не решаются. Интегралы можно решить в частном случае,
когда выполняется условие
(68)
   0í  Cons tan ta,  R  0,  0x  0 .
В результате решения интегралов, компоненты скорости (66) примут следующую
функциональную зависимость.
 Sin( )
x   
m 
.
(69)
 Cos( )  1
 y    
m

Подставив значения функций для компонент скорости (69) в функциональные
зависимости (67), получим
 Sin2 ( )
 Cos2 ( )  Cos( )
  
    Cos( )  
m

m

,
(70)

 2 
m
 Sin( )  Cos( )
  Cos( )  1  Sin( )
R   
    Sin( )  
m

m

.
(71)
R  0
Проанализировав результат решения , можно прийти к выводу, что при силе
взаимодействия масс обратно пропорциональной первой степени радиуса
единственной замкнутой орбитой является круговая орбита со скоростью на
орбите не зависящей от радиуса орбиты и массы тела на орбите.

(72)
 
 M
m
Удвоенная кинетическая энергия тела на орбите равна
m  2  
потенциальной энергии (для центральной силы -
(73)

). Соотношение (73)
R
аналогично соотношению (28). Соотношение на орбите между кинетической
энергией, силой и радиусом кривизны такое же как и в соотношении (29)
m   2

 F (R )  .
(74)
R
R
Если силу F на круговой орбите обозначить как произведение массы на
ускорение
F

(75)
 m  g ,
R
то из соотношений (74), (75) следует
(76)
  Rg
соотношение аналогичное (60). В данном случае в подкоренном выражении
произведение есть величиной постоянной.
Период обращения тела на круговой орбите
R
R
(77)
T  2
 2

g
также функционально совпадает с известным соотношением (61).
Чтобы доказать, что совпадение формул (74) и (29), (76) и (60), (77) и (61)
для различных сил взаимодействия не случайно, рассмотрим взаимодействие масс
m и M с силой F, не зависящей от расстояния между ними (постоянной
величиной)
F   .
(78)
Интегральные уравнения для компонент скорости тела на орбите (учитывая
последовательность вывода для предыдущих типов взаимодействия) имеют
следующую функциональную зависимость
  R 
 x      Cos ( )  d
m 0   
(79)


R
 y   0y     Sin( )  d
m 0   
Решить эту систему интегральных уравнений можно при условии нахождения
тела на стационарной орбите, когда
 R
   Cons tan ta
  
(80)
Результат решения
x  
 R
  Sin( )
m    
 y   0y 
(81)
 R
   Cos( )  1
m    
Подставив полученные функциональные зависимости (81) в соотношения (67)
получим систему уравнений
 Sin2 ( )
 Cos2 ( )  Cos( )
0
  
  y  Cos( )  
m   
m
  
 
 
 R
 R
 Sin( )  Cos( )
  Cos( )  1 Sin( )
R   
  0y  Sin( )  
m
m
  
  
 
 R
  
где неизвестными являются   ,  R ..
 R
Результат решения для круговой орбиты
   
 0y     ,  R  0,
 R m
(82)
 
 R
(83)
   
      ,     0y .
 R m
Из соотношения (83) сразу следует
m   2
F
(84)
R
соотношение между кинетической энергией, крутизной орбиты и центральной
силой, которое выполняется для тела на круговой орбите радиусом R (аналогия
(29), (74) для других сил взаимодействия). Умножив левую и правую часть
соотношения (84) на радиус R, получим известный результат для других сил
взаимодействия (28),(73), что удвоенная кинетическая энергия равна
потенциальной
m   2  F  R
(85)
Обозначив силу F как произведение массы m на ускорение g из формулы
(84) получим соотношение для скорости тела, находящегося на круговой орбите
(86)
  R  g
по форме совпадающее для других сил взаимодействия (60), (76).
Подставив значение скорости (86) в формулу для периода обращения тела
на круговой орбите, получим известное соотношение для других сил
взаимодействия (61), (77)
R
R
(87)
T  2
 2

g
В итоге можно сказать следующее: было рассмотрено движение
материальной точки массой m по круговой орбите в поле центральных сил трех
a

типов F2   2 , F1   , F0    . Было найдено соотношение между
R
R
кинетической энергией, силой взаимодействия на орбите и радиусом орбиты,
которое необходимо выполнять, чтобы тело находилось на стационарной
круговой орбите. Формула этого соотношения для трех типов центральных сил
одна и та же и не зависит от типа взаимодействия, включая промежуточные
значения.
m   2
F
(88)
R
Из этого главного соотношения следует, как следствие, формула для скорости
тела на орбите
(89)
  R  g ,
а также формула для периода обращения тела на орбите
R
,
(90)
T  2 
g
которые справедливы для всех рассмотренных типов центральных сил
взаимодейсивия.
Если равенство (88) на орбите не выполняется, круговые орбиты
превращаются в эллиптические. Для центральной силы F2 эллиптические орбиты
замкнуты (орбиты замыкаются сами на себя). Для центральных сил F1, F0 в случае
неравенства (88) задача не решается. Это связано с тем, что орбиты принимают
какуюто произвольную форму и не замыкаются сами на себя (орбиты
незамкнуты).
Для центральной силы F2 задача имеет решение даже в случае неравенства
(88). Для этой силы взаимодействия была полностью решена задача, найдены
координатные, скоростные, энергетические, временные характеристики
нахождения тела на орбите в зависимости от начальных параметров и
характеристических параметров орбиты.
y
0
x
*
R0
*
Rmax
*
 min
Рис. 2
y
0
x
*
R0
* Rmin *
 max
Рис. 3
y
 ( )
x
*
R
*
 (   )
*
R
Рис. 4
Литература
1. Ю.И. Косинский, Энергия материальной точки, 1, (2001).
2. И.Н. Бронштейн, К.А. Семендяев, Справочник по математике, 371,
(1962).