Одномерная выборка
реклама
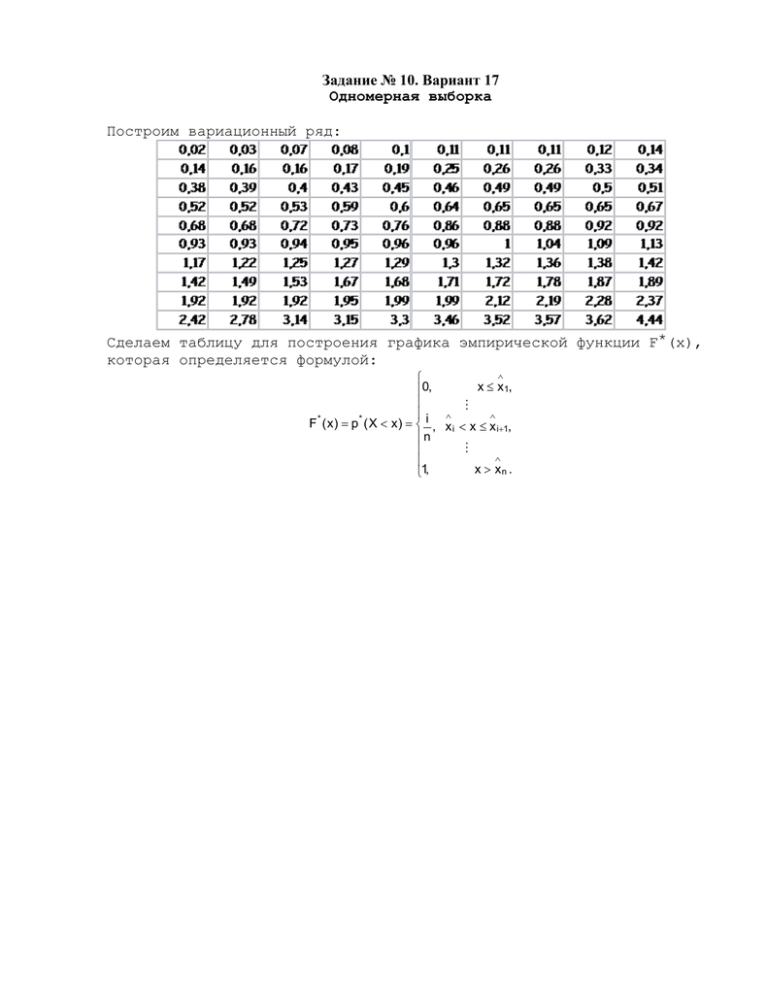
Задание № 10. Вариант 17 Одномерная выборка Построим вариационный ряд: Сделаем таблицу для построения графика эмпирической функции F*(x), которая определяется формулой: x x1, 0, i * * F ( x ) p ( X x ) , x i x x i1, n x xn . 1, k - количество одинаковых чисел в выборке, m - номер числа в вариационном ряду График эмпирической функции представлен в конце задания вместе с графиком гипотетической функции F0(x). Определим количество непересекающихся и примыкающих друг к другу M интервалов: M M 10 int n Где n 100 - количество чисел в выборке Построим гистограмму равноинтервальным методом: Aj j M j h 1 x1 x1 h ... ... ... ... ... x1 M h h M x 1 (M 1) h Определим длину интервала: Xn X1 hj 1 M h Bj h 0.442 p *j f j* 1 n p1* h ... ... M * pM h n f*(x) 0.6 0.5 0.4 0.3 0.2 0.1 0 1 2 3 4 5 x Построим гистограмму равновероятностным методом: j Aj Bj x11 x10 2 hj j p *j f j* B1 A 1 n M 1 M p1* h1 1 x1 2 x11 x10 2 x 21 x 20 2 B2 A 2 n M 1 M p *2 h2 ... ... ... ... ... ... ... M x M (M1)1 x M (M 1) 2 BM A M n M 1 M * pM hM xn f*(x) 1 0.8 0.6 0.4 0.2 0 1 2 3 4 5 x Вычислим точечные оценки числовых характеристик: Состоятельная оценка математического ожидания: mx x 1 n n mx 1.154 xi i 1 Несмещенная состоятельная оценка дисперсии: 2 S0 n 1 n1 2 xi i 1 n n1 2 x 2 S0 0.928 Несмещенная состоятельная оценка среднеквадратического отклонения: S0 2 S0 0.963 S0 Вычислим интервальные оценки математического ожидания и дисперсии с надежностью =0.95. Доверительный интервал для математического ожидания: Согласно центральной предельной теореме при достаточно большом n закон распределения можно считать нормальным, поэтому воспользуемся следующей формулой для случайной величины X с неизвестным законом распределения: S0 z S0 z x mx x n n где z=arg(/2)=arg(0.475)=1.96 - значение аргумента функции Лапласа, тогда интервал равен: 0,965 < mx < 1,343 Доверительный интервал для дисперсии: 2 S0 z 2 2 2 S Dx S0 z n1 0 2 n1 2 S0 0,669 < Dx < 1,186 Выдвинем двухальтернативную гипотезу о законе распределения случайной величины: Но - величина Х распределена по экспоненциальному закону e t , t 0 f (t ) f0 (t ) ; F( t ) F0 ( t ) t0 0, 1 e t , t 0 t0 0, Н1 - величина Х не распределена по экспоненциальному закону f ( x ) f 0 ( x ) ; F( x ) F0 ( x ) Определим оценки неизвестных параметров гипотетического закона распределения: 1 x 0.866 Проверим гипотезу с помощью критерия 2. Вычислим значения критерия 2 на основе равноинтервального статистического ряда. Теоретические вероятности попадания случайной величины вычислим по формуле: Bi Ai x x pi Fo Bi Fo Ai 1 e 1 e Данные для расчета теоретических вероятностей представлены в таблице: Определим значение критерия 2 по формуле: 2 M n i 1 pi p''i2 pi Найдем значения критерия для каждого значения, а затем общий. Тогда, значение критерия равно: 2 12.027 Определяем число степеней свободы: k=M-1-s, где s - число параметров, от которых зависит выбранный гипотезой H0 закон распределения, s1 k8 При заданном уровне значимости =0.05 сравним полученное значение критерия 2 со значением 2,k из таблицы распределения 2, которое равно: 2k 15.51 Поскольку 2<2,k, то гипотеза H0 принимается. Проверим гипотезу с помощью критерия Колмогорова: Выберем 20 значений из вариационного ряда для данного критерия и вычислим значения гипотетической функции: По графику определим максимальное отклонение между функциями F*(x) и F0(x): Z 0.0729 Определяем значение критерия: nZ 0.729 Из таблицы распределения Колмогорова выбираем критическое значение , где =1-=0.95 =1.36 Поскольку , то гипотеза H0 принимается. Построим график гипотетической функции F0(x) совместно с графиком эмпирической функции распределения F*(x): F*(x), Fo(x) 1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0.45 0.9 1.35 1.8 2.25 X 2.7 3.15 3.6 4.05 4.5 Задание № 11. Вариант 17 Двумерная выборка - количество двумерных чисел Вычислим точечную оценку коэффициента корреляции: n 50 Оценки математических ожиданий: mX mY x 1 n y 1 n n xi mX 4.546 yi mY 5.483 i 1 n i 1 Оценки дисперсий: So ( x ) n1 1 2 D( y) n 1 2 D( x) So ( y ) n1 xi yi i 1 n n 2 n1 n 2 i 1 n1 2 x D( x) 10.783 D ( y) 9.827 2 y Состоятельная оценка корреляционного момента равна: n 1 KXY n1 xi yi i 1 n n1 x y KXY 10.091 Состоятельная оценка коэффициента корреляции равна: KXY RXY 2 RXY 0.98 2 So ( x ) So ( y ) Вычислим интервальную оценку коэффициента корреляции с надежностью =0.95 по формуле: 2a e 2a e 1 1 2b RXY e 1 2b e 1 1 RXY z z 1 RXY b 0.5 ln n3 n3 1 RXY 1 RXY z - значение аргумента функции Лапласа, т.е. Ф(z)=/2=0.95/2=0.475, которое в нашем случае равно 1.96. Тогда коэффициенты a и b равны: Где a 0.5 ln a 2.02 b 2.592 Таким образом, доверительный интервал для коэффициента корреляции имеет вид: I(Rxy)=[0,965 ; 0,989] Проверим гипотезу об отсутствии корреляционной зависимости: H0 : R XY 0 ; H1 : R XY 0 Определяем значение критерия: Z RXY n Z 35.114 2 1 RXY Из таблицы функции Лапласа определяем критическое значение Z, которое равно 1.96. Гипотеза Ho отклоняется, поскольку Z>Za Вычисляем оценки параметров а0 и а1 линии регрессии y( x) a1 a0 a1 x KXY Sо ( x ) a1 0.936 2 a0 mY a1 mX a0 1.229 Построим диаграмму рассеивания и линию регрессии: y 12 10 8 6 4 2 2 0 2 4 6 2 x 8 10









