Электротехника (ТОЭ) РГР № 3
реклама
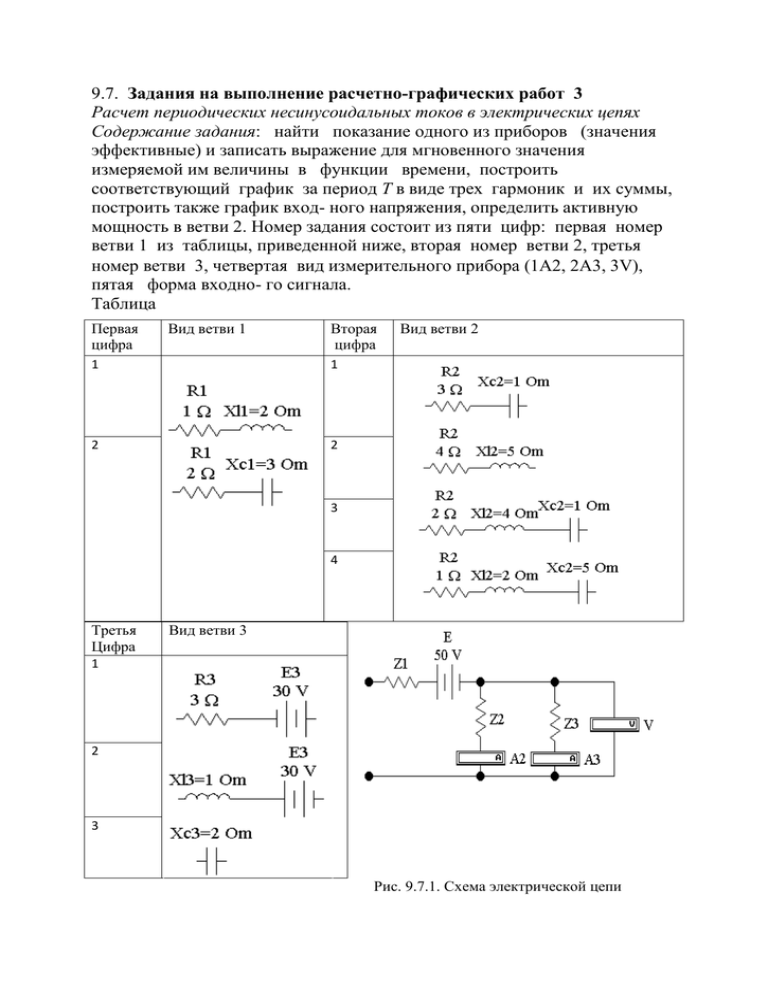
9.7. Задания на выполнение расчетно-графических работ 3 Расчет периодических несинусоидальных токов в электрических цепях Содержание задания: найти показание одного из приборов (значения эффективные) и записать выражение для мгновенного значения измеряемой им величины в функции времени, построить соответствующий график за период Т в виде трех гармоник и их суммы, построить также график вход- ного напряжения, определить активную мощность в ветви 2. Номер задания состоит из пяти цифр: первая номер ветви 1 из таблицы, приведенной ниже, вторая номер ветви 2, третья номер ветви 3, четвертая вид измерительного прибора (1А2, 2А3, 3V), пятая форма входно- го сигнала. Таблица Первая цифра Вид ветви 1 Вторая цифра 1 1 2 2 Вид ветви 2 3 4 Третья Цифра Вид ветви 3 1 2 3 Рис. 9.7.1. Схема электрической цепи Форма входного напряжения u(t) и его представление гармоническим рядом 1. Прямоугольные импульсы c амплитудой Um = 150 В: 1 T 0.02 с, t 0 0.00005 T , 2 T , . f31 ( t) 150 if 0 t 0.5 T ( 150) if 0.5 T t T 200 100 f31 ( t ) 0 100 200 510 0 3 0.01 0.015 0.02 t Рис. 9.7.2. Прямоугольные импульсы 4 Um 1 1 u1 ( t) sin ( t) sin ( 3 t) sin ( 5 t) ... , Um 150. 3 5 Представление входного сигнала суммой трех гармоник: 4 Um 4 Um f2 ( t) sin ( t), f3 ( t) sin ( 3 t), 3 4 Um f4 ( t) sin ( 5 t), f5 ( t) f2 ( t) f3 ( t) f4 ( t). 5 200 150 f2 ( t ) 100 f3 ( t ) 50 f4 ( t ) 0 f5 ( t ) 50 100 150 200 0 2.510 3 510 3 7.510 3 0.01 0.0125 0.015 t Рис. 9.7.3. Спектр прямоугольного импульса 0.0175 0.02 2. Трапецевидные симметричные импульсы с амплитудой Um = 150 B и временем нарастания ta = 3T/16. Входной сигнал представим суммой линейных функций, имеющих скорость нарастания k = Um/ta и включаемых в нужные моменты времени при помощи функции Хевисайда Ф(t): T 150 3 , k , k 4 104 , ta 3 , ta 3.75 10 16 ta f6 ( t) k t ( t) k ( t ta) ( t ta), f7 ( t) k [ t ( 0.5T ta) ] [ t ( 0.5T ta) ], f8 ( t) k [ t ( 0.5T ta) ] [ t ( 0.5T ta) ], f9 ( t) k [ t ( T ta) ] [ t ( T ta) ], f10 ( t) f6 ( t) f7 ( t) f8 ( t) f9 ( t), 3 . 8 200 100 f10 ( t ) 0 100 200 3 510 0 u2 ( t) 4 Um 0.01 0.015 0.02 t Рис. 9.7.4. Трапецевидный импульс sin ( ) sin ( t) 1 sin ( 3 ) sin ( 3 t) . 9 1 sin ( 5 ) sin ( 5 t) ... 25 Представление входного сигнала суммой трех гармоник: 4 Um 4 Um sin ( 3 ) sin ( 3 t) , f11 ( t) sin ( ) sin ( t), f12 ( t) 9 4 Um sin ( 5 ) sin ( 5 t) , f14 ( t) f11 ( t) f12 ( t) f13 ( t). f13 ( t) 25 200 150 100 f11 ( t ) f12 ( t ) f13 ( t ) 50 0 f14 ( t ) 50 100 150 200 0 2.510 3 510 3 7.510 3 0.01 0.0125 0.015 0.0175 0.02 t Рис. 9.7.5. Спектр трапецевидного импульса 3. Треугольные симметричные импульсы с амплитудой Um = 150 B. Построим входную функцию путем задания ее значений в нескольких точках, применив линейную аппроксимацию для нахождения промежуточных значений: Yi ( 0 150 0 150 0 ) строка-вектор исходных значений функции, T Y Yi - столбец, N length ( Y ) - число элементов строки, T - шаг по t, i 0 N 1 - число шагов, T 0.02 - период, dt N 1 tsi i dt - текущее время, Y ( t) linterp ( ts Y t) - линейная интерполяция. 100 Y (t) 0 100 0 3 510 0.01 0.015 t Рис. 9.7.6. Треугольный импульс 0.02 u3 ( t) 8 Um 2 sin ( t) 1 1 sin ( 3 t) sin ( 5 t) .... . 9 25 Представление входного сигнала суммой трех гармоник: f15 ( t) 8 Um f17 ( t) 2 8 Um 25 2 sin ( t), f16 ( t) 8 Um 9 2 sin ( 3 t), sin ( 5 t), f18 ( t) f15 ( t) f16 ( t) f17 ( t) . 150 f15 ( t ) f16 ( t ) f17 ( t ) 100 50 0 f18 ( t ) 50 100 150 0 510 3 0.01 0.015 0.02 t Рис. 9.7.7. Спектр треугольного импульса 4. Косинусоида (по модулю) амплитудой Um = 100 B 100 75 f19 ( t ) 50 25 0 0 510 3 0.01 0.015 t Рис.9.7.8. Косинусоида (по модулю) 0.02 u4 ( t) 4 Um 1 1 1 1 cos ( 2 t) cos ( 4 t) cos ( 6 t) ... 15 35 2 3 Представление входного сигнала суммой трех гармоник и постоянной составляющей: 4 Um 4 Um cos ( 2 t) 4 Um cos ( 4 t) , f21 ( t) , f22 ( t) , f20 ( t) 2 3 15 4 Um cos ( 6 t) , f24 ( t) f20 ( t) f21 ( t) f22 ( t) f23 ( t). f23 ( t) 35 100 f21 ( t ) 50 f22 ( t ) 0 f23 ( t ) f24 ( t ) 50 100 0 510 3 0.01 0.015 0.02 t Рис. 9.7.9. Спектр косинусоиды (по модулю) 5. Пилообразные импульсы амплитудой Um=100 B : f25 ( t) ( 5000 t) if 0 t T f25 ( t T ) if t T 100 f25 ( t ) 50 0 0 510 3 0.01 0.015 t Рис. 9.7.10. Пилообразный импульс 1 1 1 1 u5 ( t) Um sin ( t) sin ( 2 t) sin ( 3 t) ... 2 3 2 0.02 Представление входного сигнала суммой трех гармоник и постоянной составляющей: Um Um Um , f27 ( t) f26 ( t) sin ( t), f28 ( t) sin ( 2 t), 2 2 Um f29 ( t) sin ( 3 t), f30 ( t) f26 ( t) f27 ( t) f28 ( t) f29 ( t). 3 Рис. 9.7.11. Спектр пилообразного импульса 100 f27 ( t ) f28 ( t ) 50 f29 ( t ) f30 ( t ) 0 50 0 510 3 0.01 0.015 0.02 t Расчетно-графическая работа 3. Пример выполнения Рис. 9.7.12. Схема электрической цепи. (Приборы измеряют эффективные значения, а с индексом dc измеряют постоянные токи и напряжения.) Рис. 9.7.13. Схема на постоянном токе Рис. 9.7.14. Схема на переменном токе Входная функция f ( t) пилообразные импульсы с амплитудой Е = 100 В и периодом T = 0.02 с: 3 x T 0.02, x 0 0.001 2 , 2 , f ( x ) 5 10 , T n 1 5 . Вычисление коэффициентов Фурье прямым интегрированием: 2 1 a0 2 0 bn 2 1 f ( x ) dx, bn 0 f ( x ) sin ( n x ) dx, -31.831 -15.915 -10.61 2 1 an 0 -7.958 f ( x ) cos ( n x ) dx, an 0, a0 50 -6.366 Значения первых трех гармоник и их сумма: f1 ( t) 31.83 sin ( t), f2 ( t) 15.91 sin ( 2 t), f3 ( t) 10.61 sin ( 3 t), f4 ( t) f1 ( t) f2 ( t) f3 ( t), V0 50 Вычисление коэффициентов Фурье при помощи быстрого преобразования: T 3 , A FFT ( f ), h 0 511, f h 5 10 h 511 Vn V n A n if n 1 -31.893 A n 2 if n 0 -15.947 -10.632 -7.974 -6.38 40 f1 ( t ) 20 f2 ( t ) f3 ( t ) f4 ( t ) 0 20 40 0 510 3 0.01 0.015 0.02 t Рис.9.7.15. Спектр входного сигнала k 1 3, V1 20 В, V2 40 В, R1 1 Ом, R2 2 Ом, R3 3, Ом, Xl2 4 Ом, Xc1 5 Ом, Xl1 2 Ом, U k 100 ( k ) 1 . Вектор амплитуд гармоник согласно справочникам: Uk -31.831 -15.915 -10.61 Расчет сопротивлений: z1 k R1 j k Xl1, z2 k R2 j k Xl2, z3 k R3 j Xc1 , k 1 z23 k z2 k z3 k z2 k z3 k , z k z1 k z23 k. V0 V1 V2 Расчет токов: i0 , i1k U k z k 1, U23k i1k z23 k, R1 R2 i2k U23k z2 k , i3k U23k z3 k 1, u0 i0 R2 V2. 1 Показания приборов I1 3 2 i0 0.5 , V i1k , I2 2 3 2 i0 0.5 k1 3 I3 0.5 i3k i2k U23k 2. 2, k1 2 k1 2 u0 0.5 3 k1 Активная мощность в ветви с резистором R2 2 P I2 R2. Результат расчета: i0 3.333 А, u0 33.333 В, I1 5.155 А , I2 5.137 А, I3 3.725 А, V 38.407 В, P 52.777 Вт, 3 k arg i3k , f5 ( t) i31 sin t 3 1, f6 ( t) i32 sin 2 t 3 2, f7 ( t) i33 sin 3 t 3 3, f8 ( t) f5 ( t) f6 ( t) f7 ( t). 10 f5 ( t ) 5 f6 ( t ) f7 ( t ) 0 f8 ( t ) 5 10 0 510 3 0.01 0.015 0.02 t Рис. 9.7.16. Форма тока i3 по результатам расчета Рис. 9.7.17. Форма тока i3 и входного напряжения по результатам моделирования Здесь V3 V4 V5 это эффективные значения гармоник, соответствующие амплитудам U k и V n. Имеем из показаний приборов: I1 = 3.935 A, i0 = 3.378A, V = 19.12 B, Vdc = 33.05 B. Отсюда: 2 2 3.935 3.378 5.186 А, 2 2 19.12 33.05 38.182 В.





