Задания для зачета по алгебре 12 класс

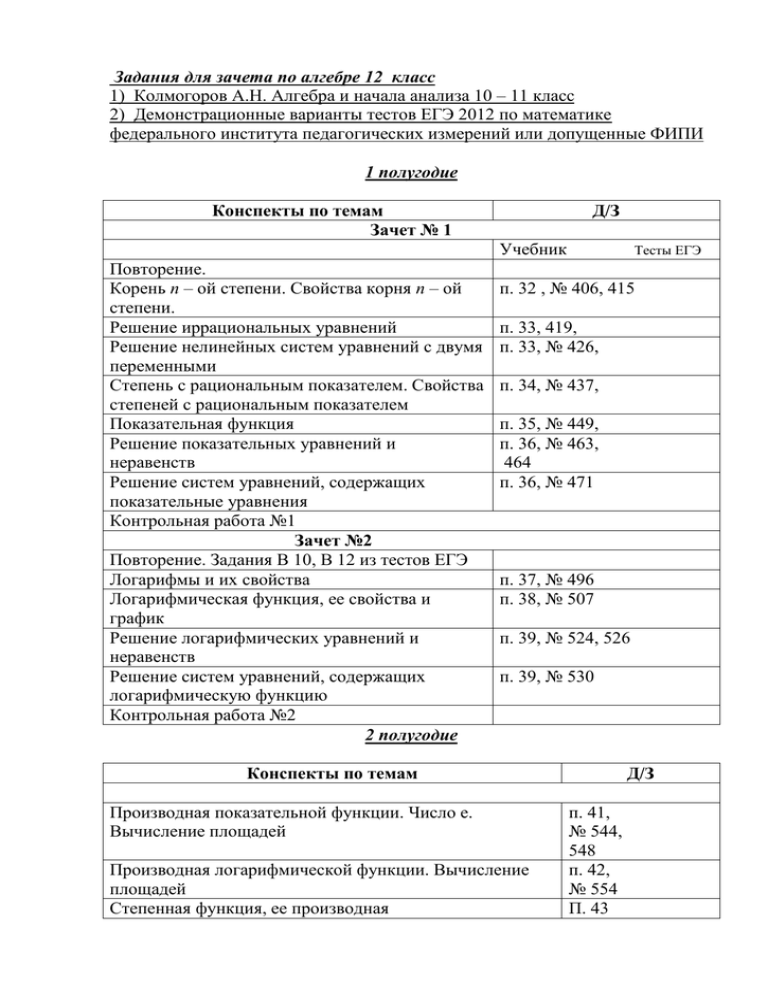
Задания для зачета по алгебре 12 класс
1) Колмогоров А.Н. Алгебра и начала анализа 10 – 11 класс
2) Демонстрационные варианты тестов ЕГЭ 2012 по математике
федерального института педагогических измерений или допущенные ФИПИ
1 полугодие
Конспекты по темам
Зачет № 1
Д/З
Учебник
Повторение.
Корень п – ой степени. Свойства корня п – ой
степени.
Решение иррациональных уравнений
Решение нелинейных систем уравнений с двумя
переменными
Степень с рациональным показателем. Свойства
степеней с рациональным показателем
Показательная функция
Решение показательных уравнений и
неравенств
Решение систем уравнений, содержащих
показательные уравнения
Контрольная работа №1
Зачет №2
Повторение. Задания В 10, В 12 из тестов ЕГЭ
Логарифмы и их свойства
Логарифмическая функция, ее свойства и
график
Решение логарифмических уравнений и
неравенств
Решение систем уравнений, содержащих
логарифмическую функцию
Контрольная работа №2
2 полугодие
Тесты ЕГЭ
п. 32 , № 406, 415
п. 33, 419,
п. 33, № 426,
п. 34, № 437,
п. 35, № 449,
п. 36, № 463,
464
п. 36, № 471
п. 37, № 496
п. 38, № 507
п. 39, № 524, 526
п. 39, № 530
Конспекты по темам
Производная показательной функции. Число е.
Вычисление площадей
Производная логарифмической функции. Вычисление
площадей
Степенная функция, ее производная
Д/З
п. 41,
№ 544,
548
п. 42,
№ 554
П. 43
Зачет №3
Тесты ЕГЭ 2011
Элементы комбинаторики
Повторение курса 10 – 12 классов
Контрольная работа № 3
Контрольная работа № 1
1. Найдите область определения, множество значений, промежутки
возрастания, убывания функции у = 2х
2. Решите уравнения и неравенства
1) 2х-3 = 4
2) зх  1  1
3) 3х+2 – 5*3х = 324
4) 9х – 7*3х – 18 = 0
5) 210х-5 >
1
16
6) 22х + 6х = 2*32х
3. Если наблюдатель находится на небольшой высоте h над поверхностью
Земли, то расстояние от него до линии горизонта можно найти по
формуле l= 2RH , где R=6400 км – радиус Земли. Найдите наименьшую
высоту, с которой должен смотреть наблюдатель, чтобы он видел линию
горизонта на расстоянии не менее восьми километров? (Ответ выразите в
метрах).
4. Найдите значение выражения 4+ 51/3 * 3√25
5. Решите систему уравнений
32х – 2siny=0
4cos2y + 4cosy -3 =0
Контрольная работа № 2
1. Найдите область определения, промежутки возрастания и убывания,
область значений функции f(x) = log2 x . Постройте ее график.
2. Найдите значение выражения 25log53
3. Решите уравнения и неравенства
1) log7(х-6)=2
1) log22 x – 4 log2x = 12
2) log0,1 (7x + 3) > - 1
3) log2 x4 – log0,25 x = log3 3√3
4) logx+3(9-x2) -
1
logx+3(х-3)2 ≥ 2
16
5) log 9( 2*18х – 4х) = 2х
4. Наблюдение за космическим телом показало, что расстояние S ( в
километрах) между этим телом и Землей увеличивается по закону
S = 1,8*105 + 0,5*105 * t , где t –время в секундах от момента начала
наблюдения. Через сколько секунд после начала наблюдения скорость
удаления тела от Земли составит 103 км/с.?
5. Найдите производные функций
1) y= ln (x-3)
2) y = lnx + π -1
3) y = ex + sinx
6. Найдите наименьшее значение функции у = (х-6)ех-5 на отрезке [4;6]
Контрольная работа №3
Задания из демонстрационных вариантов ЕГЭ федерального института
педагогических измерений или допущенных ФИПИ (на бумажной основе или
из Интернета)
Задания для зачета по геометрии 12 класс
1)Атанасян Л.С. Геометрия 10 – 11 класс
2) Демонстрационные варианты тестов ЕГЭ 2012 года по математике
федерального института педагогических измерений или допущенных ФИПИ
1 полугодие
Конспекты по темам
Зачет № 1
Д/З
Учебник
Повторение.
Понятие объема. Свойства объемов
Объем прямоугольного параллелепипеда
Объем призмы
Объем пирамиды
Тесты ЕГЭ
п. 63
п. 64, № 649,
652
п. 65, 68, № 659,
660
п. 69, № 684,
691
Контрольная работа № 1
2 полугодие
Конспекты по темам
Зачет № 2
Д/З
Объем цилиндра
Объем конуса
Объем шара и его частей
Площадь сферы
Итоговое повторение
Контрольная работа № 2
Учебник
Тесты ЕГЭ
п. 66, № 666,
667
п. 70, № 702,
705
п. 71 – 72, № 713,
717
п. 73, № 723
Тесты ЕГЭ 2011
Контрольная работа № 1
1. Объем прямоугольного параллелепипеда равен 64. Чему будет равен
объем параллелепипеда, если каждое его ребро уменьшить в 4 раза?
2. Объем данного правильного тетраэдра равен 2 см3. Найдите объем
правильного тетраэдра, ребро которого в 3 раза больше ребра данного
тетраэдра?
3. Вычислите объем правильной треугольной призмы, сторона основания
которой 6 см, высота призмы 14см.
4. В правильной четырехугольной пирамиде высота 12см, а боковое ребро
наклонено к плоскости основания под углом 450. Найти объем пирамиды.
5. Длины сторон основания прямого параллелепипеда 10см и 5 2 см,
величина угла между ними 450. Найти объем, если длина меньшей диагонали
10см.
6. У треугольной пирамиды SABC грань АВС – правильный треугольник.
Высота пирамиды, проведенная из вершины А, составляет с плоскостью
грани АВС угол, равный arcsin
2
. Найдите градусную меру угла между этой
3
высотой и ребром АВ.
Контрольная работа № 2
1. Конус и цилиндр имеют общее основание и общую высоту. Вычислите
объем цилиндра, если объем конуса равен 2.
2. Объем конуса равен 1,5. Радиус основания увеличили в 2 раза, а высоту
уменьшили в 3 раза. Найдите объем получившегося конуса.
3. Шар объемом 9см3 вписан в цилиндр. Найдите объем цилиндра. Ответ
дайте в см3.
4. В основании прямой призмы лежит прямоугольный треугольник с
катетами 7 и 8. Боковые ребра равны
8

. Найдите объем цилиндра,
описанного около этой призмы.
5. Точки М и N расположены на окружностях верхнего и нижнего оснований
цилиндра, высота которого 5 см. Площадь сечения цилиндра плоскостью,
проходящей через МN параллельно оси цилиндра, равна 48 см2. Расстояние
от оси цилиндра до плоскости сечения 3 см. Найдите объем цилиндра.
6. Задания из демонстрационных вариантов ФИПИ 2012г. или допущенных
ФИПИ за курс средней школы