Решение заданий олимпиады учителей по физике

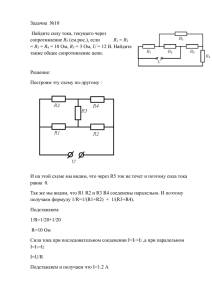
Решение заданий олимпиады учителей физики
2010 год
Задание 1.
Построим график зависимости модуля силы трения Fтр
от пути, пройденного санками S. Площадь под графиком
равна работе силы трения. Работа силы трения равна
уменьшению механической энергии санок
m V2/2 = kmg (S – L/2)
Отсюда получаем
S = V2/2kg = L/2
Подставляем данные задачи и получаем S = 2,8 м.
Задание 2.
При температуре Т1 запишем уравнение Клапейрона – Менделеева для газа в нижней и
верхней частях цилиндра
P1 V1 = R T1
P2 β1 V1 = R T1
Разность давлений снизу и сверху массивного поршня равна
P1 – P2 = m g/ S
,где m
- масса поршня, а S – его площадь
Обозначим через V сумму объёмов верхней и нижней частей, тогда
V = V1 (1 + β1 )
После преобразований получаем
mg / S = R T1 (1 – 1/β1)/V
Аналогично при температуре Т2
mg/S = R T2 ( 1 – 1/β2)/ V
(1)
(2)
Разделив ( 2 ) на ( 1 ), получаем
T2 = T1 ( β1– 1/β1 ) / ( β2 – 1/β2)
Подставив в ( 3 ) данные задачи, получаем Т2 = 420 К
(3)
Задание 3.
этап
Содержание этапов
Записана формула для дефекта массы в реакции
m   M нач  M кон 
1
2
3
Записан закон сохранения энергии
E  m  c 2
Введен энергетический эквивалент атомной единицы массы. Получен
численный ответ:
приблизительно 3 Мэв.
Задание 4.
ЭДС всей батареи ε0 = nε. Полное сопротивление цепи R0  nr  R . Сила тока в цепи

n
.
I 0 
R0 nr  R
и на сопротивлении R нагрузки выделяется мощность
P  I 2R .
Из соотношений (1) и (2) получим
(1)
(2)
nrI 2  nI  P  0 .
Решив последнее уравнение относительно I, найдем силу тока в цепи:
I1 
или
n  n 2 2  4nrP
 2,67A
2nr
n  n 2 2  4nrP
I2 
 2A .
2nr
Для ответа на второй вопрос необходимо найти зависимость мощности P,
выделяющейся во внешней цепи, от сопротивления R нагрузки. Для этого выражение (2)
перепишем с учетом (1) в виде
P  I 2R 
Следовательно,
n 2 2 R
.
nr  R 2
nr  R   2 Rnr  R   0 ,
dP
 n 2 2
dR
nr  R 2
2
(3)
Откуда получаем
R  nr .
(4)
Из соотношения (3) с учетом (4) получаем
Pmax 
n 2 2 nr
n 2

 8,16 Вт .
nr  nr 2 4r
Задание 5.
этап
1
2
3
4
Содержание этапов
Записан закон сохранения энергии
mc2  E0  mc2  ( pc)2  E02
Здесь p, E0 – импульс и энергия покоя электрона
Записан закон сохранения импульса
mc  mc  p
Записана связь энергии с массой электрона
E0  me  c 2
Получен правильный ответ:
m
m 
m
1 2
me
Задание 6.
На протон при движении будут действовать сила Лоренца
FЛ  qv0 B
и сила электрического поля
Fэл  qE .

Уравнение движения протона вдоль нормали n к траектории и оси Z, параллельной
 
векторам E и B (см. рисунок.):
mv02
 FЛ , maz  Fэл
R
или
mv02
 qv0 B ,
R
maz  qE .
Рисунок к задаче
Составляющая скорости, перпендикулярная направлению полей, при движении частицы
не изменяется.
Вдоль оси Z протон будет двигаться с постоянным ускорением
az 
qE
,
m
И расстояние, пройденное им вдоль оси Z,
az t 2
s
.
2
Радиус R спирали и период T обращения соответственно равны
R
mv0
,
qB
T
2R 2m

.
v0
qB
Расстояния, пройденные протоном вдоль силовых линий за время первого и второго
оборотов:
azT 2 2 2mE
az (2T )2 azT 2 3  2 2mE
s1 

, s2 


.
2
qB 2
2
2
2qB 2
Эти расстояния равны соответствующим шагам витков. Поэтому
h2 s2
  3.
h1 s1