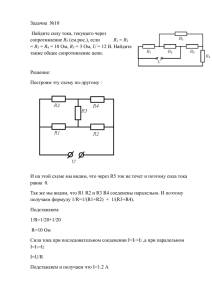
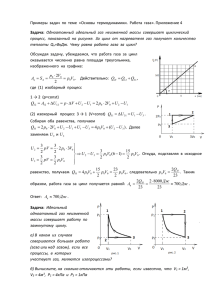
Задание 1. произведение векторов и и сравнивается с выражением в числителе

Задание 1. Вводя координаты точек А, В, С, D, вычисляется скалярное
произведение векторов AB и CD и сравнивается с выражением в числителе
дроби. Оказывается, что AB  CD    AD 2  BC 2  AC 2  BD 2  , откуда
1
2 

следует требуемое равенство.
Задание 2. Уравнение окружности радиуса R, проходящей через начало
координат (вершину параболы y 2  2 px ), имеет вид: ( x  R) 2  y 2  R 2 .
(Из соображений симметрии центр окружности должен находиться на оси
 y 2  2 px,
Ох). Решая систему уравнений 
2
2
2
( x  R)  y  R
с учетом того, что точка
(0, 0) должна быть единственной точкой пересечения (кратности 2), получаем
R = p.
Задание 3. Вычислить определитель любым способом, получается
выражение 1+ х, которое больше нуля при x > -1.
Задание 4. Вычисляя и сравнивая левую и правую части равенства, получаем
0 
2  α
 и множество
1  α 
 2
при α = -2 – единственное решение X  α  21  
1  a
b
 , где a, b  R .
решений при α = -1: X   
2 1  a b 
Задание 5. Пусть z  a  bi . Тогда, решая иррациональное неравенство
a 2  b  12  a 2  b  12  4 , приходим к неравенству
a2 b2

 1 , которое
3
4
на комплексной плоскости задает внутренность эллипса с центром в начале
координат и полуосями 3 и 2.
Задание 6. Вычисляя производную f (x) , получим выражение, которое
содержит 2014 слагаемых, причем 2013 из них содержат множитель x  2013 ,
который при подстановке вместо х числа 2013 обращается в ноль.
Единственное ненулевое слагаемое имеет вид: xx  1x  2...x  2012 , которое
при x  2013 равно 2013!.
x  xo y  y o z  z o
проходит


2 xo
4 yo
1
1  xo
y
2  zo
через точку М, то получаем
. Покажем, что yo  0 . Если
 o 
2 xo
4 yo
1
yo  0 , то получаем 1  xo   xo 2  xo  2, z o  7 4 , тогда
1  xo
7
2 y o2  z o  xo2   4  0 , что невозможно. Итак, yo  0 , тогда z o  2 
и
4
2 xo
Задание 7. Так как нормаль к поверхности
z o  xo2 , то есть xo находится из уравнения: 2 xo3  3 xo  1  0 . Корни уравнения:
x1  1, x 2 
1 3
1 3
, x3 
. Получаем три точки:
2
2

 

M1  1, 0,1, M 2 x2 ; 0; x22 , M 3 x3 ; 0; x32 . Проверкой убеждаемся, что
δ min  MM 2 
11  6 3
.
2
Задание 8. В задании была опечатка. За правильно вычисленный интеграл
выставлялся 1 балл.
Задание 9. Пусть график y  ( x ) пересекает ось Ох, т.е. y( x o )  ( x o )  0 .
Тогда единственное решение исходного уравнения в силу теоремы Коши
y( x)  0 . Действительно, правая часть уравнения и ее производная по у
непрерывны в окрестности любой точки ( x o , y o ) , в частности, и точки (хо, 0).
Задание 10. Пусть А – случайное событие, вероятность которого нужно
(1)
( 2)
найти. Тогда A  1  B1 2  D1 2  2 , где П – бактерия погибла на
первом или втором шаге, В – выжила, D – разделилась на две. П2(i) – погибает
i –я бактерия на втором шаге. Учитывая несовместность и независимость
событий, получим: Р(А) = 0,25 + 0,252 + 0,5·0,252 = 0,34375.