ОлимпМатем_6_7_8кл_13_решения

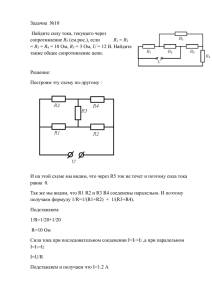
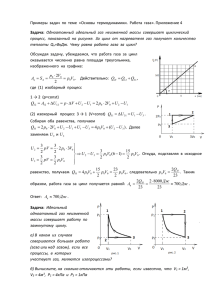
Напоминаем, что победители и призёры этой олимпиады 7 и 8 классов принимаются на
информационно-технологическое (профильные предметы программирование, математика) и
физико-математическое (профильные предметы физика, математика, астрономия) отделения
республиканского лицея без вступительных испытаний на основе собеседования, которое
состоится 26 мая по адресу ул.Попова, д.67 (остановка городского транспорта «Хлебозавод»
(«Горячий хлеб») на Юго-Западе). Результаты олимпиады находятся на сайте
www.edurm.ru
Решения.
6 класс
1. У отца шесть сыновей и одна дочь, то есть всего 7 детей.
2. Наливаем 5 литров во второй сосуд и переливаем из него в первый 3 литра, значит, в нем
останется 2 литра. Освобождаем 3-х литровый сосуд и наливаем в него полученные 2 литра. Опять
наливаем 5 литровый сосуд полностью и отливаем из него в 3-х литровый, но там уже есть 2 литра,
значит туда поместится только 1 литр, а в 5 литровом останется 4 литра.
3. В первый день гусеница достигнет высоты 6 см, затем ночью она вернётся на высоту 2 см. Во
второй день – 8 см, ночь – 4 см. Третий день – 10 см, ночь – 6 см. Четвертый день – 12 см, ночь – 8
см. Пятый день – 14 см. Ответ: на пятый день.
4. Запускаем одновременно эти часы, когда 7-минутные закончатся, то 11-минутным останется еще
4 минуты. В этот момент начинаем варить яйцо. Когда закончатся 11-минутные (значит, прошло 4
минуты), переворачиваем их, т.е. запускаем по-новому еще на 11 минут - итого получаем 15 минут.
5. Между полом первого этажа и полом третьего – два этажа, значит, лифт на один этаж тратит 3
секунды. Между полом первого этажа и полом пятого – четыре этажа, значит, лифт поднимется за
12 секунд.
6. Можно: в каждом углу нужно поставить по стулу и в центре каждой стены – тоже.
7. Полуметровых чурок получится 11 штук, значит, распилов будет 10, поэтому время равно 25
минут.
8. Если эти два землекопа будут работать в 50 раз дольше, т.е. 100 часов, то и сделают в 50 раз
больше, т.е. 100 метров. Ответ: два землекопа.
9. Если в большем классе удалить 6 учеников, то будет одинаковое количество, т.е. по (50-6)/2=22
человека. Значит, в меньшем классе 22 человека, а в большем 22+6=28 человек.
10. В первой строке количество букв в месяцах: январь – 6, февраль – 7, март -4 и т.д., а во второй –
количество дней в этом месяце в этом году.
6 7
4 6 3
4
31 28 31 30 31 30
7 класс
1. Сначала локомотив проезжает тоннель – это 0,5 км, затем из тоннеля выезжает весь поезд – это
еще 0,5 км. Значит всего 1 км, и если в час поезд проезжает 60 км, то за 1/60 часа он проедет 1 км.
Ответ: 1/60 часа или 1 минута.
2. 30 км/час – это 30 км за 60 минут, значит 1 км – в 30 раз меньше, т.е. 60/30=2 минуты. Значит,
второй километр ему можно не бежать – он уже опоздал!
3. Если из большей вазы удалить 12 конфет, то будет одинаковое количество, т.е. по (60-12)/2=24
конфеты. Значит, в меньшей вазе 24 конфеты, а в большей 24+12=36 конфет.
4. Всего кусков будет 200/20=10 штук, значит, разрезов будет 9. Поэтому последний разрез – 9
марта.
5. Начнем с того, что получилось: на берёзе вдвое больше (2 части), чем на осине (1 часть), а всего
48. Всего 3 части, на одну часть приходится 48/3=16. Поэтому на берёзе стало 32, а на осине 16.
Когда 5 птиц перелетели с берёзы на осину, а затем 12 птиц перелетели с осины на берёзу, то
получается, что реально с осины на берёзу перелетело 7 птиц. Вернем их назад – получим ответ: на
осине 16+7=23, а на берёзе – 32-7=25.
6. Если считать от 1 до 999, то это 999 чисел, но от 1 до 99 не трехзначные (99 штук) надо отнять,
остаётся 999-99=900 штук.
7. Когда собака сделает 4 скачка (это 8 метров), лиса сделает 6 скачков (это 6 метров), то есть,
собака приблизится на 2 метра. Это должно повториться 30/2=15 раз. Собака при этом пробежит
8*15=120 метров.
8. Проделаем все операции в обратном порядке: раз спичек не осталось, значит, их было 8. Но перед
этим их количество удвоили, значит, их было 4. Но эти 4 получились, когда перед этим отняли 8,
значит, было 12, но пред этим их удваивали, значит, было 6. И последний раз: 6 получилось, когда
забрали 8, значит, было 14, но их удваивали, значит было 7. Ответ: 7 спичек.
Построим каждую прямую по двум точкам: в первой при х=-1 y=3, а при х=1 y=2. У
второй прямой при х=1 y=2, при х=2 y=5. Получаем:
9.
10. В полночь стрелки совпали, сутки закончились, начинаем считать: почти сразу после 1 часа
минутная стрелка догонит часовую – они совпадут, после 2-х часов – опять, после 3-х, после 4-х и
так до того момента, когда они совпадут после 11 часов дня, но это получается ровно 12 дня. Всего
11 раз. И опять всё заново: еще 11 раз. Всего 22 раза.
8 класс
1. Если от цены книги отнять 60 копеек, то сама книга будет стоить столько же, сколько и переплет,
то есть (64-60)/2=2 копейки. Значит, сама книга стоит 60+2=62 копейки.
2. Запускаем одновременно эти часы, когда 7-минутные закончатся, то 9-минутным останется еще 2
минуты. В этот момент начинаем варить яйцо. Когда закончатся 9-минутные (значит, прошло 2
минуты), переворачиваем их, т.е. запускаем по-новому еще на 9 минут, а потом еще на 9 минут итого получаем 2+9+9=20 минут.
3. Пусть x брёвен по 3 метра и y брёвен по 4 метра, тогда получаем систему из двух уравнений:
 x  y  30,
. Решив эту систему, получаем x  20, y  10 . Для 3-х метрового бревна нужно

3x  4 y  100
2 распила, для 4-х метрового 3 распила, всего 20 * 2  10 * 3  70 распилов.
4. Обозначим y  x 2 , получим y  20  22  y . При 22  y  0 или y  22 получаем
y  20  484  44 y  y 2 или y 2  45 y  464  0 . Решив это квадратное уравнение, получаем
y1  16, y2  29 , но y  22 . Поэтому y  16, x  4 .
5. В 10 кг свежих огурцов 99% воды, значит сухого вещества там 1%, то есть 0,01*10=0,1 кг. При
хранении испаряется вода, а сухое вещество остается неизменным. Поэтому после неправильного
хранения воды стало 98%, а сухого вещества 2%. Если 0,1 кг – это 2%, то 100% в 50 раз больше, то
есть 50*0,1=5 кг. Ответ: 5 кг.
x  y  1  0
6. Решив систему 
, получаем x  4 , y  3 . Подставив эти значения в третье
7
7
2
x

5
y

1

0

уравнение, получаем верное равенство 4 * 4  3 * 3  1  0 , значит, точка лежит и на этой прямой.
7
7
Да, они все проходят через точку с координатами x  4 , y  3 .
7
7
7. Пусть x метров длина поезда, а v м/с – его скорость, тогда получаем систему уравнений:
x
 v  5,
. Решив её, получаем x  75, v  15 .

x

150

 15
 v
8. Пусть x кг весит первый раствор, а y кг – второй. Из условия задачи получаем
0,4 * x  0,55 * y
 0,5 . После преобразований y  2 * x . Значит, надо взять одну часть первого
x y
раствора и две части второго, то есть отношение 1:2.
1
1
9. Маша собирает в час корзинки ягод, а Петя в час корзинки ягод, значит, вместе они за час
2
3
1 1 5
5
60
1
 12 минут соберут   корзинки ягод. То есть за 60 минут корзинки, за
2 3 6
6
5
6
1
корзинки, а за 6 *12  72 минуты - 6 *  1 корзинку. Ответ: за 72 минуты.
6
10. Так как 20 мартышек получили по пинку, то они сорвали всего 20*3=60 фиников. Так как
произошло 30 новых пинков, значит, 30 мартышек съели по 2 финика (они то и пнули своих
соседей и это еще означает, что эти 60 фиников кончились), но те, что получили эти 30 пинков и
значит, сорвавшие 3*30=90 фиников, раздали их так, что новых пинков не последовало, значит, они
раздали их каждой по одному финику и поэтому их пока не съели. Получается, что осталось 90
фиников.