10 кл математика 1 четверть
реклама
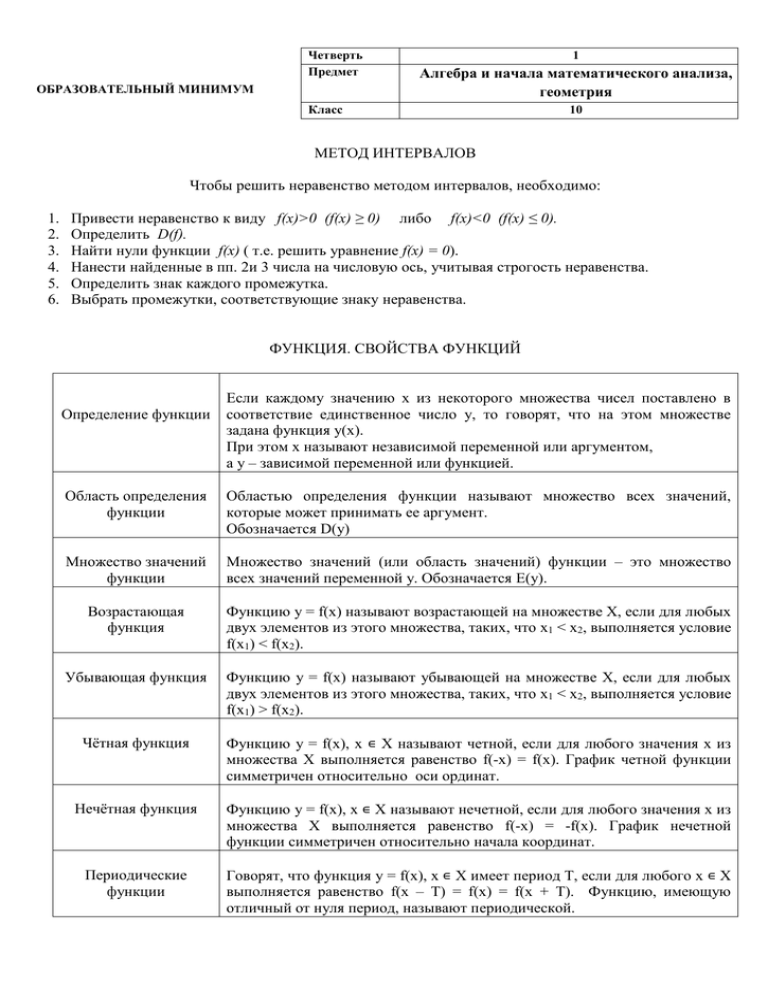
Четверть Предмет ОБРАЗОВАТЕЛЬНЫЙ МИНИМУМ 1 Алгебра и начала математического анализа, геометрия Класс 10 МЕТОД ИНТЕРВАЛОВ Чтобы решить неравенство методом интервалов, необходимо: 1. 2. 3. 4. 5. 6. Привести неравенство к виду f(x)>0 (f(x) ≥ 0) либо f(x)<0 (f(x) ≤ 0). Определить D(f). Найти нули функции f(x) ( т.е. решить уравнение f(x) = 0). Нанести найденные в пп. 2и 3 числа на числовую ось, учитывая строгость неравенства. Определить знак каждого промежутка. Выбрать промежутки, соответствующие знаку неравенства. ФУНКЦИЯ. СВОЙСТВА ФУНКЦИЙ Определение функции Если каждому значению х из некоторого множества чисел поставлено в соответствие единственное число у, то говорят, что на этом множестве задана функция у(х). При этом х называют независимой переменной или аргументом, а у – зависимой переменной или функцией. Область определения функции Областью определения функции называют множество всех значений, которые может принимать ее аргумент. Обозначается D(y) Множество значений функции Множество значений (или область значений) функции – это множество всех значений переменной у. Обозначается E(y). Возрастающая функция Функцию y = f(x) называют возрастающей на множестве Х, если для любых двух элементов из этого множества, таких, что х1 < x2, выполняется условие f(x1) < f(x2). Убывающая функция Функцию y = f(x) называют убывающей на множестве Х, если для любых двух элементов из этого множества, таких, что х1 < x2, выполняется условие f(x1) > f(x2). Чётная функция Функцию y = f(x), х ∊ Х называют четной, если для любого значения х из множества Х выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Нечётная функция Функцию y = f(x), х ∊ Х называют нечетной, если для любого значения х из множества Х выполняется равенство f(-x) = -f(x). График нечетной функции симметричен относительно начала координат. Периодические функции Говорят, что функция y = f(x), х ∊ Х имеет период Т, если для любого х ∊ Х выполняется равенство f(x – Т) = f(x) = f(x + T). Функцию, имеющую отличный от нуля период, называют периодической. Прямоугольный треугольник ФОРМУЛЫ ПЛОЩАДЕЙ Произвольный треугольник Квадрат Трапеция S a2 Прямоугольник Параллелограмм Круг Ромб R S ab S R 2 АКСИОМЫ СТЕРЕОМЕТРИИ А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. А3. Если две плоскости имеют точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. СЛЕДСТВИЯ ИЗ АКСИОМ С1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. С2. Через две пересекающиеся прямые проходит плоскость, и притом только одна. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ В ПРОСТРАНСТВЕ Если две параллельные прямые параллельны третьей, то они параллельны. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ Если прямая, не лежащая в плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости.