Уроки 15-16 Тема урока: «Медианы, биссектрисы и высоты треугольника.

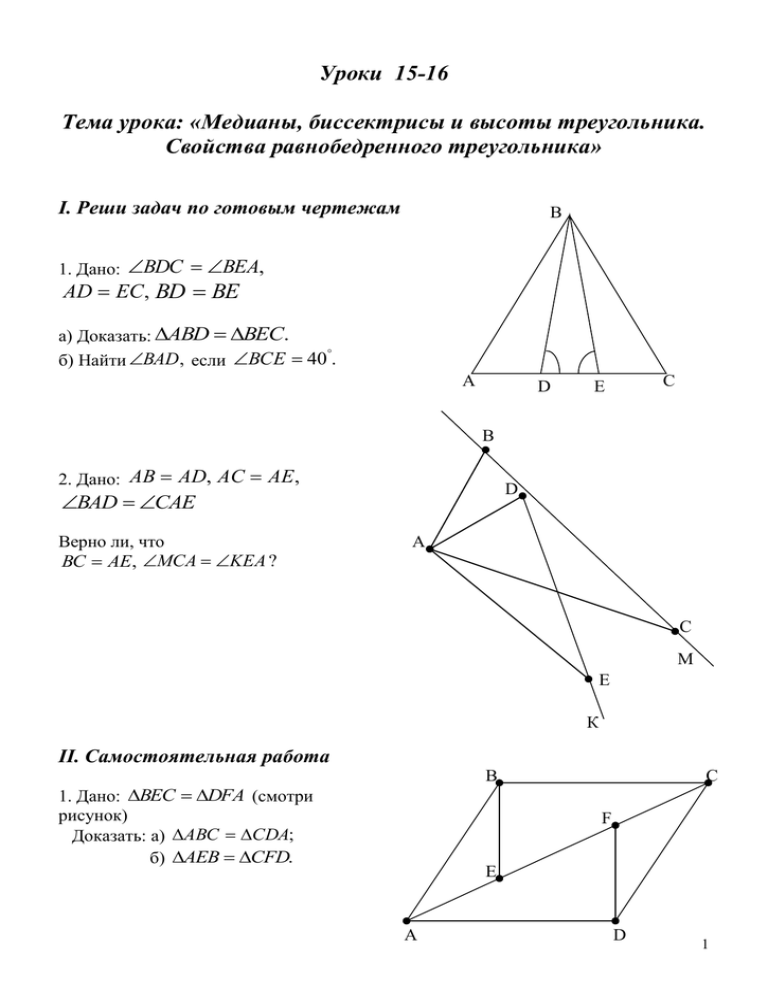
Уроки 15-16
Тема урока: «Медианы, биссектрисы и высоты треугольника.
Свойства равнобедренного треугольника»
I. Реши задач по готовым чертежам
B
1. Дано: BDC  BEA,
AD  EC, BD  BE
а) Доказать: ABD  BEC.

б) Найти BAD , если BCE  40 .
A
D
C
E
В
2. Дано: AB  AD, AC  AE ,
D
BAD  CAE
Верно ли, что
BC  AE, MCA  KEA ?
А
С
М
Е
К
II. Самостоятельная работа
B
1. Дано: BEC  DFA (смотри
рисунок)
Доказать: а) ABC  CDA;
б) AEB  CFD.
C
F
E
A
D
1
B
2. Дано: BO  OD, AO  OC (смотри
рисунок)
Сколько пар равных треугольников на
рисунке? Запишите все пары и
докажите равенство треугольников.
C
O
A
D
Решение задач самостоятельной работы
1. а) 1) BEC  DFA (по условию задачи)
 BC  AD, BE  FD, BCA  CAD, CBE  FDA.
2) BC  AD, BCA  CAD, AC  общая сторона  ABC  CDA (по двум
сторонам и углу между ними).
б) 1) ABC  CDA  AB  CD, ABC  CDA.
2) ABC  CDA, CBE  FDA, ABE  ABC  CBE ,
CDF  CDA  FDA  ABE  CDF.
3) AB  CD, BE  FD, ABE  CDF  AEB  CFD (по двум сторонам и
углу между ними).
2. BOC  DOA, BOA  DOC , ABC  CDA, ABD  CDB. Равенство
треугольников докажите самостоятельно.
III. Теоретические вопросы, изучаемые на уроке
1. Понятие перпендикуляра к прямой. Теорема о существовании и
единственности перпендикуляра к прямой, проходящего через данную точку.
2. Понятие медианы, биссектрисы и высоты треугольника. Свойства медиан,
биссектрис и высот треугольника (без доказательства).
3. Понятие равнобедренного треугольника. Понятие равностороннего
треугольника. Свойства равнобедренного треугольника.
Материал по рассматриваемым на уроках вопросам можно найти в учебной
литературе (ее список указан ниже):
[1]: глава II §2 (п.п.16-18).
IV. Практические задания
1. Начертите остроугольный, прямоугольный и тупоугольный треугольники.
С помощью масштабной линейки отметьте середины сторон и проведите медианы
в каждом треугольнике.
2. Начертите остроугольный, прямоугольный и тупоугольный треугольники.
С помощью линейки и транспортира проведите биссектрисы каждого
треугольника.
2
3. Начертите остроугольный, прямоугольный и тупоугольный треугольники.
С помощью чертежного угольника проведите высоты каждого треугольника.
Выводы из практических заданий:
1) Медианы треугольника пересекаются в одной точке. Точка пересечения
медиан треугольника находится внутри треугольника.
2) Биссектрисы треугольника пересекаются в одной точке. Точка пересечения
биссектрис треугольника находится внутри треугольника.
3) Высоты треугольника или их продолжения пересекаются в одной точке.
Точка пересечения высот или их продолжений в остроугольном треугольнике
находится внутри треугольника, в прямоугольном треугольнике совпадает с
вершиной прямого угла, в тупоугольном треугольнике находится за пределами
треугольника.
Эти утверждения нужно запомнить. Доказаны они будут в 8 классе.
V. Задачи для решения в классе по теме «Медианы, биссектрисы и
высоты треугольника. Свойства равнобедренного треугольника»
1. [1]: №109
Решение:
1) Так как по условию задачи AB  AC, то
P(ABC )  AB  AC  BC  2 AB  BC  32 см.
1
2) P(ABM )  AB  AM  MB  AB  AM  BC  24 см,
2
откуда 2 AB  2 AM  BC  48 см.
3) Так как 2 AB  BC  32 см и 2 AB  2 AM  BC  48 см, то
32  2 AM  48 см, AM  8 см.
Ответ: 8 см.
A
B
2. [1]: №110
Доказательство:
Пусть дан произвольный треугольник MNK , в
котором медиана MC является и высотой. Докажем, что
MN  MK . Это и будет означать, что треугольник MNK
равнобедренный.
Рассмотрим треугольники MNC и MKC.
NC  CK , MCN  MCK , MC  общая сторона.
Следовательно, NMC  KMC (по двум сторонам и углу
между ними).
Так как NMC  KMC , то MN  MK . Значит,
треугольник MNK равнобедренный, что и требовалось
доказать.
M
C
M
N
C
K
Итак, если медиана треугольника совпадает с его высотой, то он
является равнобедренным.
3
B
3. [1]: №114
Доказательство:
Пусть ABC  A1 B1C1 , BM и B1M1  медианы к
равным сторонам. Докажем, что BM  B1M1.
ABC  A1 B1C1  AB  A1 B1 , A  A1 , AC  A1C1.
AC  A1C1 , AM 
A
M
C
B1
1
1
AC , A1 M 1  A1C1  AM  A1 M 1 .
2
2
AM  A1M1 , AB  A1 B1 , A  A1  ABM  A1 B1M1 (по
двум сторонам и углу между ними)  BM  B1M1 , что и
требовалось доказать.
A1
M1
C1
Итак, в равных треугольниках медианы, проведенные к равным сторонам,
равны.
4. [1]: №116
Доказательство:
По условию задачи ABC равносторонний. Значит,
AB  BC  AC.
AB  BC  A  C (по свойству равнобедренного
треугольника).
AB  AC  B  C (по свойству равнобедренного
треугольника).
A  C , B  C  A  B  C , что и
требовалось доказать.
B
A
C
Итак, в равностороннем треугольнике все углы равны.
5. [1]: №119
Решение:
1) DEK  равнобедренный, EF  биссектриса, проведенная
к основанию. Следовательно, EF  медиана и высота
DEK (по свойству равнобедренного треугольника).
2) EF  медиана DEK  KF  0,5DK  0,5 16  8 см.
3) EF  высота DEK  EFD  90.
4) EF  биссектриса DEK  DEK  2DEF  2  43  86.
Ответ: 8 см; 86  ; 90 .
E
D
F
K
4
VI. Домашнее задание
1. Теория: [1]: глава II, §2, п.п. 16-18, вопросы 5-13.
2. Задачи: [1]: №104, №106, №113, №115, №117, №118.
Список литературы для учащихся:
1. Геометрия, 7-9: учебник для общеобразовательных учреждений/(Л. С. Атанасян,
В. Ф. Бутузов, С. Б. Кадомцев и др.). - 18-е изд. - М.: Просвещение, 2008.
2. Зив Б. Г. Геометрия: дидактические материалы для 7 класса/Б. Г. Зив, В. М.
Мейлер.-13-е изд. - М.: Просвещение, 2007.
5