Дистанционные уроки по геометрии 10 Б класс, 2 урока) Урок 1
реклама
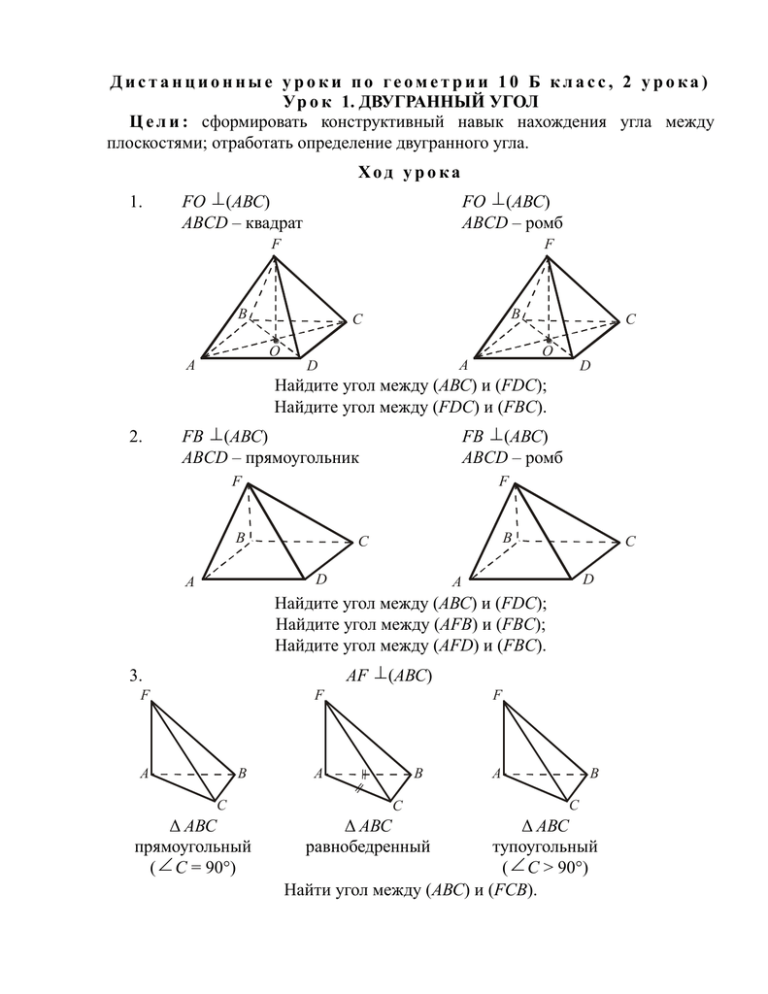
Дистанционные уроки по геометрии 10 Б класс, 2 урока) Ур о к 1. ДВУГРАННЫЙ УГОЛ Ц е л и : сформировать конструктивный навык нахождения угла между плоскостями; отработать определение двугранного угла. Ход у ро ка 1. FO (АВС) ABCD – квадрат FO (АВС) ABCD – ромб F F B B C O A C O A D D Найдите угол между (АВС) и (FDC); Найдите угол между (FDC) и (FBC). 2. FB (АВС) ABCD – прямоугольник FB (АВС) ABCD – ромб F F B B C D A C D A Найдите угол между (АВС) и (FDC); Найдите угол между (AFB) и (FBC); Найдите угол между (AFD) и (FBC). AF (АВС) 3. F F A B C Δ АВС прямоугольный ( С = 90°) F A B C Δ АВС равнобедренный A B C Δ АВС тупоугольный ( С > 90°) Найти угол между (АВС) и (FCВ). 4. ABCDEF – правильный шестиугольник SB (АВС). S B C D A F Найдите угол между: (ABS) и (СBS); (SFE) и (ABC); (ASF) и (ABC); (FSE) и (DSE); (FSE) и (BCS). E Решение задач: №№ 173, 176, 212, 213 (решите эту задачу, используя результат задачи № 212: SАВС = Sпр ∙ cos α), 214 (решите двумя способами). Ур о к 2. СВОЙСТВО ДВУГРАННОГО УГЛА Ц е л ь : доказать одно из свойств двугранного угла, часто применяющееся при решении задач. Ход у ро ка Если два плоских угла трехгранного угла равны, то их общее ребро проецируется на биссектрису третьего плоского угла. АВС АВD, Дано: = B ВО (АDС). Доказать, что АО – биссектриса САD. C Доказательство 2 A 1 1. Δ ABD = Δ АВС (как O прямоугольные по гипотенузе и D острому углу) AD = АС. 2. Δ ADO = Δ АСО (как прямоугольные по гипотенузе и катету) 1 = 2 АО – биссектриса. I. Решение задач. № 1. Все грани параллелепипеда – равные ромбы, со стороной а и острым углом α. Найдите высоту параллелепипеда. Решение B1 C1 D1 A1 B C O M A D А1 АD А1 АВ O A O ( ADC ) 1. 1 биссектрисе А. ABCD ромб O AC. O биссектрисе A 2. 3. Проведем ОМ AD. По теореме о трех перпендикулярах А1М AD. 4. Δ АА1М – прямоугольный. AM = a ∙ cos α. AM a cos α α α cos cos 2 2 . 5. Δ АОМ – прямоугольный. АО = 6. Δ А1АО – прямоугольный. AA12 AO 2 a 2 a cos α 2 α cos 2 2 2 α cos 2 α 2 α cos 2 . a cos 2 H = А1О = № 2. Основанием параллелепипеда является прямоугольник со сторонами а и b. Боковое ребро длины с образует со смежными сторонами основания углы, равные φ. Найдите высоту параллелепипеда. Решение B1 C1 D1 A1 K b B c O A M C a D А1 АD А1 АВ O A O ( ABD ) 1. 1 биссектрисе А. АK биссектриса А O AK . ВАK DAK 45 2. 3. Проведем ОМ AD. По теореме о трех перпендикулярах А1М AD. 4. Δ А1АМ – прямоугольный. AM = c ∙ cos φ. АМ 2 cos 45 5. Δ АОМ – прямоугольный. АО = ∙ c ∙ cos φ. 6. Δ А1АО – прямоугольный. H = c cos 2 . А1О 2 2 2 2 2 2 AA AO c 2 c cos c 1 2cos 1 = № 3. Все грани тетраэдра АBCD – равные равнобедренные треугольники с боковыми сторонами, равными а, и углом между ними – 2α. Найдите высоту тетраэдра. Решение D 2α 2α A B O M 2α K DAC DAB O DO ( ABC ) 1. биссектрисе А. АВС равнобедренный АK биссектриса 2. AK – медиана и высота. О АK. 3. Δ MDC – прямоугольный. DM = a ∙ sin 2α. MC = a ∙ cos 2α. 4. AM = AC – MC = a – a ∙ cos 2α = a (1 – cos 2α) = 2a sin2α. 5. Δ AOM – прямоугольный. OM = AM ∙ tg α = 2a sin2α ∙ tg α. C 6. H = DO 2 2 2 2 2 4 2 = DM OM a sin 2α 4a sin α tg α 2 2 2 = 2a sin α cos α sin α tg α 2a tg α cos 2α . Домашнее задание: №№ 174, 175, 216.