вариант 4 - 2015x (84290)

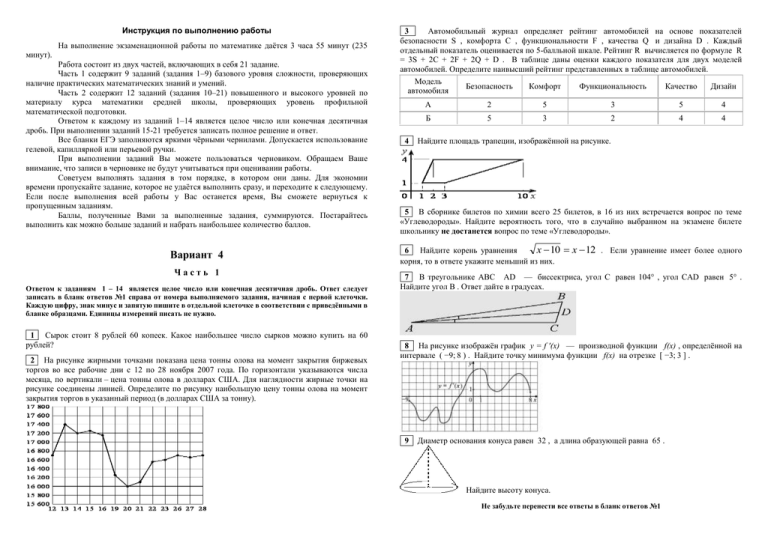
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике даётся 3 часа 55 минут (235
минут).
Работа состоит из двух частей, включающих в себя 21 задание.
Часть 1 содержит 9 заданий (задания 1–9) базового уровня сложности, проверяющих
наличие практических математических знаний и умений.
Часть 2 содержит 12 заданий (задания 10–21) повышенного и высокого уровней по
материалу курса математики средней школы, проверяющих уровень профильной
математической подготовки.
Ответом к каждому из заданий 1–14 является целое число или конечная десятичная
дробь. При выполнении заданий 15-21 требуется записать полное решение и ответ.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование
гелевой, капиллярной или перьевой ручки.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше
внимание, что записи в черновике не будут учитываться при оценивании работы.
Советуем выполнять задания в том порядке, в котором они даны. Для экономии
времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему.
Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к
пропущенным заданиям.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь
выполнить как можно больше заданий и набрать наибольшее количество баллов.
Вариант 4
Часть 1
Ответом к заданиям 1 – 14 является целое число или конечная десятичная дробь. Ответ следует
записать в бланк ответов №1 справа от номера выполняемого задания, начиная с первой клеточки.
Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в
бланке образцами. Единицы измерений писать не нужно.
1 Сырок стоит 8 рублей 60 копеек. Какое наибольшее число сырков можно купить на 60
рублей?
2 На рисунке жирными точками показана цена тонны олова на момент закрытия биржевых
торгов во все рабочие дни с 12 по 28 ноября 2007 года. По горизонтали указываются числа
месяца, по вертикали – цена тонны олова в долларах США. Для наглядности жирные точки на
рисунке соединены линией. Определите по рисунку наибольшую цену тонны олова на момент
закрытия торгов в указанный период (в долларах США за тонну).
3
Автомобильный журнал определяет рейтинг автомобилей на основе показателей
безопасности S , комфорта C , функциональности F , качества Q и дизайна D . Каждый
отдельный показатель оценивается по 5-балльной шкале. Рейтинг R вычисляется по формуле R
= 3S + 2C + 2F + 2Q + D . В таблице даны оценки каждого показателя для двух моделей
автомобилей. Определите наивысший рейтинг представленных в таблице автомобилей.
Модель
Безопасность
Комфорт
Функциональность
Качество
Дизайн
автомобиля
4
А
2
5
3
5
4
Б
5
3
2
4
4
Найдите площадь трапеции, изображённой на рисунке.
5 В сборнике билетов по химии всего 25 билетов, в 16 из них встречается вопрос по теме
«Углеводороды». Найдите вероятность того, что в случайно выбранном на экзамене билете
школьнику не достанется вопрос по теме «Углеводороды».
6 Найдите корень уравнения
х  10
корня, то в ответе укажите меньший из них.
 x  12 . Если уравнение имеет более одного
7 В треугольнике ABC AD — биссектриса, угол C равен 104° , угол CAD равен 5° .
Найдите угол B . Ответ дайте в градусах.
8 На рисунке изображён график y = f '(x) — производной функции f(x) , определённой на
интервале ( −9; 8 ) . Найдите точку минимума функции f(x) на отрезке [ −3; 3 ] .
9
Диаметр основания конуса равен 32 , а длина образующей равна 65 .
Найдите высоту конуса.
Не забудьте перенести все ответы в бланк ответов №1
Часть 2
10
Найдите значение выражения
48  ctg
17
13
7
.
 cos
4
6
Решите неравенство
2 | 2  x |
x .
18 Две окружности с центрами О1 и О2 касаются друг друга внутренним образом. Третья
окружность, с центром в точке О, касается первых двух и прямой О1О2.
11 Для одного из предприятий-монополистов зависимость объёма спроса на продукцию q
(единиц в месяц) от её цены p (тыс. руб.) задаётся формулой: q  110  p . Определите
а) Докажите, что периметр треугольника ОО1О2 равен наибольшему из диаметров этих трёх
окружностей.
минимальный уровень цены p (в тыс. руб.), при котором значение выручки предприятия за
месяц r  q  p составит не менее 3000 тыс. руб.
б) Найдите диаметр третьей окружности, если диаметры первых двух равны 2 и 8 .
12 Найдите площадь боковой поверхности многогранника, вершинами которого являются
точки С , D , E , F , D1 , E1 , F1 , С1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 ,
сторона основания которой равна 3 , а боковое ребро равно 5 .
19 1 января 2014 года Василий Васильевич взял в банке некоторую сумму рублей в кредит
под некоторый процент годовых. Схема выплаты кредита такова: 1-го января каждого
следующего года банк начисляет х% на оставшуюся сумму долга (то есть увеличивает долг на
х процентов), затем Василий Васильевич переводит в банк очередной ежегодный платёж. Если
он будет платить каждый год по 656100 рублей, то выплатит долг за четыре года. Если же он
будет платить каждый год по 1174500 рублей, то выплатит долг за два года. Под какой процент
годовых Василий Васильевич взял деньги в банке?
20
13 По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и
пассажирский поезда, скорости которых равны соответственно 60 км/ч и 40 км/ч. Длина
пассажирского поезда равна 300 метрам. Найдите длину скорого поезда, если время, за которое
он прошел мимо пассажирского поезда, равно 18 секундам. Ответ дайте в метрах.
14 Найдите точку минимума функции
y
x
x  289
2
.
Не забудьте перенести все ответы в бланк ответов №1
Для записи решений и ответов на задания 15 – 21 используйте бланк ответов №2.
Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и
ответ. Ответы записывайте чётко и разборчиво.
15 а) Решите уравнение
2 cos 3 x  2 cos x  sin 2 x .
б) Найдите все корни этого уравнения, принадлежащие отрезку
 3

  2 , 0 .


16 В треугольной пирамиде ТАВС с вершиной Т и основанием АВС высоты ТМ , ТК и
ТР боковых граней пирамиды равны между собой, при этом точки М , К и Р лежат на
сторонах треугольника АВС . Точка Н – проекция вершины Т на основание АВС .
а) Докажите, что Н – центр вписанной окружности треугольника АВС .
б) Найдите ТМ , если ТН = 5 , площадь основания АВС равна 24 ,
и периметр основания АВС равен 24 .
Найдите все значения параметра
неравенства


а , при каждом из которых множество решений
a  4  29  2a  3a cos x
1
sin 2 x  a 2  1`
2
содержит отрезок
  
3 , 2 .


21 По окружности расставляют 48 ненулевых целых чисел с общей суммой 20 . При этом
любые два стоящих рядом числа должны отличаться не более чем на 7 и среди любых четырёх
подряд идущих чисел должно быть хотя бы одно положительное.
а) Среди таких 48 чисел найдите наибольшее возможное количество положительных.
б) Среди таких 48 чисел найдите наименьшее возможное количество положительных.