МЕТОДИЧЕСКОЕ ПОСОБИЕ для кадет
реклама

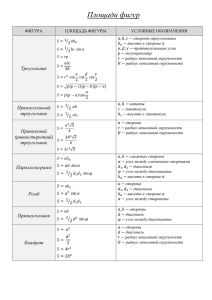
В ОЕННО - ТЕХНИЧЕСКИЙ КАДЕТСКИЙ КОРПУС Дисциплина: «Математика, основы информатики и вычислительной техники» МЕТОДИЧЕСКОЕ ПОСОБИЕ для кадет Сборник задач по геометрии с решениями для подготовки кадет к математической олимпиаде среди обучающихся суворовских военных, Нахимовского военно-морского училищ и кадетских корпусов Министерства обороны Российской Федерации г. Тольятти 2004 г. Тема: Сборник задач по геометрии с решениями для подготовки кадет класса к математической олимпиаде среди обучающихся суворовских военных, Нахимовского военно-морского училищ и кадетских корпусов Министерства обороны Российской Федерации. Учебные цели: Данное методическое пособие предназначено для тщательной подготовки кадет к математической олимпиаде среди обучающихся суворовских военных, Нахимовского военно-морского училищ и кадетских корпусов Министерства обороны Российской Федерации. Учебные вопросы: 1. Планиметрия. 1.1. Формулы планиметрии. 1.2. Задачи с решениями. 1.3. Задачи для самостоятельного решения. 2. Стереометрия. 1.1. Формулы стереометрии. 1.2. Задачи с решениями. 1.3. Задачи для самостоятельного решения. Данное методическое пособие предложено для кадет, проявляющих интерес к изучению геометрии. По форме изложения пособие представляет собой практикум по решению задач: каждый параграф содержит справочный материал по формулам, общие рекомендации по решению задач этого параграфа и решение этих задач. Вместе с тем он является и сборником задач: в конце каждого параграфа помещены задачи для самостоятельного решения с ответами. Так как решение большинства стереометрических задач сводится к решению задач планиметрических, то целесообразно системно повторить курс планиметрии посредством решения задач различной степени сложности по таким основополагающим разделам планиметрии, как «Треугольники», «Четырехугольники», «Окружность и круг». Алгоритмов решения геометрических задач, как правило, нет. Удачный же выбор в каждом конкретном случае подходящей теоремы (формулы) достигается путем решения достаточно большого количества задач. ФОРМУЛЫ ПЛАНИМЕТРИИ Треугольник Содержание формулы Периметр (Р) Формула P a b c; abc p 2 Сумма внутренних углов A B C 180 Символы (обозначения) a, b, c - длины сторон р - полупериметр A, B, C - величины углов a 2 b 2 c 2 2bc cos A; b 2 a 2 c 2 2ac cos B; Теорема косинусов Теорема синусов Радиус описанной окружности Площадь (S) Формула Герона Связь между медианой и сторонами Свойство биссектрисы внутреннего угла Связь между высотами и радиусом вписанной окружности c 2 a 2 b 2 2ab cos C ; b2 c2 a2 cos A 2bc a b c sin A sin B sin C a b c 2R sin A sin B sin C 1 1 1 S aha bhb chc ; 2 2 2 1 1 S ab sin C ac sin B 2 2 1 bc sin A; S pr, 2 abc S 4R S p ( p a )( p b)( p c) ma2 2b 2 2c 2 a 2 4 m a n b 1 1 1 1 ha hb hc r a, b, c - длины сторон A, B, C - величины углов R - радиус описанной окружности a, b, c – длины сторон ha , hb , hc – длины высот A, B, C – величины углов р – полупериметр r – радиус вписанной окружности R – радиус описанной окружности a, b, c – длины сторон m a – длина медианы к стороне а m, n – длины отрезков, на которые биссектриса угла С делит сторону с ha , hb , hc – длины высот r – радиус вписанной окружности Прямоугольный треугольник Содержание формулы Метрические соотношения Зависимость между сторонами, радиусами вписанной и описанной окружности Площадь (S) a 2 c a1 , b 2 c b1 c abc R ;r ; 2 2 a, b – длины катетов с – длина гипотенузы hc длина высоты a1 , b1 длины проекций катетов на гипотенузу r – радиус вписанной окружности R – радиус описанной окружности a b a2 b2 r ; 2 1 R r ( a b) 2 1 S ab a, b – длины катетов 2 Правильный треугольник Символы Формула Периметр (Р) P 3a Величина угла A B C 60 Зависимость между высотой и стороной Выражение площади (S) через: сторону, радиус описанной окружности, радиус вписанной окружности А, В – величины острых углов a2 b2 c2 hc2 a1 b1 ; Содержание формулы Зависимость между стороной, радиусами вписанной и описанной окружностей (обозначения) А В 90 Сумма острых углов Теорема Пифагора Символы Формула h a – длина стороны A, B, C – величины углов a 3 2 a R 3; R 2 r ; R r (обозначения) a 3 6 a2 3 S ; 4 3R 2 3 S ; 4 S 3r 2 3 a 3 3 h длина высоты a – длина стороны R – радиус описанной окружности r – радиус вписанной окружности a – длина стороны R – радиус описанной окружности r – радиус вписанной окружности Четырехугольник Содержание формулы Формула Сумма углов Свойство сумм величин противоположных углов вписанного четырехугольника Свойство сумм длин противоположных сторон описанного четырехугольника Теорема Птолемея A B C D 360 Площадь (S) A C B D 180 acbd mn ac bd 1 S mn sin ; 2 S pr Символы (обозначения) A, B, C , D – величины углов A, С и В, D – величины пар противоположных углов a, c и b, d – длины пар противоположных сторон m, n – длины диагоналей m, n – длины диагоналей – величина угла между ними р – полупериметр r – радиус вписанной окружности Параллелограмм Содержание формулы Формула Периметр (Р) Соотношение между квадратами длин сторон и диагоналей P 2(a b) m 2 n 2 2 (a 2 b 2 ) S a ha b hb ; Площадь (S) Свойства углов S ab sin B; 1 S mn sin 2 A B C D 360 ; A C; В D ; A B В С 180 Символы (обозначения) a, b – длины сторон m, n – длины диагоналей ha , hb – длины высот В – величина угла между сторонами – величина угла между диагоналями A, B, C , D – величины углов Прямоугольник Содержание формулы Формула Периметр (Р) P 2(a b) Площадь (S) S a b; 1 S d 2 sin 2 Символы (обозначения) a, b – длины сторон d – длина диагонали – величина угла между диагоналями Ромб Содержание формулы Периметр (Р) Формула P 4a S (обозначения) a – длина стороны h – длина высоты m, n – длины диагоналей S a h; Площадь (S) Символы 1 mn 2 Квадрат Содержание формулы Углы Связь между длиной стороны и радиусом описанной окружности Связь между длиной стороны и радиусом вписанной окружности Площадь (S) Содержание формулы Свойство средней линии Площадь (S) Формула A B C D 90 a R 2; R a 2 2 a r ; a 2r 2 Символы (обозначения) A, B, C , D – величины углов a – длина стороны R – радиус описанной окружности r – радиус вписанной окружности S a2; S 2R 2 Трапеция Формула ab 2 ab S h; 2 S mh m Символы (обозначения) m – длина средней линии a, b – длины оснований h – длина высоты Правильный многоугольник Содержание формулы Сумма внутренних углов () Формула A 1 a r n; 2 1 360 S R 2 n sin 2 n S Площадь (S) (обозначения) (n 2) 180 180 (n 2) n 180 a n 2r tg ; n Связь между длиной an стороны и радиусом r вписанной окружности 180 2tg n Связь между длиной a 2 R sin 180 ; n n стороны и радиусом описанной окружности a 3 R 3; a 4 R 2 ; a 6 R Угол Символы п – число сторон A – величина угла aп – длина стороны r – радиус вписанной окружности R – радиус описанной окружности a – длина стороны п – число сторон r – радиус вписанной окружности R – радиус описанной окружности Окружность и круг Содержание формулы Формула Длина окружности (С) C 2R Rn l ; l R 180 d 2 S R 2 ; S 4 2 R n S 360 Длина дуги (l) Площадь круга (S) Площадь сектора (S) Символы (обозначения) С – длина окружности R – радиус окружности п – градусная мера дуги - радианная мера дуги R – радиус круга d – диаметр b –основание сегмента S Площадь сегмента (S) R2n 360 2 S bh 3 S ; h – высота сегмента ЗАДАЧИ С РЕШЕНИЯМИ Задача 1. Площадь треугольника АВС равна 30 см2. На стороне АС взята точка D так, что AD : DC = 2 : 3. Длина перпендикуляра DE , проведенного на сторону ВС, равна 9 см. Найти ВС. Решение Проведем BD; В треугольни Е ки ABD и BDC имеют общую А С высоту BF; F D следователь С другой стороны, согласно формулы площади треугольника, но, их 1 1 площади S BDC BC DE или 18 = BC 9 , откуда ВС = 4 см. относятся 2 2 как длины Ответ: ВС = 4 см. оснований, т.е. Задача 2. В равнобедренном треугольнике проведенные к SΔABD : SΔBDC =высоты, 2 : 3, откуда основанию и к боковой стороне, равны соответственно 10 и2 12 см. Найти SΔBDC = SΔABС = 18 см . длину основания. Решение В В треугольнике АВС имеем АВ=ВС, BDAC, АЕВС, BD = 10 см и АЕ = 12 см. Е Пусть АС = х, АВ = ВС = у. Прямоугольные треугольники АЕС и BDC подобны (угол С – А С D общий); следовательно, ВС : АС = BD : АЕ или у : х = 10 : 12 = 5 : 6. Применяя теорему Пифагора к треугольнику BDC, имеем x2 ВС BD DC , т.е. y 100 . Решив систему уравнений 4 2 2 2 2 y 5 x 6 , 2 y 2 100 x , 4 получим х = 15. Итак, АС = 15 см. Ответ: АС = 15 см. Задача 3. Две окружности касаются внешним образом. К первой из них проведена касательная, проходящая через центр второй окружности. Расстояние от точки касания до центра второй окружности равно утроенному радиусу этой окружности. Во сколько раз длина первой окружности больше длины второй окружности? Решение Пусть О1 и О2 – центры окружностей, А – точка касания. Тогда О1А = R1, О1О2 = R1 + R2, О1А = 3R2 (по условию). Требуется найти отношение 2R1 : 2R2 = R1 : R2. В прямоугольном треугольнике О1АО2 (А = 90о) имеем О1О2 2 О1 А 2 О2 А 2 или (R1 + R2)2 = R12 + (3R2)2. Упростив это равенство, получим R1 = 4R2, откуда R1 : R2 = 4. Ответ: в 4 раза. Задача 4. Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки длиной m и n. Доказать, что площадь треугольника S = mn. Найти площадь прямоугольника, вписанного в данный треугольник так, что одна его вершина совпадает с вершиной прямого угла, а противоположная вершина – с точкой касания окружности и гипотенузы. Решение Пусть D, E, F – точки касания; тогда AD = AF = m, BD = BE = n, CE = CF =r – радиус вписанной окружности, p=r+m+n – полупериметр. формулу Тогда, площади прямоугольного треугольника, находим S или используя 2S r 2 r (m n) mn r (r m n) mn rp mn . (r m)(r n) 2 Из формулы площади треугольника rp = S, 2S = S + mn, окуда S = mn. Пусть CMDK – вписанный прямоугольник. Так как DK||BC, то используя гомотетию с центром в А и коэффициентом k m , найдем mn площадь S1 треугольника ADK: S1 S ABC m2 ( m n) 2 m3n ( m n) 2 . Аналогично для площади S2 треугольника BDM имеем S 2 S ABC n2 ( m n) 2 mn 3 ( m n) 2 . Искомая площадь S CMDK mn Ответ: 2m 2 n 2 ( m n) 2 m 3 n mn 3 ( m n) 2 2m 2 n 2 ( m n) 2 . . Задача 5. В прямоугольном треугольнике проведена биссектриса острого угла; отрезок, соединяющий ее основание с точкой пересечения медиан, перпендикулярен катету. Найти углы треугольника. Решение А Пусть ВЕ – медиана, О – точка пересечения медиан, AD – биссектриса, E O ODВС. Согласно свойству точки пересечения C D B медиан, ЕО : ОВ = 1 : 2. Так как OD||ЕC, то по теореме Фалеса CD : DB = EO : OB = 1 : 2. Используя свойство биссектрисы треугольника, получаем CD : DB = АС : АB, т.е. АС : АB = 1 : 2. Следовательно, sinB = 1/2, откуда В = 30о, А = 60о. Ответ: 90о, 30о, 60о. Задача 6. В треугольник ABC вписан параллелограмм ADEF так, что угол А у них общий, а вершина Е лежит на стороне ВС. Площадь параллелограмма равна 36 см2, а треугольника BDE – 24 см2. Найдите площадь треугольника ABC. Решение В Обозначим площади треугольников h1 D KL E ABC, DВE, DFE соответственно S, S1, h h2 A H F S2, а их высоты – ВН = h, ВK = h1, FL = C h2. Из подобия треугольников ABC и DВE (DE || AC) следует, что отношение площадей этих треугольников равно 2 h S h квадрату отношения их высот: . . Найдем отношение h1 S1 h1 Треугольники DВE и DFE имеют общее основание DE, поэтому отношение S1 : S2 площадей этих треугольников равно отношению h1 : h2 их высот : S1 : S2 = h1 : h2. Учитывая, что S1 = 24, S 2 S DFE получаем 24 : 18 = h1 : h2, значит, h2 3 h1 . 4 1 S ADEF 18 , 2 3 7 h1 = h1 . 4 4 Следовательно, h1 : h2 = 7:4. Тогда S : S1 = 49 : 16, откуда 49 49 S S1 24 73,5 (см.2). 16 16 Ответ:73,5 см2. Поэтому h BH BK KH h1 h2 h1 Задача 7. Две стороны треугольника равны соответственно 6 и 8. Медианы, проведенные к этим сторонам, пересекаются под прямым углом. Найдите третью сторону треугольника. Решение В Пусть АС = 6, ВС = 8, и медианы АЕ и BD пересекаются под прямым углом в точке М. М Найдем длину стороны АВ. А Е Так как М – точка пересечения медиан АЕ и BD треугольника АВС, то ВM : MD AM : ME 2 : 1 . Поэтому, если D МЕ = а, MD = b, то АМ = =2а, ВМ = 2b. C По теореме Пифагора в прямоугольных треугольниках АМD и ВМЕ имеем: AM 2 DM 2 AD 2 , EM 2 BM 2 BE 2 . Учитывая, что AD 1 1 AC 3, BE BC 4 , получаем 2 2 4a 2 b 2 9, 2 a 4b 2 16. Cложив эти равенства, находим a 2 b 2 5 . В прямоугольном треугольнике АМВ AB 2 AM 2 BM 2 4 a 2 b 2 = 4 5 20 , откуда AB 2 5 . Ответ: 2 5 . Задача 8. В равнобедренном треугольнике АВС (АВ = АС) на стороне ВС взята точка М так, что ВМ : МС = 1 : 4. В каком отношении прямая АМ делит медиану ВЕ треугольника АВС, считая от вершины В? Решение Проведем EF || AM, F MC . Тогда EF – В М К средняя линия треугольника АМС F – середина МС. Поэтому ВМ : МС = 1 : 4, MF : MC = 1 : 2, F откуда ВМ : MF = 1 : 2, значит, ВМ : ВF =1 : 3. А По теореме Фалеса ВК : ВЕ = ВМ : ВF = 1 : 3, С E следовательно, ВК : КЕ = 1 : 2. Ответ: 1 : 2. Задача 9. В равнобедренный треугольник АВС (АВ = ВС) вписана окружность, которая касается сторон АС и ВС соответственно в точках D и E; проведены отрезки DF и EK, параллельные стороне AB (FBC, KAC). Найдите длину стороны ВС, если EF = a, KD = b. Решение В Пусть CD = х. Тогда СК = CD – KD = x – b, CE = CD = x (как отрезки F E касательных), CF = CE + EF = x + a. Из подобия треугольников СКЕ и A D K C CDF следует: СК : CD = CE : CF или ( x b) : x x : ( x a) , откуда находим x ab . ab ab a2 a Тогда CF . А такт как DF || AB и точка D – ab ab середина АС, то DF – средняя линия треугольника АВС. Значит, F – 2a 2 середина ВС и BC 2CF ab 2a 2 Ответ: . ab Задача 10. В выпуклом четырехугольнике ABCD через середину диагонали BD проведена прямая, параллельная диагонали АС. Эта прямая пересекает сторону AD в точке Е. Докажите, что прямая СЕ разбивает четырехугольник ABCD на две равновеликие части. Решение В Пусть K – середина диагонали BD, P – точка пересечения данной прямой со стороной CD четырехугольника ABCD. Тогда S ACE S ACM , где М – произвольная точка А С прямой РЕ. Значит, S ABCE S ABCM . Возьмем в качестве М точку К – середину диагонали BD. Е К Р D Тогда S ABCE S ABCK 1 BK AC sin , где 2 диагоналями данного четырехугольника. Так как S ABCK – угол BK между 1 BD , то 2 1 1 1 1 BD AC sin S ABCD . Значит, S ABCE S ABCD , что и 2 2 2 2 требовалось доказать. Задача 11. Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD = = 3RD. Прямые AR и RD пересекаются в точке Q. Найдите площадь треугольника APQ, если AD = 2 BC. Решение B C M Достроим L P ABCD параллелограмма ABМD. Тогда R до BМ = =AD = 2 ВС С – середина BМ. Значит, Q A трапецию D СР || АМ. Пусть L AM BD (в параллелограмме ABMD). Из этого следует, что L – середина BD. Тогда DC и ML – медианы треугольника BMD; точка пересечения этих медиан делит каждую из них в отношении 2 : 1, считая от вершины. Но отрезок СD в отношении 2 : 1 делит точка R (2CD = 3RD DR : CD = 2 : 3 DR : RC = 2 : 1). Это означает, что точка R принадлежит диагонали АМ параллелограмма ABMD, т. е. точки L и M лежат на прямой AR. Но точка Q AR PD также лежит на прямой AR, т. е. точки Q,, L, R лежат на диагонали АМ. Далее, CR : CD = 1 : 3, CP || AM CR : CD = PQ : PD =1 : 3 S APD 3 S APQ . Кроме того, треугольники ABD и BCD имеют общую высоту (равную высоте трапеции) и AD = 2ВС, поэтому S ABD 2S BCD . А так как S ABD S BCD 30 , то 3S BCD 30 , откуда S BCD 10, S ABD 20 . Поскольку точка Р – середина АВ, то S APD что S APD 3 S APQ , получаем S APQ Ответ: 1 S ABD 10 . Учитывая, 2 10 (кв. ед.) 3 10 (кв. ед.). 3 Задача 12. Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность. Площадь описанного круга в 12 раз больше площади вписанного круга. Найдите углы трапеции. Решение (первый способ) В С Обозначим: AD a, BC b, AB CD c, CE h (высота трапеции); R – радиус описанной окружности, О О1 r – радиус вписанной окружности. Тогда А E D 2 2 2 S впис.кр. r , R 12r R 2r 3 S опис.кр. 12 S впис.кр. S опис.кр. R 2 , (1) Далее выразим дважды длину диагонали АС через r и , где ADC . Имеем, с одной стороны, в ACD AC 2 R . Учитывая (1), получаем sin AC 2R sin 4r sin 3 . (*) С другой стороны, АСE (АЕС 90) по теореме Пифагора: AC 2 AE 2 EC 2 . (**) Выразим АЕ и ЕС через r и . Трапеция ABCD описана около окружности радиуса r, поэтому высота ЕС 2r и a b 2c , откуда c ab . Таким образом, АЕ = с. 2 В прямоугольном треугольнике DEC находим: с CD Следовательно, AE c 2r . Подставив в (**) вместо АЕ и ЕС их sin найденные значения, получаем AC CE 2r . sin sin 2r 1 sin 2 sin (***) 2r 1 sin 2 Из (*) и (**) имеем 4r 3 sin или sin 12 sin 4 sin 2 1 0, sin 0. Сделав подстановку sin 2 t (t 0) , приходим к уравнению 1 12t 2 t 1 0 , корнями которого являются t1 (не удовлетворяют 4 1 условию t 0 ) и t 2 . Тогда 3 1 sin (не удовлетворяет условию, т. к. 90), 1 3 2 sin 1 3 sin 3 . Итак, sin A D arcsin 1 , откуда arcsin 3 1 3 1 3 . Таким образом, , следовательно, B C arcsin Ответ: arcsin 1 3 ; arcsin 1 3 1 3 . . Решение (второй способ) Выразим дважды площадь трапеции через r и . Имеем, S трап. AD BC ab CE h. 2 2 С одной стороны, в трапеции ABCD, описанной около окружности радиуса r, имеют место ECD c ab c, h 2r , а в прямоугольном треугольнике 2 h . Поэтому sin S трап. ab h2 4r 2 hch 2 sin sin (2) С другой стороны, ab AE (трапеция ABCD – равнобедренная). 2 Найдем АЕ. ACE (E 90) : по теореме Пифагора AE AC 2 CE 2 . ACD : AC 2R sin . Учитывая, что R 2r 3 , получаем AE 4R 2 sin 2 (2r ) 2 2r 12 sin 2 1 . Тогда S трап. AE CE 2r 12 sin 2 1 2r 4r 2 12 sin 2 1 . (3) 4r 2 Из (2) и (3) получаем 4r 12 sin 1 или sin 12 sin 2 sin 2 1 0, 1 2 12 sin 1 sin 2 sin 0. 2 Решением arcsin 1 3 этого . A D arcsin 2 уравнения является Таким 1 3 , B C arcsin sin 1 3 , откуда образом, 1 3 . Задача 12. В угол вписаны три окружности – малая, средняя и большая. Большая окружность проходит через центр средней, а средняя через центр малой. Определить радиусы средней и большой окружностей, если радиус меньшей равен r и расстояние ее центра от вершины угла равно а. Решение О1, О2, О3 – центры окружностей, о которых говорится в условии задачи, вписанных в угол ВАС, О1А = а. E, F, K – соответственно точки касания малой, средней и большой окружностей со стороной АС угла. Тогда О1Е = r, О1Е АС, О2F АС, О3K АС и Δ АО1Е Δ АО2F Δ АО3K. Пусть х – радиус средней, у – радиус большой окружности. Тогда О2О1 = О2F = х, О2О3 = О3K = у. Из подобия Δ АО1Е и Δ АО2F следует, что АО1 АО 2 a a x ar ; ; x . О1 Е О2 F r x ar Из подобия Δ АО1Е и Δ АО3K следует, что ar r a АО1 АО3 a a x y r a x a2r ar . ; ; y О1 Е О3 F r y ar ar a r 2 a2r ar Ответ: ; . a r a r 2 Задача 14. Круг разделен диаметром на два полукруга. В один из них вписаны два новых полукруга, опирающихся на радиус данного круга, как на свой диаметр. В криволинейную фигуру, ограниченную контурами этих трех полукругов. вписан круг. Во сколько раз его площадь меньше площади данного круга? Решение О1 – центр данного круга, АВ – его диаметр, О2 – середина АО1 – центр одного полукруга, О3 – середина ВО1 – центр второго полукруга, О4 – центр круга, вписанного в криволинейную фигуру, о которой говорится в условии задачи. Пусть R – радиус круга с центром О1, S1 – его площадь, r – радиус круга с центром О4, S2 – его площадь. Тогда О1О2 О1О3 R , 2 О2 О4 О3 О4 R r, 2 O1O4 R r. В Δ О2О4О3 О2О4 = О3О4, О1 – середина О2О3. Следовательно, О2О4 О2О3 и О2О42 = О1О22 + О1О42. 2 2 R R 2 r R r ; 2 2 Тогда R 2 3Rr; R 3r. S1 R 2 9. S2 r 2 Ответ: в 9 раз. Задача 15. Основания двух правильных треугольников со сторонами а и 3а лежат на одной и той же прямой. Треугольники расположены по разные стороны от прямой и не имеют общих точек, а расстояние между ближайшими концами их оснований равно 2а. Найти расстояние между вершинами треугольников. Решение Правильные В 2а К аа А треугольники АВС и DFE – треугольники, о D Е 3а С которых говорится в условии задачи, АС = а, DE = 3а, CD = 2а. Так как BCD = FDC = 120o, F то ВС║DF. К – точка пересечения прямой DF и прямой, проходящей через точку В параллельно АС. Следовательно, BKDC – параллелограмм, ВК = CD = 2а, KD = ВС = а, KF = KD + DF = 4a, BKD = CDF = 120o. Из ΔBKF: BF BK 2 KF 2 2 BK KF cos BKF 4a 2 16a 2 2 2a 4a cos 120 2a 7. Ответ: 2a 7. Задача 16. Доказать, что для всякого треугольника АВС справедливо неравенство cos A + cos B + cos C 3 . 2 Решение На стороне треугольника построим единичные векторы е1 , е 2 , е3 . Суммой этих векторов В е2 является некоторый вектор d , т.е. е1 е 2 е3 d . Возведем обе части е1 равенства в квадрат: е3 С А е12 е2 2 е3 2 2е1е2 2е1е3 d 2 , или 2 1 1 1 2 cos B 2 cos C 2 cos A d . 2 Так как d 0 , то 3 2 cos B 2 cos C 2 cos A 0 , откуда 3 cos A cos B cos C . 2 Список литературы. 1. Сборник задач по математике для поступающих во втузы. Учебное пособие. Под. ред. М.И. Сканави. – М.: Высш. шк., 1993 г. 2. Математические олимпиады школьников. И.С. Петраков. – М.: Просвещение, 1981 г. 3. Геометрия для 10-11 классов . Учебное пособие для учащихся гимназий, лицеев, школ (классов) с углубленным изучением математики. Е.В. Потоскуев – Тольятти.: Издательство Фонда «Развитие через образование», 2000 год. 4. Решение конкурсных задач по математике. Н.Н. Поляк, А.Г. Мерзляк. – М: Инфолайн, 1995 год.