ДЕМО-ВЕРСИЯ Комплект заданий для контрольной работы

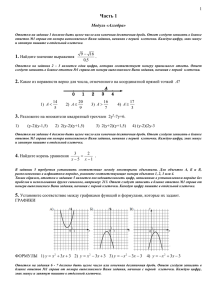
ДЕМО-ВЕРСИЯ
Комплект заданий для контрольной работы
по математике,
8 класс
Тема контрольной работы.
1. Диагностическая итоговая работа
Критерии оценки: варианты работы состоит из 2-х частей и 2- модулей (алгебра, геометрия). Задания
первой части выполняются с краткой записью ответа. Задание второй части предусматривают полное
решение с записью ответа и расположены по нарастанию сложности. Данная работа рассчитана на 90
минут.
Оценка
«Отлично»
«Хорошо»
«Удовлетворительно»
«Неудовлетворительно»
За что выставляется
Ставится при выполнении
Ставится при выполнении
Ставится при выполнении
Ставится при выполнении
23-38 баллов
16-22 баллов
8-15 баллов
0-7 баллов
Вариант № 1.
Часть 1.
Модуль «Алгебра»
Ответом на задания В1–В5 должно быть целое число или конечная десятичная дробь. Ответ следует записать в
бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак
минус и запятую пишите в отдельной клеточке. При выполнении заданий А1–А3 в бланке ответов АВ под кодом
выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами
ответа.
B 1. Найдите значение выражения
.
A 1. На координатной прямой отмечены числа , , .
Какое из следующих утверждений неверно?
1)
2)
3)
4)
.
A 2. Расположите в порядке возрастания числа:
1)
2)
3)
В 2. Решите уравнение
;
; 5,5.
4)
. В ответ запишите наибольший из корней.
B 3. На рисунке изображены графики функций вида у = kх + b. Установите соответствие между графиками и знаками коэффициентов k и b.
А Б В
1) k < 0, b < 02) k > 0, b > 03) k < 0, b > 04) k > 0, b < 0
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
B 4. Решите систему уравнений
. В ответ укажите только значение х.
B 5. Упростите выражение
, найдите его значение при
ченное число.
A 3. На каком рисунке изображено множество решений неравенства
1)
2)
3)
. В ответ запишите полу-
4)
Модуль «Геометрия»
Ответом на задания В6–В10 должно быть целое число или конечная десятичная дробь. Ответ следует записать в
бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак
минус и запятую пишите в отдельной клеточке.
B 6. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АСобразует с основанием ВС и
боковой стороной АВ углы, равные 30° и 50° соответственно.
B 7. Точки
и
делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину
центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
B 8. Найдите площадь параллелограмма, изображённого на рисунке.
B 9. На рисунке изображена трапеция
. Используя рисунок, найдите
.
B 10. Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
В ответе укажите последовательность номеров, выбранных вами утверждений, в порядке
возрастания, без пробелов и знаков препинания.
Модуль «Реальная математика»
Ответом на задания В11–В16 должно быть целое число или конечная десятичная дробь. Ответ следует записать в
бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак
минус и запятую пишите в отдельной клеточке. При выполнении задания А4 в бланке ответов АВ под кодом
выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами
ответа.
A 4. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов
детьми от 1 года до 14 лет и взрослыми.
Какой вывод о суточном потреблении углеводов 12-летним мальчиком можно сделать, если по подсчётам
диетолога в среднем за сутки он потребляет 359 г углеводов?
1) Потребление в норме.
2) Потребление выше рекомендуемой нормы.
3) Потребление ниже рекомендуемой нормы.
3) В таблице недостаточно данных.
B 11. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.
B 12. Чашка, которая стоила 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?
B 13. От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
B 14. На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового
эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за последние два часа программы по сравнению с первыми двумя часами этой программы.
В 15. Бросили два игральных кубика, при этом сумма выпавших очков не превосходит 9. Сколько таких
вариантов существует?
B 16. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура
по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.
Часть 2
При выполнении заданий этой части в бланк ответов С под кодом выполняемого вами задания (С1–С6)
занесите полное обоснованное решение и ответ.
Модуль «Алгебра»
C 1. Сократите дробь
C 2. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из
Вв А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и
сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в
8 км от пункта В.
C 3. Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины и
постройте ее график.
Модуль «Геометрия»
C 4. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности,
заключённая внутри этого угла, равна 100°.
C 5. В параллелограмме KLMN точка Е — середина стороны LM. Известно, что EK = EN. Докажите, что
данный параллелограмм — прямоугольник.
C 6. Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая
сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.