КДР 8-3
реклама

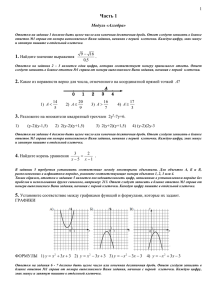
Вариант № 1. Часть 1. Модуль «Алгебра» Ответом на задания В1–В5 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. При выполнении заданий А1–А3 в бланке ответов АВ под кодом выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа. B 1. Найдите значение выражения . A 1. На координатной прямой отмечены числа , , . Какое из следующих утверждений неверно? 1) 2) 3) 4) . A 2. Расположите в порядке возрастания числа: 1) 2) 3) В 2. Решите уравнение ; ; 5,5. 4) . В ответ запишите наибольший из корней. B 3. На рисунке изображены графики функций вида у = kх + b. Установите соответствие между графиками и знаками коэффициентов k и b. А Б В 1) k < 0, b < 0 2) k > 0, b > 0 3) k < 0, b > 0 4) k > 0, b < 0 Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке. B 4. Решите систему уравнений . В ответ укажите только значение х. B 5. Упростите выражение , найдите его значение при запишите полученное число. A 3. На каком рисунке изображено множество решений неравенства 1) 2) 1 3) . В ответ 4) Модуль «Геометрия» Ответом на задания В6–В10 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. B 6. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно. B 7. Точки и делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах. B 8. Найдите площадь параллелограмма, изображённого на рисунке. B 9. На рисунке изображена трапеция . Используя рисунок, найдите . B 10. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы равны. 3) Любая биссектриса равнобедренного треугольника является его медианой. В ответе укажите последовательность номеров, выбранных вами утверждений, в порядке возрастания, без пробелов и знаков препинания. Модуль «Реальная математика» Ответом на задания В11–В16 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. При выполнении задания А4 в бланке ответов АВ под кодом выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа. A 4. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми. 2 Какой вывод о суточном потреблении углеводов 12-летним мальчиком можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 359 г углеводов? 1) Потребление в норме. 2) Потребление выше рекомендуемой нормы. 3) Потребление ниже рекомендуемой нормы. 3) В таблице недостаточно данных. B 11. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник. B 12. Чашка, которая стоила 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить? B 13. От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. B 14. На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за последние два часа программы по сравнению с первыми двумя часами этой программы. В 15. Бросили два игральных кубика, при этом сумма выпавших очков не превосходит 9. Сколько таких вариантов существует? B 16. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых. 3 Часть 2 При выполнении заданий этой части в бланк ответов С под кодом выполняемого вами задания (С1–С6) занесите полное обоснованное решение и ответ. Модуль «Алгебра» C 1. Сократите дробь C 2. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В. C 3. Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины и постройте ее график. Модуль «Геометрия» C 4. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 100°. C 5. В параллелограмме KLMN точка Е — середина стороны LM. Известно, что EK = EN. Докажите, что данный параллелограмм — прямоугольник. C 6. Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM. 4 Вариант № 2. Часть 1. Модуль «Алгебра» Ответом на задания В1–В5 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. При выполнении заданий А1–А3 в бланке ответов АВ под кодом выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа. B 1. Найдите значение выражения . A 1. На координатной прямой отмечены числа . Какое из следующих утверждений неверно? 1) 2) 3) 4) . А 2. В каком случае числа расположены в порядке возрастания? 1) 2) 3) В2. Решите уравнение 4) . В ответе укажите наименьший из корней. B 3. Установите соответствие между графиками функций и формулами, которые их задают. А Б В 1) 2) 3) 4) Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке B 4. Решите систему уравнений . В ответ укажите только значение у. B 5. Упростите выражение , найдите его значение при запишите полученное число. А 3. На каком рисунке изображено множество решений неравенства 5 . В ответ ? 1) 2) 3) 4) Модуль «Геометрия» Ответом на задания В6–В10 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке . B 6. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно. B 7. Точки и делят окружность на две дуги, длины которых относятся как 5:7. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах. B 8. Найдите площадь трапеции, изображённой на рисунке. B 9. На рисунке изображен параллелограмм . . Используя рисунок, найдите B 10. Укажите номера верных утверждений. 1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части. 2) В любом прямоугольнике диагонали взаимно перпендикулярны. 3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. В ответе укажите последовательность номеров, выбранных вами утверждений, в порядке возрастания, без пробелов и знаков препинания. Модуль «Реальная математика» Ответом на задания В11–В16 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. При выполнении задания А4 в бланке ответов АВ под кодом выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа. A 4 . Дорожный знак, изображённый на рисунке, называется «Ограничение высоты». Его устанавливают перед мостами, тоннелями и прочими сооружениями, чтобы запретить проезд транспортного средства, габариты которого (с грузом или без груза) превышают установленную высоту. 6 Какому из данных транспортных средств этот знак запрещает проезд? 1) молоковозу высотой 3770 мм 2) пожарному автомобилю высотой 3400 мм 3) автотопливозаправщику высотой 2900 мм 4) автоцистерне высотой 3350 мм B 11. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления во вторник в 6 часов утра. B 12. Альбом, который стоил 120 рублей, продаётся с 25%-ой скидкой. При покупке 5 таких альбомов покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить? B 13. От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода. B 14. Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме. Определите по диаграмме, значков какого цвета было продано больше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета? 1) 20 2) 30 3) 40 4) 50 В 15. Бросили два игральных кубика, при этом сумма выпавших очков более 8. Сколько таких вариантов существует? B 16. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует 111° по шкале Цельсия? 7 Часть 2 При выполнении заданий этой части в бланк ответов С под кодом выполняемого вами задания (С1–С6) занесите полное обоснованное решение и ответ. Модуль «Алгебра» C 1. Сократите дробь C 2. Из пунктов А и В, расстояние между которыми 19 км, одновременно навстречу друг другу вышли два туриста и встретились в 10 км от В. Турист, шедший из А, сделал в пути получасовую остановку. Найдите скорость туриста, шедшего из В, если известно, что он шёл со скоростью, на 1 км/ч меньшей, чем турист, шедший из А. C 3. Парабола проходит через точки A(0; 6), B(6; –6), C(1; 9). Найдите координаты её вершины и постройте ее график. Модуль «Геометрия» C 4. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8. C 5. На стороне треугольника отмечены точки и что если , то треугольник АВС - равнобедренный. так, что . Докажите, C 6. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен . Найдите радиус вписанной окружности треугольника ABC. Вариант № 3. Часть 1. 8 Модуль «Алгебра» Ответом на задания В1–В5 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. При выполнении заданий А1–А3 в бланке ответов АВ под кодом выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа. B 1. Найдите значение выражения A 1. На координатной прямой отмечены числа a и b. Какое из следующих неравенств верно? 1) 2) 3) А 2. В каком случае числа 1) 2) 4) . и 5 расположены в порядке убывания? 3) B 2. Решите уравнение 4) . В ответ запишите наибольший из корней. B 3. На рисунке изображены графики функций вида между знаками коэффициентов и и графиками. А) Б) В) . Установите соответствие А Б В Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке B 4. Решите систему уравнений . В ответ укажите только значение у. B 5. Упростите выражение и найдите его значение при вете запишите найденное значение. A 3. На каком рисунке изображено множество решений неравенства 1) 2) 3) 4) Модуль «Геометрия» 9 . В от? Ответом на задания В6–В10 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке . B 6. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно. B 7. Точки и делят окружность на две дуги, длины которых относятся как 7:29. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах. B 8. Найдите площадь параллелограмма, изображённого на рисун- ке. B 9. На рисунке изображен ромб . Используя рисунок, найдите . B 10. Укажите номера верных утверждений. 1) Если угол острый, то смежный с ним угол также является острым. 2) Диагонали квадрата взаимно перпендикулярны. 3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности. В ответе укажите последовательность номеров, выбранных вами утверждений, в порядке возрастания, без пробелов и знаков препинания. Модуль «Реальная математика» Ответом на задания В11–В16 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. При выполнении задания А4 в бланке ответов АВ под кодом выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа. A 4. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми. Вещество Дети от 1 года до 14 лет Мужчины Женщины Жиры 40−97 70−154 60−102 Белки 36−87 65−117 58−87 Углеводы 170−420 257−586 10 Какой вывод о суточном потреблении жиров 10-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 102 г жиров? 1) Потребление в норме. 2) Потребление выше рекомендуемой нормы. 3) Потребление ниже рекомендуемой нормы. 4) В таблице недостаточно данных. B 11. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмосферного давления во вторник. B 12. Чайник, который стоил 800 рублей, продаётся с 5%-ой скидкой. При покупке этого чайника покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить? В 13. От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. B 14. На диаграмме представлены некоторые из крупнейших по численности населения стран мира. Численность населения какого государства примерно в 6 раз меньше численности населения Индии? В ответе напишите численность населения этой страны в млн чел. В 15. Бросили два игральных кубика, при этом сумма выпавших очков не менее 5. Сколько таких вариантов существует? B 16. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 158° по шкале Фаренгейта? Часть 2 При выполнении заданий этой части в бланк ответов С под кодом выполняемого вами 11 задания (С1–С6) занесите полное обоснованное решение и ответ. Модуль «Алгебра» C 1. Сократите дробь C 2. Из пунктов А и В, расстояние между которыми 27 км, вышли одновременно навстречу друг другу два туриста и встретились в 12 км от В. Турист, шедший из А, сделал в пути получасовую остановку. Найдите скорость туриста, шедшего из В, если известно, что он шёл со скоростью, на 2 км/ч меньшей, чем первый турист. C 3. Парабола проходит через точки K(0; –5), L(4; 3), M(–3; 10). Найдите координаты её вершины и постройте ее график. Модуль «Геометрия» C 4. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°. C 5. На медиане то . треугольника отмечена точка . Докажите, что если C 6. Площадь треугольника ABC равна 80. Биссектриса AD пересекает медиану BK в точке E, при этом BD:CD=1:3. Найдите площадь четырехугольника EDCK. Вариант № 4. Часть 1. 12 , Модуль «Алгебра» Ответом на задания В1–В5 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. При выполнении заданий А1–А3 в бланке ответов АВ под кодом выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа. B 1. Найдите значение выражения A 1. На координатной прямой отмечены числа a и b. Какое из следующих неравенств неверно? 1) 2) 3) 4) А2. В каком случае числа расположены в порядке убывания? 1) 2) 3) B 2. Решите уравнение 4) . В ответе укажите наименьший из корней. B 3. Установите соответствие между функциями и их графиками. А) Б) В) А Б В Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке B 4. Решите систему уравнений . В ответ укажите только значение х. B 5. Упростите выражение и найдите его значение при A 3. На каком рисунке изображено множество решений неравенства 1) 2) 3) Модуль «Геометрия» 13 . ? 4) Ответом на задания В6–В10 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. B 6. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием BC и боковой стороной CD углы, равные 30° и 105° соответственно. B 7. Точки и делят окружность на две дуги, длины которых относятся как 13:23. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах. B 8. Найдите площадь трапеции, изображённой на рисунке. B 9. Найдите синус острого угла трапеции, изображённой на рисунке. B 10. Укажите номера верных утверждений. 1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны. 2) Сумма смежных углов равна 180°. 3) Любая высота равнобедренного треугольника является его биссектрисой. В ответе укажите последовательность номеров, выбранных вами утверждений, в порядке возрастания, без пробелов и знаков препинания. Модуль «Реальная математика» Ответом на задания В11–В16 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланке ответов АВ справа от номера выполняемого вами задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. При выполнении задания А4 в бланке ответов АВ под кодом выполняемого вами задания поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа. А 4. Дорожный знак, изображённый на рисунке, называется «Ограничение длины». Его устанавливают там, где запрещён проезд транспортного средства, габариты которого (с грузом или без груза) превышают установленную длину. 14 Какому из данных транспортных средств этот знак запрещает проезд? 1) бензовозу длиной 7600 мм 2) автомобилю Газель длиной 6330 мм 3) автотопливозаправщику длиной 10 200 мм 4) автоцистерне длиной 8250 мм B 11. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду. B 12. Набор полотенец, который стоил 200 рублей, продаётся с 3%-й скидкой. При покупке этого набора покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить? B 13. От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода. B 14 № 316379. Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме. Определите по диаграмме, значков какого цвета было продано меньше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета? 1) 5 2) 10 3) 15 4) 20 В 15. Бросили два игральных кубика, при этом сумма выпавших очков менее 7. Сколько таких вариантов существует? В 16. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта ( °F) пользуются формулой , где — градусы Цельсия, — градусы Фа15 ренгейта. Какая температура (в градусах) по шкале Фаренгейта соответствует 20° по шкале Цельсия? Часть 2 При выполнении заданий этой части в бланк ответов С под кодом выполняемого вами задания (С1–С6) занесите полное обоснованное решение и ответ. Модуль «Алгебра» C 1. Сократите дробь C 2. Из пункта А в пункт В, расстояние между которыми 34 км, выехал велосипедист. Одновременно с ним из В в А вышел пешеход. Велосипедист ехал со скоростью, на 8 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 24 км от пункта А. С 3. Парабола проходит через точки K(0; –2), L(4; 6), M(1; 3). Найдите координаты её вершины и постройте ее график. Модуль «Геометрия» C 4. Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8. C 5. В параллелограмме проведены биссектрисы противоположных углов. Докажите, что отрезки биссектрис, заключенные внутри параллелограмма, равны. C 6. Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC. 16