Методика преподавания темы

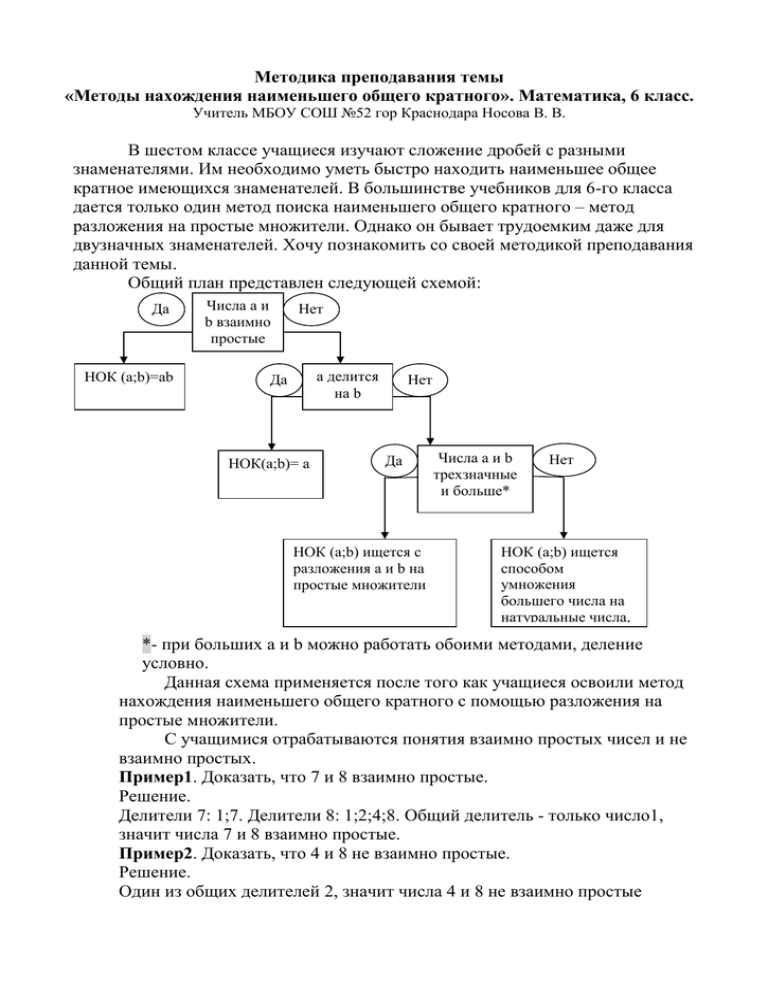
Методика преподавания темы
«Методы нахождения наименьшего общего кратного». Математика, 6 класс.
Учитель МБОУ СОШ №52 гор Краснодара Носова В. В.
В шестом классе учащиеся изучают сложение дробей с разными
знаменателями. Им необходимо уметь быстро находить наименьшее общее
кратное имеющихся знаменателей. В большинстве учебников для 6-го класса
дается только один метод поиска наименьшего общего кратного – метод
разложения на простые множители. Однако он бывает трудоемким даже для
двузначных знаменателей. Хочу познакомить со своей методикой преподавания
данной темы.
Общий план представлен следующей схемой:
Да
НОК (а;b)=аb
Числа а и
b взаимно
простые
Нет
т
а делится
на b
Да
НОК(а;b)= а
Нет
Да
НОК (а;b) ищется с
разложения а и b на
простые множители
Числа а и b
трехзначные
и больше*
Нет
НОК (а;b) ищется
способом
умножения
большего числа на
натуральные числа,
начиная с 2
*- при больших а и b можно работать обоими методами, деление
условно.
Данная схема применяется после того как учащиеся освоили метод
нахождения наименьшего общего кратного с помощью разложения на
простые множители.
С учащимися отрабатываются понятия взаимно простых чисел и не
взаимно простых.
Пример1. Доказать, что 7 и 8 взаимно простые.
Решение.
Делители 7: 1;7. Делители 8: 1;2;4;8. Общий делитель - только число1,
значит числа 7 и 8 взаимно простые.
Пример2. Доказать, что 4 и 8 не взаимно простые.
Решение.
Один из общих делителей 2, значит числа 4 и 8 не взаимно простые
Учащиеся приводят свои примеры взаимно простых и не взаимно
простых чисел, после чего даются задания на распознавание взаимно
простых чисел. Опыт показывает, что после такой работы учащиеся легко
определяют взаимную простоту знаменателей дробей.
Рассмотрим нахождение наименьшего общего кратного способом
умножения большего числа на натуральные числа.
Пример3. Найти НОК(20;15).
Будем последовательно умножать большее число 30 на натуральные
числа, начиная с 2:
20×2=40, 40 не делится на 15;
20×3=60, 60 делится на 15, это и есть НОК(20;15)
Ответ: НОК(20;15)=60
Пример4. Найти НОК(12;15).
Будем последовательно умножать большее число 15 на натуральные
числа, начиная с 2:
15×2=30, 30 не делится на 12;
15×3=45, 45 не делится на 12;
15×4=60, 60 делится на 12, это и есть НОК(12;15)
Ответ: НОК(12;15)=60.
Надо объяснить ученикам, что это не новый метод нахождения
наименьшего общего кратного, а частный случай метода разложения
на простые множители, где одно из чисел умножается на некий
натуральный множитель, просто здесь он находится подбором.
Разберем примеры на применение данной схемы.
Пример5. Найти НОК (13;8).
Решение. Числа 13 и 8 взаимно простые, значит НОК (13;8)= 13×8=104.
Пример6. Найти НОК (45;15)
Решение. 1)Числа 45 и 15 не взаимно простые, так как один из общих
делителей 5.
2) Число 45 делится нацело на 15, значит НОК (45;15)=45.
Пример7. Найти НОК (12;8)
Решение. 1)Числа 12 и 8 не взаимно простые, так как один из общих
делителей 2.
2)Число 12 не делится нацело на 8.
3) Числа 12 и 8 не трехзначные, значит, будем искать
наименьшее общее кратное способом умножения большего числа на
натуральные числа, начиная с 2.
12×2=24, 24 делится на 8, значит, НОК (12;8)=24.
Пример8.Найти НОК (124;186).
Решение. 1)Числа 124 и 186 не взаимно простые, так как один из общих
делителей 2.
2)Число 186 не делится нацело на 124.
3) Числа 124 и 186 трехзначные, значит, будем искать
наименьшее общее кратное методом разложения на простые множители.
124 2
62 2
31 31
1
186 2
93 3
31 31
1
124=2×2×31
186=2×3×31
НОК (124;186)= 2×2×31×3=124×3=372.
Литература:
1. Бунимович Е.А., Дорофеев Г.В., Суворова С.Б. и др. «Математика,
6 кл.», издательство «Просвещение», 2012;
2. Виленкин Н. Я. и др. «Математика 6 кл.» издательство
«Мнемозина», 2012;
3. Зубарева И. И., Мордкович А. Г. «Математика
6 кл.»
издательство «Мнемозина», 2012;