Случайные величины.

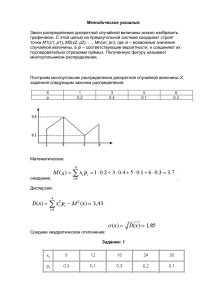
Случайные величины.
Параграф №1. Понятие случайной величины
В предыдущем разделе рассматривались случайные события, которые могут
характеризоваться, как качественная оценка случайного результата опыта. Однако
результат испытания может характеризоваться и количественно. Количественной
характеристикой случайного результата является случайная величина.
Определение №1: Случайная величина – величина, которая в результате опыта может
принимать то или иное значение, причѐм заранее неизвестно какое.
Случайные величины бывают непрерывными и дискретными и обозначаются как X ,
Y , Z и так далее. Их численные значения обозначаются, как x , y , z и так далее.
Определение №2: Дискретная случайная величина – случайная величина, возможные
значения которой составляют счетное множество (то есть множество, элементы которого
могут быть занумерованы).
Например, оценка студента на экзамене, количество студентов, присутствующих на
лекции и так далее.
Определение №3: Непрерывная случайная величина – случайная величина, возможные
значения которой непрерывно заполняют некоторый интервал (конечный или
бесконечный).
Например, дальность броска ядра на соревнованиях, время безотказной работы
устройства.
Параграф №2. Закон распределения вероятностей дискретной случайной величины.
Для полной характеристики случайной величины не достаточно указывать только еѐ
возможные значения. Необходимо также учитывать то, как часто появляется то или иное
значение случайной величины при повторении опытов. Это достигается с помощью
закона распределения вероятностей случайной величины, который устанавливает связь
между возможными значениями случайной величины и соответсвующими вероятностями.
Пусть в результате опыта случайная величина X принимает некоторое своѐ значение
x i , то есть происходит событие X  xi .
Все события, состоящие в том, что X  x1 , X  x2 ,…, X  xn (1)
являются несовместными и составляют полную группу.
Предположим, что известны вероятности этих событий:
P X  x1   p1 ,
P X  x2   p2 ,…, P X  xn   pn (2).
Так как события (1) составляют полную группу, то сумма вероятностей всех
возможных значений случайной величины X равна единице, то есть
n
p
i 1
i
 1 (3).
Одной из простейших форм задания закона распределения вероятностей для
дискретной случайной величины является таблица, первая строка которой содержит
возможные значения случайной величины, а вторая - соответствующие им вероятности.
X x1 x 2 x3 … x n
p1 p 2 p 3 … p n
Такая таблица называется рядом распределения.
Кроме этого используется также графическое представление, когда возможное
значение случайной величины откладывается на ось абсцисс, а соответствующие значения
вероятностей на оси ординат.
P
1
P
p3
Многоугольник распределения
p4
p2
p1
x1 x2
x3
x4
X
Для
наглядности
точки
соединяются между собой, однако
необходимо помнить, что эти линии
носят чисто условный характер, так
как
в
промежутках
случайная
величина не принимает никаких
значений.
Примечание: Согласно свойству
(3) сумма вероятностей во второй
строке ряда распределения всегда
равна единице, так же как и сумма
ординат многоугольника распределения.
Параграф 3. Функция распределения.
Закон распределения вероятностей устанавливает связь между возможными
значениями случайной величины и соответствующими им вероятностями. Одной из форм
такого закона является ряд распределения, однако он не может быть использован для
описания непрерывной случайной величины, так как она имеет бесчисленное множество
возможных значений. Поэтому используется более универсальная форма этого закона –
функция распределения. Функция распределения может использоваться как для
дискретной, так и для непрерывной случайной величины.
Определение №1: Функция распределения F x  - закон, задающий вероятность
выполнения условия X  x , то есть F x   P X  x  .
С геометрической точки зрения, если рассматривать
x
x случайную величину X как случайную точку, падающую на
числовую ось случайным образом, то F x  показывает
вероятность того, что случайная точка упадѐт в результате опыта на ось левее точки с
абсциссой x .
Рассмотрим дискретную случайную величину: P X  0  p0 , P X  1  p1 ,
P X  2  p2 , P X  3  p3 , P X  4  p4 . Из графика видно, что функция
распределения для дискретной случайной величины терпит разрыв в точках еѐ возможных
значений, причѐм величина скачка функции равна
F x 
вероятности соответствующего значения случайной
величины.
p3
Свойства функции распределения.
1. Функция
распределения
является
p2
положительной, лежащей в интервале от нуля
до единицы. Доказательство очевидно из
p1
определения функции распределения.
F    0 , F   1 . Доказательство очевидно
2.
p0
из геометрического представления функции
x
распределения.
3. Вероятность попадания случайной величины X в интервал [ ;  ) равна
разности значений функции распределения на концах интервала:
P  X     F    F   (1).
Доказательство: Введѐм следующие случайные события: событие A - X   ,
событие B - X   , событие C -   X   . Очевидно, что событие A
представляет собой сумму событий B и C , то есть A  B  C . Так как события A ,
B и C несовместны, то P A  PB  PC 
2
P A  P X     F  
PB   P X     F  
F    F    P  X   
P  X     F    F  
4. Функция распределения является неубывающей, то есть при   
выполняется неравенство F    F   . Доказательство очевидно из третьего
свойства.
Параграф №5. Плотность распределения.
К сожалению функция распределения не отражает того с какой вероятностью
случайная величина принимает то или иное своѐ значение.
Определение №1: Плотность распределения случайной величины - предел отношения
вероятности попадания случайной величины на элементарный интервал x; x  x  к
длине этого интервала x , когда последняя стремится к нулю x  0 , то есть
Px  X  x  x 
(1).
f x   lim
x 0
x
F x  x   F x 
F
Согласно свойству (3) параграфа 3: f x   lim
 lim
 F x  , то
x 0
x 0 x
x
есть f x   F x  (2).
Если же случайная величина может
f x 
принимать значения только в пределах
Кривая распределения
ограниченного отрезка a; b , то вне этого
отрезка f x   0 .
a
x
b
Свойства плотности распределения.
1. Плотность распределения является неотрицательной функцией, то есть
f x   0 .
Доказательство. Согласно формуле (2) плотность распределения является
производной от неубывающей функции распределения.
2. Функция распределения равна несобственному интегралу от плотности
распределения, то есть F x  
x
 f t dt
(3).

Доказательство. Из формулы (2) имеем: dF x   f x dx
3
x
x
 dF x  
 f t dt


F  x   
x
 f t dt
x

x
F  x   F    
 f t dt

F     0
F x  
f x 
F x 
x
x
x
 f x dx

3. Вероятность попадания случайной величины на интервал  ;   равна
определѐнному интегралу от плотности распределения на данном интервале, то

есть P  X      f x dx (4).

Доказательство. Из формулы (2) имеем dF x   f x dx


 dF x    f x dx



F  x     f  x dx



F    F     f  x dx


P  X      f  x dx


4.
 f x dx  1 (5).

Доказательство. Рассмотрим формулу (3) параграфа 4, в случае когда x   .
F   

 f x dx

F    1

 f x dx  1

В том случае, когда случайная величина может принимать значения только на
конечном интервале a; b , то (5) принимает вид:
b
 f x dx  1 (5а).
a
Плотность распределения показывает как часто случайная величина принимает своѐ
значение в бесконечно малой окрестности той или иной точки при повторении опытов в
одинаковых условиях.
Параграф №5. Математическое ожидание.
Во многих практических случаях нет необходимости полностью описывать случайную
величину с помощью плотности или функции распределения. Часто бывает достаточно
4
всего двух числовых характеристик, чтобы описать основные особенности данной
случайной величины. Одной из таких числовых характеристик является математическое
ожидание, представляющее собой некоторое среднее значение, вокруг которого
группируются возможные значения случайной величины.
Определение №1: Математическое ожидание для дискретной случайной величины –
сумма произведений возможных значений случайной величины на их соответствующие
n
вероятности, то есть M X   m x  x1 p1  x2 p 2  ...  xn p n   xi pi (1).
i 1
Примечание: В том случае, когда все вероятности возможных значений равны между
1
1 n
собой, то есть p1  p 2  p n  , математическое ожидание принимает вид: m x   xi ,
n
n i 1
то есть в этом случае математическое ожидание равно среднему арифметическому.
Определение №2: Математическое ожидание непрерывной случайной величины –
формула вида M X   m x 

 xf x dx (2).

Если случайная величина может принимать значения только на конечном интервале
a; b , то
b
M x   m x   xf x dx (2а).
a
Механический смысл математического ожидания.
Рассмотрим стержень длиной l , масса которого равна 1. Расположим стержень на
отрезке a; b на оси x . Плотность этого стержня меняется по длине согласно некоторому
закону, который описывается функцией f x  , совпадающей с графиком плотности
распределения. Тогда математическое ожидание будет совпадать с абсциссой центра
тяжести этого стержня.
Свойства математического ожидания.
1. Математическое ожидание константы равно самой константе, то есть
M C   C .
Доказательство. Рассмотрим простейший случай дискретной случайной величины,
которая может принимать всего одно значение с вероятностью равной единице,
тогда M C   C  1  C .
2. Константу можно выносить за знак математического ожидания, то есть
M CX   CM X  .
Доказательство. Для дискретной случайной величины:
n
M CX    Cxi pi 
i 1
n
b
i 1
a
 C  xi pi  CM X  . Для непрерывной случайной величины: M CX   Cxf x dx 
b
 C  xf x dx  cM X .
a
Параграф №6. Дисперсия. Среднее квадратическое отклонение.
Они представляют собой числовые характеристики рассеяния, то есть они показывают,
насколько плотно группируются возможные значения случайной величины вокруг центра
рассеяния, то есть вокруг математического ожидания.
5
Определение №1: Дисперсия случайной величины – математическое ожидание
квадрата отклонения случайной величины от еѐ математического ожидания, то есть
2
DX   M  X  mx  .
Для дискретной случайной величины на основе пятого параграфа верно следующее


n
равенство: DX    xi  m x  pi (1).
2
i 1
Для непрерывной случайной величины: DX  

 x  m  f x dx (2).
2
x

Дисперсия обладает тем недостатком, что она имеет размерность квадрата случайной
величины, поэтому для большей наглядности вводят понятие среднего квадратического
отклонения, совпадающего по размерности со случайной величиной:  x  Dx (3).
Свойства дисперсии.
1. Дисперсия константы равна нулю, то есть DC   0 .


Доказательство. На основе определения дисперсии: DC   M C  M C  . С учѐтом


2
первого свойства пятого параграфа: M C  C   M 0  0 .
2. Константу можно выносить за знак дисперсии во второй степени, то есть
DCX   C 2 DX .

2

Доказательство. DCX   M CX  M CX  . С учѐтом второго свойства пятого

2



параграфа: M CX  CM X   C M  X  M X   C 2 DX  .
3. Дисперсия равна разности математического ожидания квадрата случайной
величины и квадрата математического ожидания, то есть DX   M X 2  mx2 .
2
2
2
 
n
n


Доказательство: Для дискретной величины: DX    xi  m x  pi   xi2 pi 
2
i 1
n
 
n
i 1
 
 2m x  xi pi  m x2  pi  M X 2  2m x2  m x2  M X 2  m x2 .
i 1
i 1


1
b
b
Для непрерывной случайной величины: DX    x  m x  f x dx   x 2 f x dx 
2
a
b
b
b
b
a
 
b
 2 xm x f x dx   m x2 f x dx   x 2 f x dx  2m x  xf x dx  m x2  f x dx  M x 2  m x2 .
a
a
a
a
a



1
Параграф №7. Равномерное распределение.
Случайная величина имеет равномерное распределение на некотором отрезке a; b ,
если в пределах этого отрезка плотность распределения не меняется (то есть все значения
случайной величины внутри этого отрезка равновероятны), а за его пределами равняется
0, при x  a

нулю, то есть f x   C , при a  x  b .
0, при b  x

Так как площадь под кривой распределения всегда равна единице, то C 
1
.
ba
6
x
Найдѐм функцию распределения: F x  


x
x
a
f x 
F x 
dt
t
xa
.


b

a
a

b
b

a
a
a
x
f t dt   f t dt  
1
a
x
b
a
mx
b
x
0, при x  a
x  a

F x   
, при a  x  b
b  a
1, при x  b
b
x
x2
b2  a2
ab
m x   xf  x dx  
dx 


2
ab
2b  a  a 2b  a 
2
a
a
b
b
b  a 
ab 1

2
D x    x  m x  f  x dx    x 
dx 

2  ba
12
a
a
b
b
b  a 2
x 

2
2
ba
12
2 3
Вероятность попадания в интервал, расположенный внутри отрезка  ;  .

P  x     



dx
x
 
f x dx  


ba 
ba
 ba
f x 
1
ba
P
a  
x
b
7
Параграф №8. Экспоненциальное (показательное) распределение.
Экспоненциальный или показательный закон распределения имеет следующий вид:
e  x , при x  0
.
f x   
0, при x  0
Пример: Вероятность безотказной работы прибора.
x
x
x
f x 
F x    f t dt   e t dt  e t  1  e x
0


0
1  e  x , при x  0
F x   
0, при x  0
x
F x 
mx 
1




0
0
 x
 xf x dx   xf x dx   xe dx 
Ux
dU  dx V 
;
x 
1
    lim x  0

x
x  e
   x   e
x Лопиталя);


1  x
1  x  1
1
 x


e
dx


e
d


x


e
 ;
Таким образом m x  .


lim

0

0


2

0
(Правило

2
1
1
1


Dx    x   e x xdx     x   e x dx  2 (Дважды по частям);




0
1
Тогда  x  ;

Таким образом, в показательном распределении математическое ожидание и среднее
квадратичное отклонение равны между собой.
Введем случайную величину Т – длительность времени безотказной работы. Если елемент
начал работать в момент t 0  0 и через время t происходит отказ, то функция
распределения по определению F (t )  P(T  t ) есть вероятность отказа в момент времени t.
Следовательно вероятность противоположного события – безотказной работы за это же
время t – равна R(t )  1  F (t )  e t , где R(t) – называется функцией надежности,
показывающей вероятность безотказной работы за время t.
Rt 
F t 
1
1
t
Вероятность поломки
dV
t
Вероятность
безотказной работы
8
Параграф №9. Нормальное распределение. Закон Гаусса.
Нормальное распределение является самым распространѐнным законом распределения
непрерывной случайной величины, широко используемый так же в инженерной практике.
Пример: При изготовлении втулок на токарном станке, отклонение диаметра втулок
от номинального размера описывается нормальным распределением.
Данный закон проявляется тогда, когда случайная величина X является результатом
действия большого числа факторов, причѐм влияние каждого из них на случайную
величину незначительно, и среди них нельзя выбрать какой-то один доминирующий
фактор.
f x  

1
 x 2
e
 x  mx 2
2 x2
(1),
где m x - математическое ожидание,  x - среднее
f x 
квадратичное отклонение.
1
График
плотности
распределения
называется  2
x
нормальной кривой, или кривой Гаусса.
Свойства графика (кривой Гаусса):
1. Функция (1) является чѐтной, еѐ график
симметричен относительно прямой x  m x .
mx
2. Данная функция имеет экстремум в точке
f x 
1
1
.
x  m x , равный
 x 2
 x 2
3. При
стремящемся
к
плюс\минус
x
бесконечности график функции стремится к
нулю, то есть ось x является горизонтальной
mx1 mx 2
асимптотой.
1
f x 
4. При изменении математического ожидания m x ,
2 2
но при постоянном среднем квадратичном
отклонении
график
функции
смещается
1
относительно оси x , при этом его форма не
4 2
изменяется.
5. При
изменении
среднего
квадратичного
mx
отклонения
но
при
постоянном
x,
математическом ожидании нормальная кривая трансформируется.
Вероятность попадания в интервал  ;   :

P  X      f x dx 

1
x

e
2 
Ввѐдем новую переменную: z 
P(  X   ) 
z1 
1
2
z2
e

z2
2
dz 
z1

2
x
x
 x  mx 2
2 x2
x  mx
1
x
x
dx .
dz 
,
0
z
e
2
/2
dz 
z1
1
x
1
2
dx , тогда
z2
z
e
0
2
/2
dz 
1
2
z2
z
e
0
2
/2
dz 
1
2
z1
e
z2 / 2
0
  mx
  mx
, z2 
x
x
Введѐм функцию Лапласа:
Ф x  
1
2
x
e

z2
2
dz .
0
9
dz,
   mx
Таким образом: P  X     Ф
 x

   mx
  Ф

 x



(2).
Правило трёх сигм.
От математического ожидания вправо и влево
f x 
откладываем 3 x , тогда   mx  3 x ,   mx  3 x . По
формуле (2) находим вероятность попадания в данный
интервал  ;   : P  X     Ф3  Ф 3 .
Так
как
функция
Лапласа
нечѐтная,
то
то
есть
P  X     Ф3  Ф3  2Ф3  0.997 ,
mx 
вероятность оказаться за пределами данного интервала

x
практически равна нулю.
3 3
Правило трѐх сигм: Если непрерывная случайная
величина распределена нормально, то абсолютная величина еѐ отклонения от
математического ожидания не превышает трех сигм, то есть с вероятностью почти в сто
процентов можно записать следующее неравенство: x  mx  3 x .
Параграф №10. Биномиальное распределение.
Биномиальное распределение является самым распространѐнным законом
распределения для дискретной случайной величины.
Дискретная случайная величина X показывает число появления события A в n
независимых испытаниях, проводящихся в одинаковых условиях, при этом вероятность
появления события A в каждом испытании одна и та же и равна p .
Очевидно, что возможные значения случайной величины 0, 1, 2, 3,…, n . Вероятности
каждого из этих возможных значений подсчитываются по формуле Бернулли, которая
nm
имеет следующий вид: Pnm  Cnm p m 1  p   Cnm p m q nm
(1).
Используя формулу (1) можно составить ряд распределения:
0
Pn0
1
Pn1
…
…
2
Pn2
n
Pnn
События, состоящие в различном числе появлений события А в серии из n испытаний,
несовместны и образуют полную группу. Поэтому сумма вероятностей, входящих в ряд
распределения, равна единице, то есть
n
P
m 0
m
n
1
n
C
или
m 0
m
n
p m q nm  1.
Левая часть данного равенства напоминает бином Ньютона
n
q  p n   Cnm p m q nm
(2),
m 0
поэтому данное распределение называется биномиальным.
Математическое ожидание: mx  np
(3).
Доказательство:
По определению математического ожидания:
n
n
m 0
m 0
mx  0  Pn0  1  Pn1  2  Pn2  ...  n  Pnn    mPnm   mCnm p nm q nm
(4)
Продифференцируем формулу бинома (2) по p :
10
n p  q 
n 1
n
  mCnm p m1 q n m . Умножив левую и правую части на
p , получим
m 0
следующее равенство: np p  q 
n 1
n
  mCnm p m q nm (5).
m 0
Так как правые части равенств (4) и (5) равны, то np p  q   mx . Так как p  q  1 ,
следовательно, np  m x .
Таким образом, математическое ожидание числа наступления события в серии
независимых и одинаковых испытаний равно произведению числа испытаний в серии на
вероятность появления события в каждом испытании.
Дисперсия: Dx  npq
(6).
Дважды дифференцируя формулу бинома (2) по р и затем умножая левую и правую
часть полученного равенство на p 2 нетрудно доказать (6).
n 1
Среднее квадратическое отклонение:  x  npq
Параграф №11:
(7).
Распределение Пуассона.
Примером данного распределения дискретной случайной величины является
количество вызовов, приходящих на телефонную станцию за определѐнный промежуток
времени t .
Пусть на оси x точки распределены случайным
x
образом, так что вероятность попадания данного
числа точек на отрезок длиной l зависит только от
длины этого отрезка и не зависит от количества точек на соседних отрезках.
Предполагается, что точки распределены вдоль оси x с одинаковой средней плотностью,
равной  .
Средняя плотность  - среднее количество точек (то есть математическое ожидание
числа точек), приходящихся на единицу длины.
Если мы берѐм отрезок x , то выражение x покажет математическое ожидание
числа точек, приходящихся на отрезок x , то есть M Y   x , где Y - число точек,
приходящихся на отрезок x .
Предположим, что отрезок x настолько мал, что вероятность попадания на него двух
и более точек ничтожна мала. В этом случае вероятность попадания одной точки на x
можно найти по следующей формуле: PY  1  x . Действительно, с одной стороны
M Y   x , с другой стороны M Y   0  PY  0  1  PY  1  2  PY  2  ...  n 

 PY  n   PY  1 , таким образом PY  1  x .



0
0
Предположим, что отрезок l разбили на n маленьких отрезков длиной x 
вероятность попадания одной точки на отрезок x равняется x  
l
, тогда
n
l
, а вероятность
n
l
.
n
Попадание или непопадание точки в каждый из n отрезков можно рассматривать как
результат n независимых опытов. Вероятность того, что из n отрезков точка появляется
ровно в m отрезках вычисляется по формуле Бернулли:
непопадания точки в отрезок x равняется 1  
11
m
nm
l
 l 
(1).
Pnm  C nm    1   
n
 n 
Формула (1) приближѐнно выражает вероятность того, что среди n отрезков одна
точка будет содержаться в m отрезках. Эта вероятность будет тем точнее, чем меньше
длина отрезков x и чем больше их количество n . Переходя к пределу при x  0 и
n   , получим точное значение вероятности того, что на отрезок длиной l попадѐт
ровно m точек: Pm  P X  m , где X - число точек, приходящихся на отрезок l :
Pm  P X  m 
nm
nm
 m  l m 
 l m

 l m l
l
n
!
l




 lim  C n    1     
lim 
1


e , здесь мы




x 0
x 0 n  m ! n m
n
n
m
!
n
m
!






n  
n  


использовали второй замечательный предел. То есть мы получили следующую формулу:

l m l
(2).
Pm 
e
m!
Распределение дискретной случайной величины, описываемое формулой (2),
называется распределением Пуассона.
Математическое ожидание распределения Пуассона, согласно определению средней
плотности, равно: m x  l - математическое ожидание числа точек, приходящихся на
отрезок длиной l .
Дисперсия распределения Пуассона численно равна математическому ожиданию, то
есть Dx  l .
Замечание. Распределение Пуассона может быть приближенно использовано вместо
биномиального распределения в тех случаях, когда математическое ожидание мало
отличается от дисперсии (т.е. когда n велико, а р мало).
12